📦 DNN-SAM: Split-and-Merge DNN Execution for Real-Time Object Detection

Real-time object detection in AVs

There are two key characteristics to consider;

1. Different criticality levels by different portions within each scene image.
   • Other cars or pedestrians nearby on the road.
2. Dynamic variations in the safety-critical portion by scene-by-scene.
   • Varies with the vehicle’s speed/heading and moving objects in its vicinity.

Unfortunately, the existing DNN-based object detection systems are not yet directly applicable to real-time system.

• Use an equal amount of computation for all portions.
• Perform computations sequentially without prioritizing safety-critical portions.
• Cannot achieve both accurate detection and timely response on resource-constrained onboard computing platforms.

Answer: DNN-SAM

DNN-SAM first splits a DNN task into two smaller sub-tasks

• A primary sub-task processing a safety-critical portion only by image cropping.
• A secondary sub-task processing a down-sampled entire image by image scaling.

Then executes them independently, and finally merges their results in to a complete one.

Also, DNN-SAM provides two scheduling algorithms for sub-tasks.

Distinct Benefits

1. It is generally applicable to existing DNN-based object detection systems.
2. It enables to provide different levels of accuracy and responsiveness to sub-tasks.
3. It enables to capture dynamic variations in the size of the safety-critical portion at run-time and adaptively select the scales of optional sub-tasks.

Related works

Dynamic construction of network to meet the timing constraint.

AnytimeNet, NestedNet, dynamic multi-path neural networks.

use an equal amount of computation for all portions of the input image

Real-time scheduling frameworks to schedule multiple DNN tasks.

ApNet, S$^3$DNN, imprecise computation for DNNs, pipelined CPU/GPU scheduling frameworks

not able to prioritize the computation of safety-critical portions of DNN tasks over that of other portions

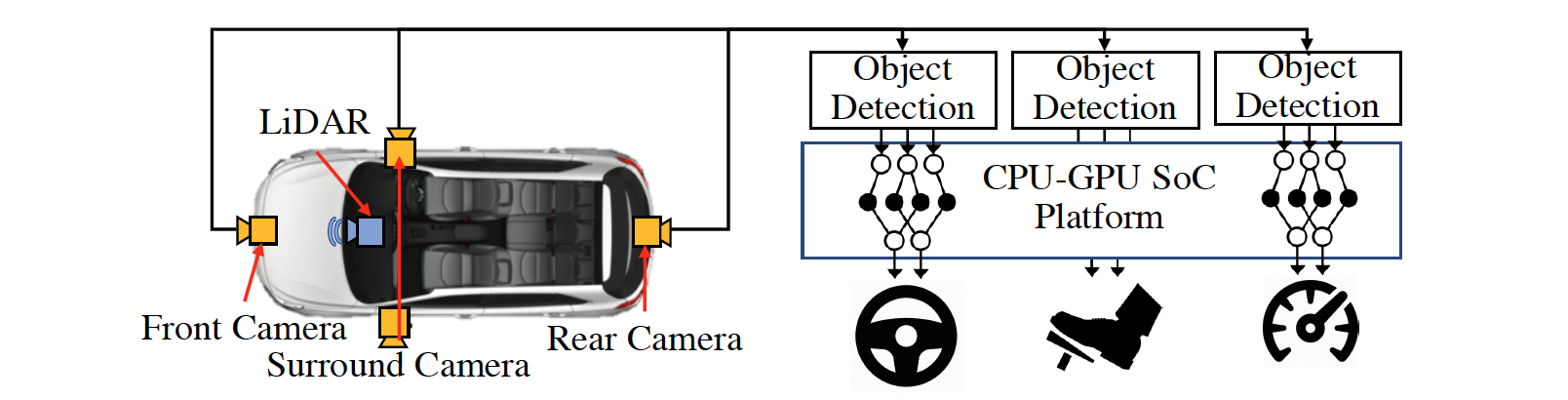
Target System: DNN-based Object Detection

• Multiple cameras + other sensors
• Each vision task is implemented as a periodic task.
• Vision tasks must produce timely inference before their deadlines.

• Safety-critical portion may dynamically vary image-by-image depending on the vehicle’s speed and moving objects in its vicinity: Time-to-collision.
• Each vision tasks must identify a safety-critical portion of an image.

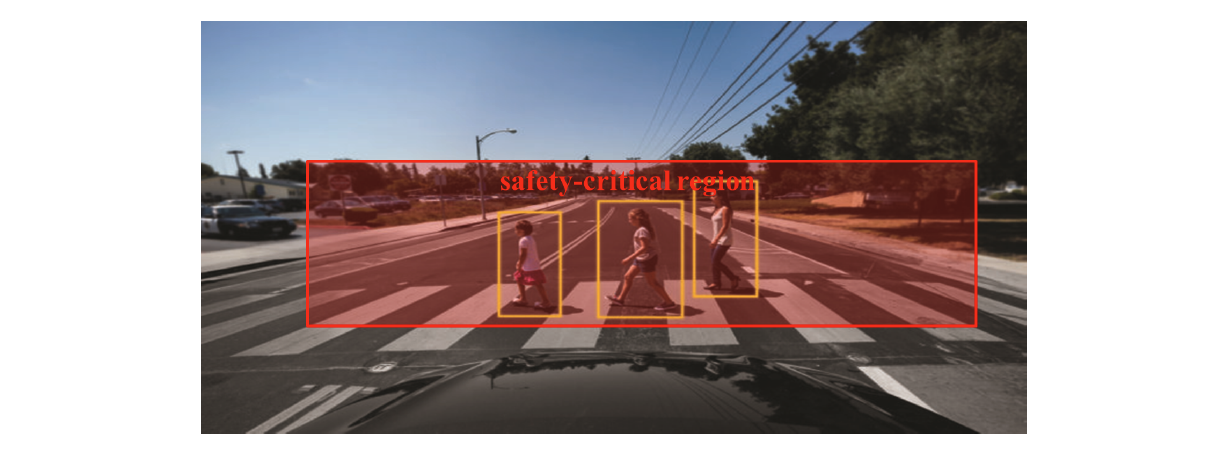
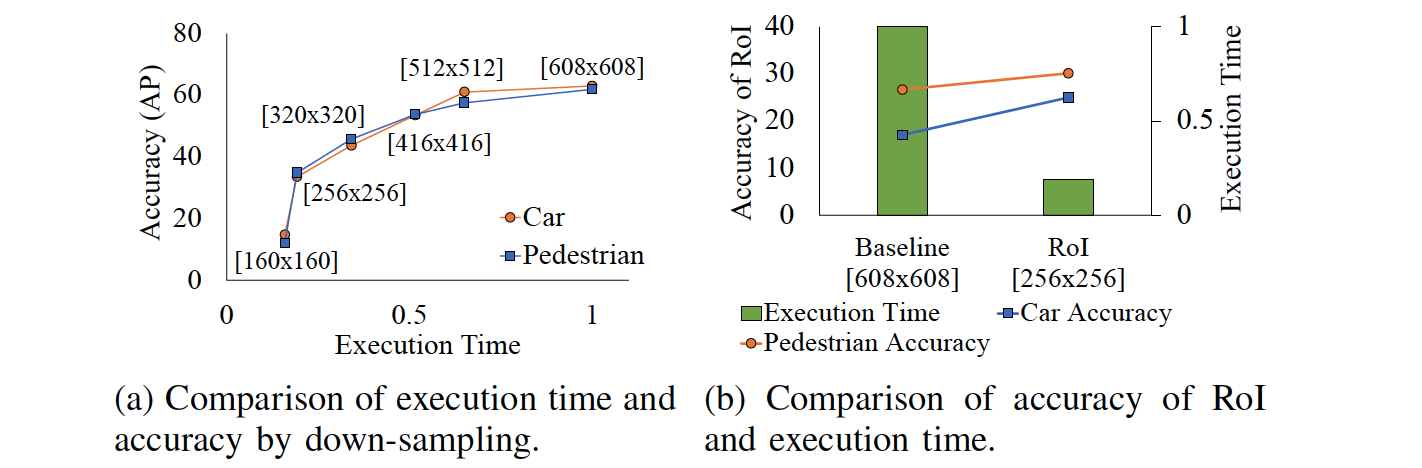
Image Scaling and Cropping

• We can observe a trade-off between execution time and detection accuracy.
• Processing a cropped image can effectively lower the computational workload with no accuracy drop.

DNN-SAM Overview

Core features

• RoI identification
  Extract RoI within each input image using sensor fusion of camera, LiDAR, and IMU.
• Transparent DNN execution
  Enable seamless S&M DNN execution for unmodified DNN models.
• Sub-task scheduling and adaptive scaling
  Automatically orchestrates the execution + monitors available resources to adaptively selects the scales of optional sub-tasks at run-time.

Workflow

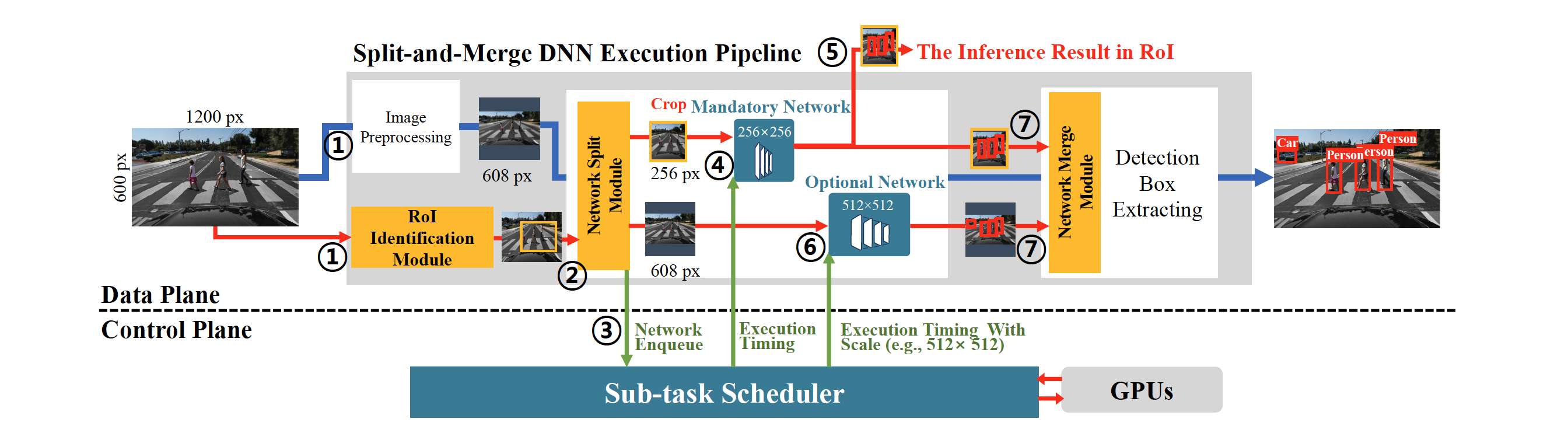
On the other hand, if there is enough spare time before the deadline, an optional sub-task can select an even larger scale than the original input image to improve detection accuracy.

Technical Challenges

C1
How to efficiently identify RoI?

DNN-based approach?

• Usually incurs a high computation.
• Makes timely response of S&M DNN execution difficult.

Sensor fusion approach

• Known to be able to localize objects fast and accurately, and thus is widely used in AVs.

C2
How to decompose the original DNN model into two subtasks in a transparent way without incurring significant space and time overheads and enable use of the output of the mandatory sub-task in advance?

Fork two process?

• Creates 2x the memory footprint.
• Infeasible for resource-constrained computing platforms

Execute sequentially?

• Cannot produce the output of mandatory sub-task in advance withmout modifying the user-level code.

C2
How to decompose the original DNN model into two subtasks in a transparent way without incurring significant space and time overheads and enable use of the output of the mandatory sub-task in advance?

Multi-thread execution

• Enables seamless S&M DNN execution for unmodified DNN models with minimal memory overhead.
• Early use of output of manadory sub-task is possible.

C3
How to merge the outputs of mandatory and optional subtasks by effectively removing duplicated objects?

IoU (Intersection over Union)

• Most widely used evaluation metric to measure the area of overlap.
• Cut-off objects result in low IoU scores.
• DNN-SAM supports a new evaluation metric that can handle those cut-off objects in addition to IoU.

C4
How to schedule sub-tasks while considering system-wide information?

• SOTA ML frameworks employ a simple scheduling principle(FIFO).
• ML frameworks cannot consider system-wide information.

Real-time Scheduler

• Automatically orchestrate the execution of subtasks.
• Adaptively select the scales of optional sub-tasks at run-time subject to available slack to meet the timing requirements.

RoI Identification Module

1. LiDAR segmentation
   • Receives 3D range data from a LiDAR sensor as input and segments the data into individual objects.
2. Bounding box projection
   • Receives 3D position information.
   • Projects each bounding box onto a corresponding 2D camera input image with the distance information.
3. Time to collision calculation
   • Computes the ToC for each object based on its distance from the vehicle and vehicle's velocity measured by IMU.
   • Location and size of a RoI(rectangle) are determined so that all objects within a constant ToC threshold($2s$) are included.

Network Split Module

Network split module decomposes a DNN task into two sub-tasks by creating two threads.
The inference threads share all their network model parameters.

Race condition: Both threads access the network parameters in a mutually exclusive manner as they are executed sequentially.

Overwrite the result of mandatory task: DNN-SAM provides a dedicated memory space for each thread to store its inference result.

For Transparency

• Fully-convolutional networks naturally operate on an input of any size.
• Also produce an output of the corresponding spatial dimensions.
• There are some techniques to efficiently convert a non-FCN network to an equivalent FCN network.

Network Merge Module

First, each object detected by sub-tasks should be projected on to the original input space.

Then the merge module performs deduplication through IoU.

For cut-off objects, instead of dividing by area of union, the proposed metric divides area
of intersection by area of cut-off object’s bounding box.

If the score between two bounding boxes, one of the boxes is eliminated.

Sub-task Scheduler

Sub-task scheduler runs ad a background daemon via a Named Pipe IPC which facilitates an efficient communication between sub-tasks and the scheduler.

• Maintains each DNN task’s S&M DNN execution model parameters.
• Maintains a priority queue for scheduling mandatory and optional sub-tasks according to their priorities.
• After recieving a ready message from the sub-task, enqueues the subtask into the priority queue with PID and deadline information.
• After recieving a complete message, dequeues sub-task from the queue according to the scheduling algorithm.
• Also continuosly calculates available slack at each invocation and determines the scales of optional sub-tasks.

Scheduling of Multiple DNN Tasks for Object Detection

We want to maximize the overall detection accuracy while meeting all timing constraints.

1. How to model each DNN task associated with the proposed S&M DNN execution?
2. How to schedule sub-tasks of multiple DNN tasks?
3. How to provide offline timing guarantees for the scheduling?

Split-and-Merge DNN Execution Model

Each task $\tau_i \in \tau$ can be specified as $\tau_i = (\tau^M_i, \tau^O_i, T_i, D_i)$. The executions are non-preemtive in a sub-task level.

• A mandatory sub-task $\tau^M_i$ is specified as $\tau^M_i = (R^M_i, C^M_i)$
  • $R^M_i = \{(x,y), (w,h)\}$: center position $(x, y)$ and the maximum size $(w, h)$ of RoI
  • $C^M_i$: WCET of $\tau^M_i$
    $C^M_i = c^\textrm{RoI}_i + c^\textrm{Split}_i + c^\textrm{Infer}_i \tag{1}$
  • Maximum size of RoI and WCET are assumed known a priori.
• An optional sub-task $\tau^O_i$ is specified as $\tau^O_i = (S^O_i, C^O_i)$
  • $S^O_i$: a finite set of scales. (eg. $S^O_i = \{0, 160, 256, 320, 416, 512, 608, 672\}$)
  • $C^O_i = \{C^O_i(s_i) | s_i \in S^O_i\}$: a set of WCET at different scales.
    $C^O_i(s_i) = c^\textrm{Infer}_i(s_i) + c^\textrm{Merge}_i \tag{2}$

Scheduling of Multiple DNN tasks

The following objectives must be achieved:

1. Scheduling mandatory sub-tasks as early as possible to detect objects in RoI as quickly as possible.
2. Scheduling optional sub-tasks with a large scale to maximize the overall accuracy, while meeting the deadlines of all the jobs of mandatory and optional sub-tasks.

Suppose every mandatory sub-task $\tau^M_i$ is always assigned its resource based on the maximum size of RoI and its corresponding worst-case execution time $C^M_i$.

We can utilize unused resources for optional sub-tasks and improve the overall accuracy.

We propose two different scheduling policies. i) EDF-MandFirst, ii) EDF-Slack.

• Different prioritization schemes
• Different mechanisms of determining the scales of optional sub-tasks.

Determining the priority ordering

EDF-MandFirst

• EDF-MandFirst assigns statically higher priorities to mandatory sub-tasks over optional ones.
• Implemented by maintaining two queues:
  • One for active mandatory sub-tasks.
  • One for active optional sub-tasks.
• Eash sub-task group ordered by EDF policy.

EDF-Slack

• EDF-Slack assigns priorities to sub-tasks by the EDF w/o separation between mandatory and optional sub-tasks.
• Optional sub-tasks are assigned higher priorities than mandatory sub-tasks with later deadlines.

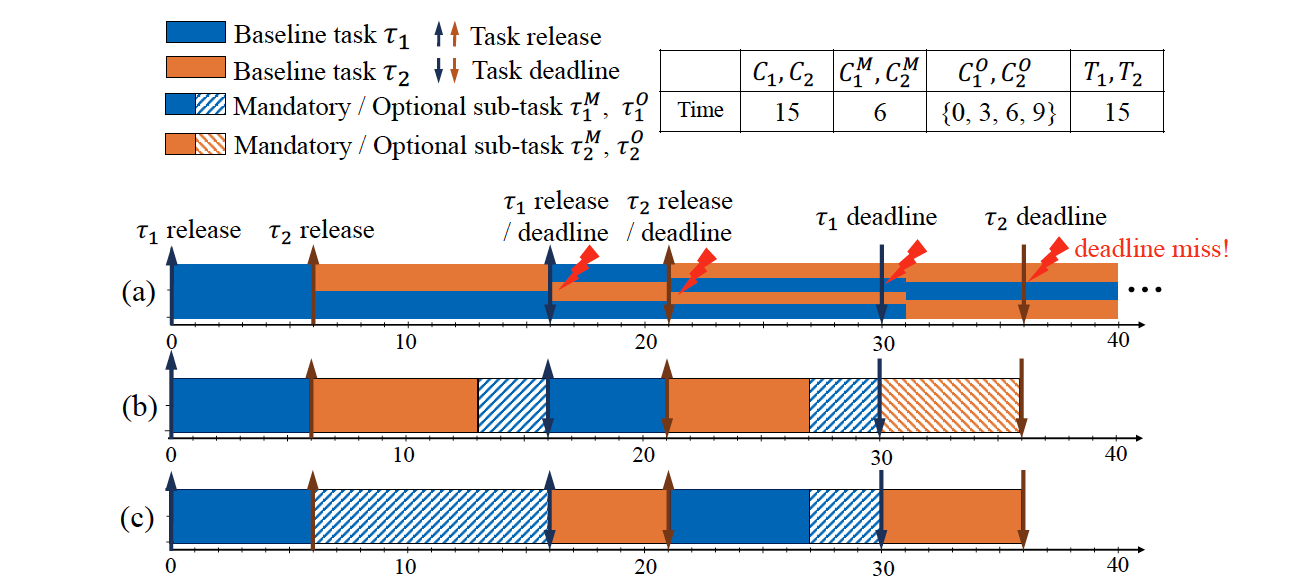
Determining the scale of optional sub-tasks for EDF-MandFirst

When an optional sub-task $\tau^O_k$ is selected to be scheduled by EDF-MandFirst at time $t_\textrm{cur}$,

• There is no active mandatory sub-task at $t_\textrm{cur}$.
• No mandatory job is released in $[t_\textrm{cur}, d_1(t_\textrm{cur}))$.

So, we can guarantee that there is no execution of any mandatory sub-task in $[t_\textrm{cur}, d_1(t_\textrm{cur}))$ and it means $\tau^O_k$ can utilize $d_1(t_\textrm{cur})-t_\textrm{cur}$ amount of slack time.: $\arg\max_{s_k \in S^O_k}\{C^O_k(s_k)|C^O_k(s_k)\le d_1(t_\textrm{cur})-t_\textrm{cur}\}$

Theorem 1
If Eq. (3) holds, $\tau$ is schedulable by EDF-MandFirst (i.e., it guarantees no sub-job deadline miss.)

$\frac{\max_{\tau^M_i \in \tau}C^M_i}{\min_{\tau^M_i \in \tau}T_i} + \sum_{\tau^M_i \in \tau}\frac{C^M_i}{T_i} \le 1.0 \tag{3}$

Proof
The following two properties holds.

1. Each optional sub-tasks does not delay any mandatory sub-task.
2. Each optional subtask does not miss its deadline.

Therefore the proof is equivalenmt to prove $\{\tau^M_i\}$ is schedulable by the vanilla non-preemptive EDF scheduling.

High-level idea for Eq. (3)
The EDF utilization bound for a set of preemptive tasks is $\displaystyle\sum_{\tau^M_i \in \tau}\frac{C^M_i}{T_i} = 1.0$
Because of the blocking of non-preemptive executions, the execution of higher-priority task is blocked by at most one currently running lower priority task.

In the worst-case scenario, a task might be blocked by the task which has the maximum execution time.

The maximum blocking factor is contributed by the task which has the shortest period.
This can explain the following term, $\displaystyle\frac{\max_{\tau^M_i \in \tau}C^M_i}{\min_{\tau^M_i \in \tau}T_i}$

Determining the scale of optional sub-tasks for EDF-Slack

We want to determine the scale of optional sub-tasks such that the execution of $\tau^O_k$ does not compromise the deadline guarantee of every mandatory sub-task.

Since we do not know the size of RoI and actual execution time of a mandatory sub-task until it's completed,

• We need to assume that the resource demand for each future mandatory sub-task is up to $C^M_k$ to guarantee no deadline miss.
• Upon completion of a mandatory sub-task, we know its actual execution time corresponding to its actual RoI size and reclaim the unused portion of assigned resources that can be counted.

Theorem 2
If Eq. (3) holds, $\tau$ is schedulable by EDF-Slack (i.e., it guarantees no sub-job deadline miss).

Proof
Due to the mechanism of determining the scale of optional sub-tasks, a lower priority optional sub-task cannot block the execution of any high-priority mandatory sub-task.
Therefore, we use the same blocking term as Eq. (3).

Then what we need to prove is EDF-Slack satisfies $𝑈^𝑀(𝑡)+𝑈^𝑂(𝑡) ≤ 1.0$ for every $𝑡$.

The algorithm updates the run-time utilization by Lines 3–5, and calculates
the largest $𝑞_𝑖$ that does not compromise $𝑈^𝑀(𝑡)+𝑈^𝑂(𝑡) ≤ 1.0$ in Line 4

This implies that the theorem holds.

Run-time complexity

EDF-MandFirst

• Calculates the slack with the complexity of $O(1)$
• Determines the scale of an optional sub-task $\tau^O_i$ from $S^O_i$ with the complexity of $O(1)$.
• Thus, $O(1)$

EDF-Slack

• Calculates the slack with the complexity of $O(n)$
• Determines the scale of an optional sub-task $\tau^O_i$ from $S^O_i$ with the complexity of $O(1)$.
• Thus, $O(n)$

Evaluation

Experimental Setup

• DarkNet
• NVIDIA Jetson Xavier(non-preemptive), Ubuntu 18.04.4, CUDA 10.0
• YOLOv3 (fully convolutional network)
• KITTI in-vehicle camera dataset.
• Velodyne LiDAR point clouds data (available on the KITTI dataset).
• Assume a constant vehicle speed. (no corresponding IMU data)
• Also implemented system for emergency braking on a 1/10 scale self-driving car.

DNN execution time profiling and run-time overhead

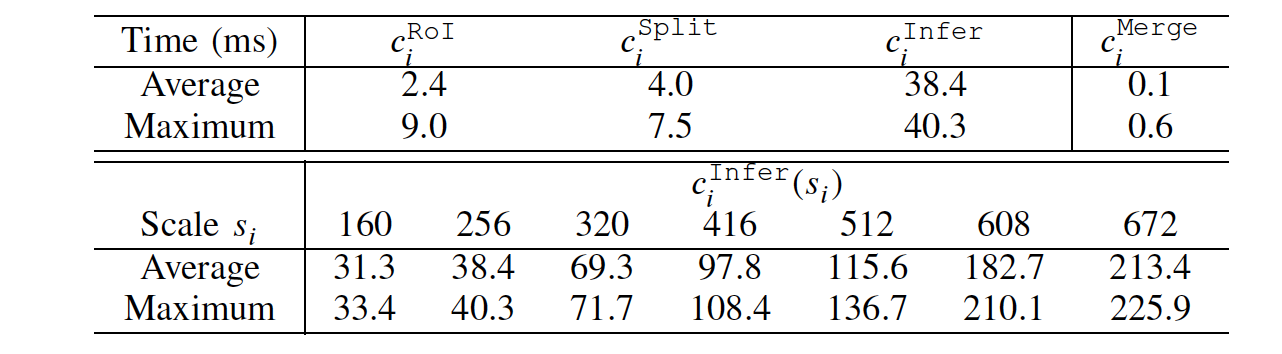
• The additional memory required by DNN-SAM is about 2,361KB per task (0.1% of the total memory usage).
• At most four YOLOv3 networks can be loaded on the Xavier due to the memory constraint.
• Scheduling overhead increases from 26.4$\mu s$ to 88.7 $\mu s$ while $n$ is increased from 1 to 100.

Comparison Setup

• The accuracy of RoI: the ratio of detected objects inside an RoI to the total ground truths

• The overall accuracy: the ratio of all detected objects to the total ground truths.

• FPS: as the inference latency metric.

• Baseline represents the SOTA DNN inference frame-work and are scheduled in a FIFO manner.

• Baseline uses the network size of 608 $\times$ 608.

• DNN-SAM uses the maximum RoI size of $w=h=256$ and network scales $S^O_i = \{0, 160, 256, 320, 416, 512, 608, 672\}$

Evaluation Result

Inference latency

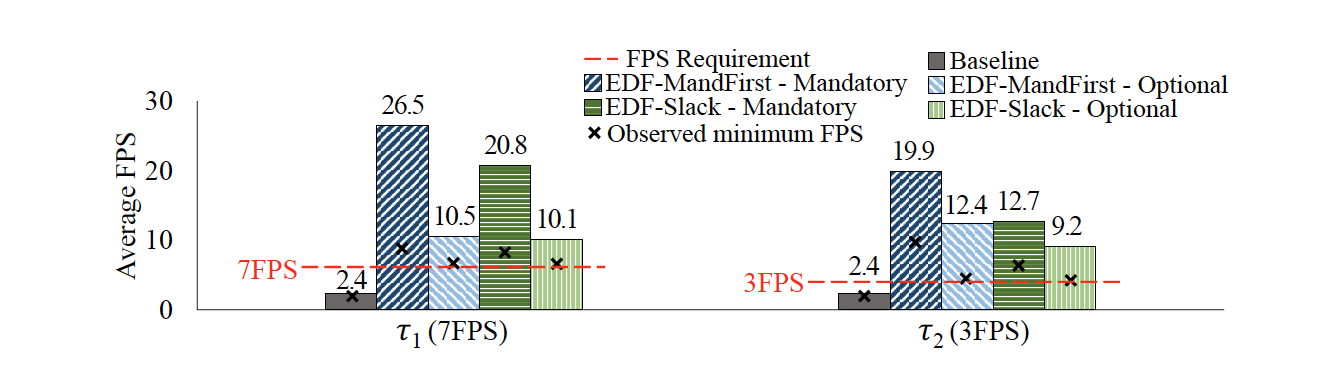
Accuracy of RoI and Overall accuracy

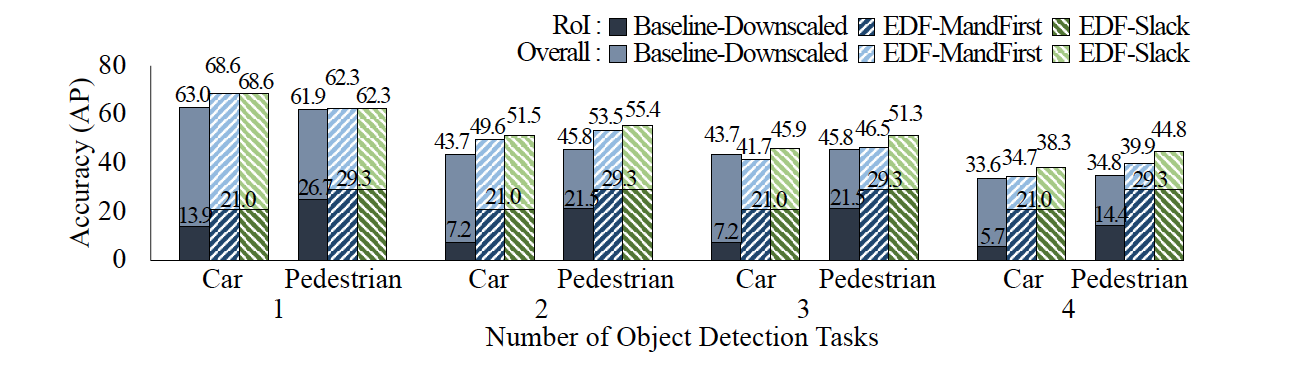
Evaluation with an increasing number of tasks

Inference latency

Accuracy of RoI and Overall accuracy

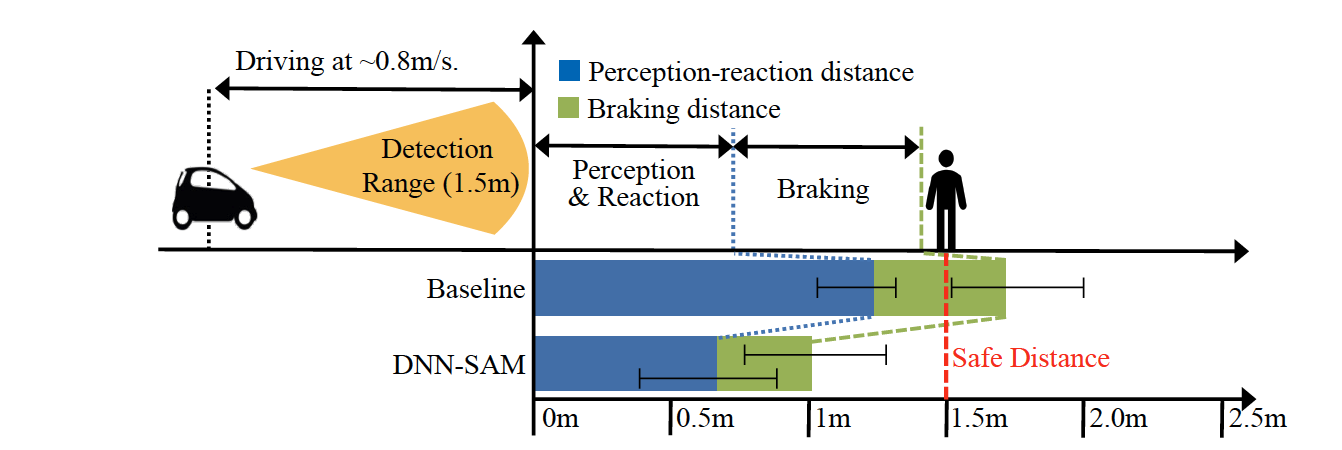
Case Study: Emergency Braking

DNN-SAM has been deployed into a 1/10 scale
self-driving car equipped with an NVIDIA Jetson Xavier to perform a case study of emergency braking.

• Executed two object detection tasks for front/back cameras both at 5 FPS.
• car is moving toward the pedestrian at 0.8m/s
• the camera's FOV is limited to 1.5m