B. Exploitation과 Exploration

learning agent에게 아래 둘은 상충하는 관계이다.

• Exploitation: 현재 지식을 기반으로 퍼포먼스를 최대화하는 것
• Exploration: 지식을 늘리는 것

우리는 최적의 결정을 내리기 위해 정보를 얻어야 하며, 그러기 위해서는 단기적인 이익을 포기해야 할 수 있다.

The Multi-Armed Bandit

Multi-Armed Bandit(여러 레버를 가진 슬롯 머신)은 다음 분포의 집합이다. $\{\mathcal{R}_a|a\in\mathcal{A}\}$

• $\mathcal{A}$는 가능한 액션의 집합이다 (레버들)
• $\mathcal{R}_a$는 $a$에 대한 보상의 분포이다.
• $t$ 스텝에, 에이전트는 $A_t\in\mathcal{A}$를 고르게 된다. (레버들 중 하나)
• 그러면 환경은 $R_t\sim\mathcal{R}_{a_t}$ 를 생성하게 된다.
• 이 게임의 목표는 누적 보상합인 $\sum^t_{i=1}R_i$를 최대화하는 것이다.
• 우리는 $\mathcal{A}$에 대한 분포인 policy를 학습해야 한다.

$a$에 대한 action value는 보상의 기댓값으로, 아래와 같이 나타난다.

이때 optimal value는 다음과 같다.

action $a$에 대한 regret은 다음과 같다.

regret이 커질수록 잘못하고 있다는 것이며, regret이 0에 가까울 수록 잘하고 있다는 것이다.

그러면 우리는 total regret을 최소화해야 한다.

보상의 누적합을 최대화하는 것은 total regret을 최소화하는 것과 동일하다.

Algorithms

우리는 다음 알고리즘들을 다뤄볼 것이다.

• Greedy
• $\epsilon$-greedy
• Policy Gradients
• UCB
• Thompson sampling

처음 세 개는 모두 다음 action value 추정을 사용할 것이다.

여기서 $Q_t$는 지금까지 $a$를 골랐을 때 보상의 평균이라고 보면 된다.

$\mathcal{I}$는 indicator function으로 $\mathcal{I}(True)=1$이며, $\mathcal{I}(False)=0$이다.

당연하게도 action $a$에 대한 count는 다음과 같다.

$Q_t(a)$를 $t$마다 업데이트하는 과정은 너무 간단하므로, 생략한다.

Greedy Algorithm

Greedy policy는 가장 높은 value를 갖는 action을 고르는 방법이다.

이는 이와 동치이다.

이 경우 suboptimal한 액션에 영원히 갇힐 수 있다는 단점이 있다.
이 때 regret은 계속 linear하게 증가하게 될 것이다.

따라서 등장하게 된것이 $\epsilon$-Greedy algirithm이다.

ϵ-Greedy algirithm

$\epsilon$-Greedy algirithm는 다음과 같다.

• $1-\epsilon$의 확률로 greedy하게 액션을 선택한다. $a = \argmax\limits_a Q_t(a)$
• $\epsilon$의 확률로 랜덤한 액션을 선택한다.

이는 아래와 동치이다.

이 알고리즘은 greedy와 다르게 exploration을 계속할 수 있다는 것을 알 수 있다.

Policy gradients

값을 학습하는 것 대신에 $\pi(a)$를 직접 학습할 수 있을까?

예를 들어 action preferences를 $H_t(a)$라고 하고, 와 policy를

라고 정의하자. (softmax)

여기서 preferences는 value와 다르다. 그냥 학습가능한 policy의 매개변수이다.

우리는 policy 매개변수를 value의 기댓값이 증가하도록 업데이트해야하며,
이때 gradient ascent를 사용할 수 있다.

여기서 $\theta$는 현재 policy 매개변수이다.

하지만 $\nabla_\theta\Bbb{E}[R_t|\pi_{\theta_t}]$를 바로 계산하기는 어렵다.
따라서 log-likelihood trick (또는 REINFORCE trick)을 사용하여 식을 변형해줄것이다.

정리하자면 아래와 같다.

따라서 위의 gradient ascent에 이를 sample을 통해 적용하면 아래와 같아진다.

이를 policy의 value에 대한 stochastic gradient ascent라고 부른다.

이를 통해 우리는 value에 대한 추정을 하지 않아도 되고, 단지 sampled reward만 사용해도 된다.

자, 이제 이 예시를 위의 softmax에 적용해보자.

이는 아래와 같이 쓸 수 있다.

이 경우 local optimum에 빠질 수 있다. 즉 이것만으로는 exploration 문제를 해결할 수 없으나, deep reinforcement learning으로 가는 가이드라인을 잡아준다.

Policy gradients with baselines

$\sum_a \pi_\theta(a) = 1$이기 때문에 $\theta$와 $a$에 의존성이 없는 어떤 $b$에 대해서라도 아래 식이 성립한다.

이 뜻은 우리가 baseline을 정할 수 있다는 뜻이며,

원래 식을 아래와 같이 바꿔 사용할 수 있다.

Theory: what is possible

이쯤에서 우리는 해봤자 얼마나 더 잘 할 수 있을까? 우리가 희망하는 베스트는 어디까지인가를 할 필요가 있다.

이를 위해 다음 정리를 소개한다.

Lai and Robbins Theorem

$\lim\limits_{t\rarr\infin}L_t \ge \log t \sum\limits_{a|\Delta_a>0}\frac{\Delta_a}{KL(\mathcal{R}_a||\mathcal{R}_{a^*})}$

( Note: $KL(\mathcal{R}_a||\mathcal{R}_{a^*}) \propto \Delta_a^2$ )

이를 통해 우린 regret이 적어도 logarithmic하게 상승한다는 것을 알 수 있다.

즉, 우리가 얼마나 좋은 알고리즘을 생각하던간에 regret은 최소 logarithmic하게 증가한다는 것이다.

일단 지금까지 봐온 $\epsilon$-greedy나 policy gradient는 regret이 linear하게 증가한다. 그럼 logarithmic한 upper-bound를 가지는 알고리즘이 존재할까?

당연히 있다!

Counting Regret

일단 그전에, regret을 좀 다르게 접근해보자.

위에서 action a에 대한 regret은 아래와 같이 계산했다.

그리고 total regret은 다음과 같다.

제일 오른쪽 변을 보게 되면, 결국 $\Delta_a$가 큰 액션에 대해서는 더 적은 count를 가져야 좋은 알고리즘이 된다는 것을 알 수 있다.

Optimism in the face of uncertainty

Optimism in the face of uncertainty: 불확실할때는 낙관적이게.

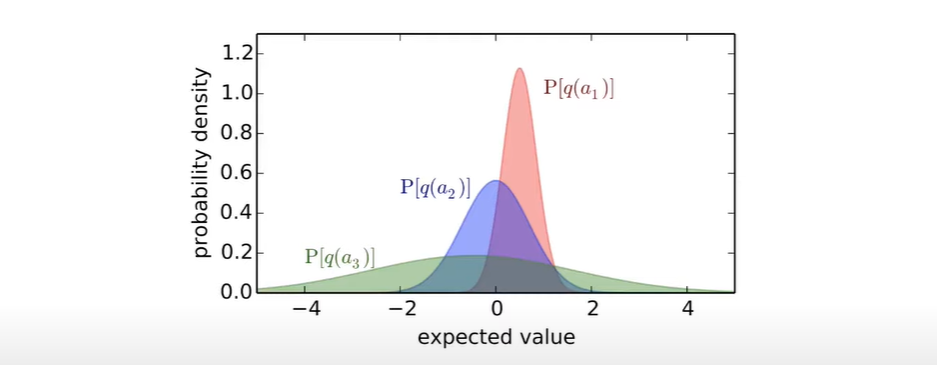
이런식으로 action들의 value 분포가 있다고 할 때, $a_3$를 골라 exploration을 수행하라는 말이다. 이를 구체적으로 정책화한 것이 UCB이다.

Upper Confidence Bounds(UCB)

우선 각 action value들에 대해 upper confidence $U_t(a)$를 설정한다. 이는 높은 확률로 아래 식을 만족해야 한다.

이때, upper confidence bound(UCB)가 가장 큰 액션을 선택한다.

여기서 불확정성은 해당 액션이 선택된 횟수인 $N_t(a)$에 의존할 것이며, $N_t(a)$가 작으면 $U_t(a)$가 클 것이고, $N_t(a)$가 크다면 $U_t(a)$가 작을것이다.

따라서 action $a$는 $Q_t(a)$가 크거다 (좋은 액션) 아니면 $U_t(a)$가 클 때 (높은 불확정성) 선택될 것이다.

Theory: the optimality of UCB

Hoeffding's Inequality (simplified ver.)

$X_1, \cdots, X_n$이 $[0,1]$의 독립항등분포를 따르고, $\mu = \Bbb{E}[X]$라고 정의하며, 표본기댓값을 $\overline{X}_t=\frac{1}{n}\sum^n_{I=1}X_i$라 하자.
이때 다음 부등식이 성립한다.

$p\left( \overline{X}_n + u \le \mu \right) \le e^{-2nu^2}$

우리는 호에프딩 부등식을 범위가 주어진 보상을 받는 슬롯머신에 대입할 수 있다.

만약 $R_t\in[0,1]$이라면

가 성립한다. 그리고 대칭적으로 아래식도 성립한다.

Calculating UCB

이를 통해 우리는 UCB를 추정할 수 있다. 만약 UCB에서 정하는 최대 확률을 $p$라고 한다면,

그럼 $p$는 어떻게 구할까?

여기서 우리는 reward를 더 많이 받을 수록 $p$를 줄여나가는 방향을 생각해볼 수 있다.
$p = 1/t$처럼 말이다.

이렇게 하면 우리는 계속 exploring을 시행할 것이지만, 너무 많이는 하지 않게 할 수 있을 것이다.

자 이제, 다시 원래 식으로 돌아와서 보다면, UCB는 다음과 같이 쓰여진다.

$a_t = \argmax\limits_{a\in\mathcal{A}}Q_t(a) + cU_t(a)\sqrt{\frac{\log t}{2_t(a)}}$

그럼 여기서 다음과 같은 직관을 얻을 수 있다.

• 만약 $\Delta_a$가 크면, $N_t(a)$가 작을 것이다. $Q_t(a)$가 작을 것이기 때문이다.
• 따라서 $\Delta_a$가 작던지, $N_t(a)$가 작을 것이며,
• 또한 우리는 $\Delta_a N_t(a) \le O(\log t)$ 가 모든 $a$에 대해 만족한다는 것을 증명할 수 있다.

Theorem (Auer et al., 2002)

$c=\sqrt{2}$인 UCB는 다음을 만족하는 total regret을 갖는다.

Bayesian Bandits

우리는 $p(q(a) | \theta)$에 대해 Bayesian Approach를 적용해볼 수도 있다.

예를 들어 $\theta_t$는 평균과 분산을 포함할 수 있다.

이렇게 이는 prior information인 $\theta_t$를 주입할 수 있게 해준다.

Example

reward가 베르누이 분포 (0또는 1)를 갖는다고 가정해보자.

이때 각 액션마다, 사전분포는 $[0, 1]$에서의 균일 분포가 될 수 있다.

그리고, 사후분포는 $x_a = 1$, $y_a = 1$인 베타분포 $\beta(x_a, y_a)$가 될 것이다.

이때 사후분포 업데이트는 다음과 같이 이뤄질 깃이다.

• $R_t = 0$인 경우 $x_{A_t} \larr x_{A_t} + 1$
• $R_t = 1$인 경우 $y_{A_t} \larr y_{A_t} + 1$

$R_1 = +1$, $R_2 = +1$, $R_3 = 0$, $R_4 = 0$이라고 가정하면 사후분포는 아래 그림과 같이 바뀔 것이다.

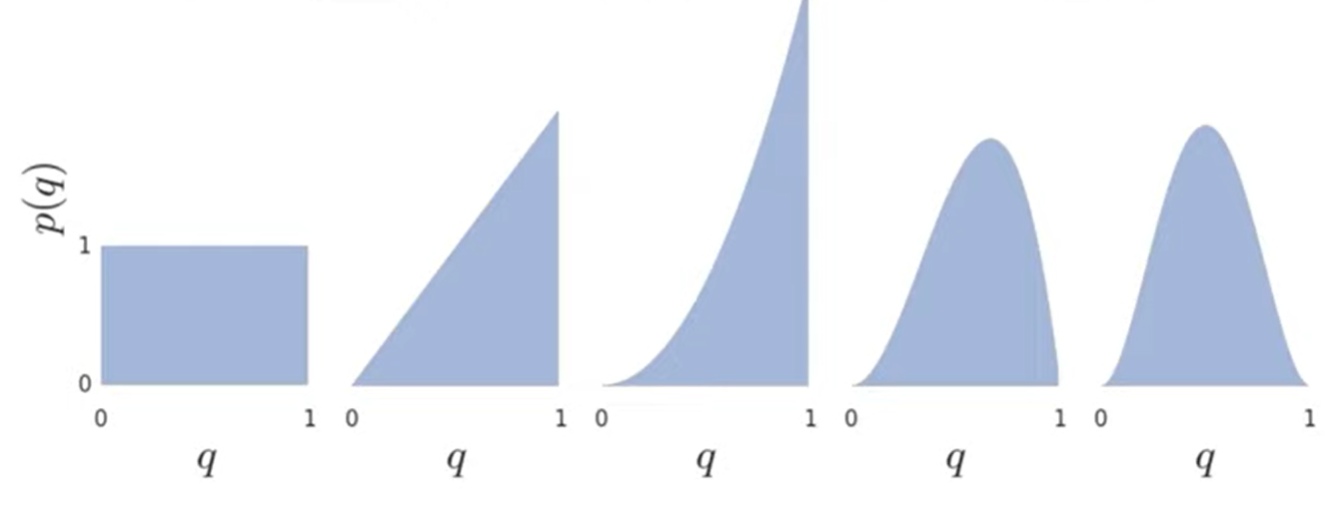
Bayesian Bandits with Upper Confidence Bounds

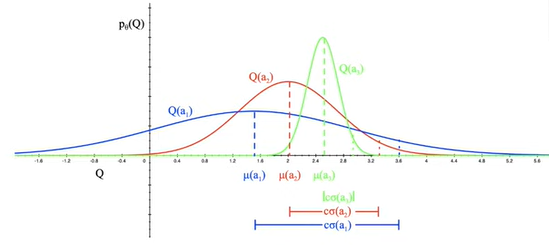
이를 이용하여 사후분포를 통해 upper confidence를 추정할 수 있을 것이다.

예를 들면 $U_t(a) = c\sigma_t(a)$처럼 할 수 있을 것이고, $Q_t(a) + c\sigma_t(a)$를 최대화하는 액션을 고르면 될 것이다.

Thompson sampling

Probability Matching

UCB에 활용하는 것 말고도, 확률적 매칭을 사용하는 방법이 있다.

이는 $a$가 optimal할 확률에 따라 $a$ 액션을 고르는 방법이다.

이는 불확실할때는 낙천적이게 방법이다. 액션들은 추정값이 높거나, 불확실성이 높을 때 높은 확률을 갖게 될 것이다.

이때 $\pi(a)$를 사후분포로부터 계산하는 것이 어려울 수도 있다.

Thompson Sampling

톰슨 샘플링은, $Q_t(a) \sim p_t(q(a)), \forall a$로 샘플링을 한 후 그 중 가장 큰 값을 선택하는 방법이다.

간단히 말해 분포와 x축 사이의 면적 전체에서 임의의 점을 하나 뽑은 후, 그 점들의 x값 비교를 통해 고른다고 볼 수 있다.

$A_t = \argmax\limits_{a \in \mathcal{A}}Q_t(a)$

따라서 톰슨 샘플링은 샘플 기반 확률적 매칭이라고 볼 수 있다.

Bernoulli bandits에 대해서 톰슨 샘플링은 regret이 Lai and Robbins lower bound를 만족하므로 optimal하다.

Example

액션 $a$, $b$에 대해 0과 1만을 reward로 내보내는 bandit에서 다음과 같은 상황을 가정하자.

• 첫 번째 시행에서 $a$를 고름. => $R_1 = 0$
• 두 번째 시행에서 $b$를 고름. => $R_2 = 1$

이때 각 알고리즘들에 대해 세 번째 단계에 액션 $a$를 선택할 확률, 즉 $P(A_3=a)$를 구해보자.

1. Greedy Algorithm
   현 상황에서는 당연히 b를 고를 수밖에 없다. 아마 앞으로도 무한히 b만 고를 것이다.
   따라서 $P(A_3=a) = 0$

2. $\epsilon$ - greedy
   $\epsilon$ - greedy의 $\pi$ 함수를 다시 가져와 보자.

   $\pi_t(a) = \begin{cases} (1-\epsilon) + \epsilon/|\mathcal{A}| &\text{if } Q_t(a) = \max_b Q_t(b)\\ \epsilon/|\mathcal{A}| &\text{otherwise} \end{cases}$

   따라서 $|\mathcal{A}|$가 2이므로, $P(A_3=a) = \epsilon/2$ 가 된다.

3. UCB
   UCB는 결정론적 알고리즘으로, 현 상횡에서 $b$를 고를 수밖에 없다.
   (불확실성은 똑같고, value의 기댓값은 b가 더 높음)
   $P(A_3=a) = 0$

4. Thompson sampling
   $a$의 사후확률분포는 $\beta(1,2)$ 이며 $b$의 사후확률분포는 $\beta(2,1)$이 된다. 따라서, 이때 $a$가 선택될 확률을 구해보자.

   Thx to Sangwon Lee

   $a$가 임의의 $x$좌표 $t$에 있을 확률은 $(2-2t)dt$일 것이다. 그때 $b$가 $t$보다 작을 확률은 $\int^t_0 2xdx = t^2$이 되므로, $b$가 $a$보다 작을 확률은 $t^2(2-2t)dt$로 나타난다.

   $t \in [0,1]$이므로 이를 정적분하면 $\int^1_0 t^2(2-2t)dt = \frac{1}{6}$이 될 것이다.