C. 마르코프 결정 과정과 DP

Formalising the RL interaction

우선 환경이 fully observable하다고 가정하자.

참고로 거의 모든 RL 문제들은 MDP로 형식화할 수 있다.

• Partially observable problem 도 MDP로 변환할 수 있다.
• Bandit은 한개의 상태를 가지는 MDP이다.

Markov Decision Process
Markov Decision Process는 $(\mathcal{S}, \mathcal{A}, p, \gamma)$이다.

• $\mathcal{S}$는 모든 가능한 상태들의 집합이다.
• $\mathcal{A}$는 모든 가능한 액션들의 집합이다.
• $p(r,s' | s,a)$는 현재 상태가 $s$이고, 액션 $a$를 수행했을 때, 리워드가 $r$이고, 다음 상태가 $s'$일 결합확률이다.
• $\gamma \in [0,1]$는 discount factor로, 나중의 보상과 일찍의 보상의 가중치를 분배한다.

여기서 우리는 다음의 관찰을 할 수 있다.

• $p$는 문제의 dynamics를 정의한다.
• 가끔은 상태의 변화나 reward의 기댓값을 제외하는 것이 유용할 때도 있다.
  $p(s'|s,a) = \sum\limits_r p(s',r|s,a)\qquad\qquad\Bbb{E}[R | s, a] = \sum\limits_r r \sum\limits_{s'} p(r, s'| s,a)$

이는 MDP의 다른 정의를 만들 수 있다. 둘은 완전히 동치이다.

Markov Decision Process (Alternative Definition)

Markov Decision Process는 $(\mathcal{S}, \mathcal{A}, p, r, \gamma)$이다.

• $\mathcal{S}$는 모든 가능한 상태들의 집합이다.
• $\mathcal{A}$는 모든 가능한 액션들의 집합이다.
• $p(s' | s,a)$는 현재 상태가 $s$이고, 액션 $a$를 수행했을 때, 다음 상태가 $s'$일 확률이다.
• $r:\mathcal{S}\times\mathcal{A} \rarr \Bbb{R}$은 보상의 기댓값으로, $(s,a)$에 의해 얻어진다.

$r = \Bbb{E}[R | s, a]$

• $\gamma \in [0,1]$는 discount factor로, 나중의 보상과 일찍의 보상의 가중치를 분배한다.

또 하나의 정의를 알아보자.

Markov Property
시간으로 인덱스된 랜덤한 변수들의 수열 $\{S_t\}_{t \in \Bbb{N}}$을 생각해보자.
이때 $\forall s' \in \mathcal{S}$에 대해 다음 조건을 만족하면 state $s$가 Markov Property를 가진다고 말한다.

$p(S_{t+1} = s' | S_t = s) = p(S_{t+1} = s' | h_{t-1}, S_t = s)$

(단, $h_{t-1} = \{S_1, \cdots, S_{t-1}, A_1, \cdots, A_{t-1}, R_1, \cdots, R_{t-1}\}$)

MDP에서 모든 상태는 Markov Property를 가진다고 가정한다.

• state는 history로부터 모든 연관된 정보를 갖고 있다.
• state를 알고 있다면, history는 버려도 된다.
• state는 충분한 과거의 정보이다.

Formalising the objective

Returns

MDP에서 수행한 액션이 즉시 리워드 $R_t$$로 이어진다면 return을 다음과 같이 계산할 수 있다.

• Undiscounted return (episodic / finite horizon pb.)

  $G_t = R_{t+1} + R_{t+2} + \cdots + R_T = \displaystyle\sum^{T-t-1}_{k=0}R_{t+k+1}$

• Discounted return (finite or infinite horizon pb.}

  $G_t = R_{t+1} + \gamma R_{t+2} + \cdots + \gamma^{T-t} R_T = \displaystyle\sum^{T-t-1}_{k=0}\gamma^k R_{t+k+1}$

• Average return (continuing, infinite horizon pb.)

  $G_t = \frac 1 {T-t-1} (R_{t+1} + R_{t+2} + \cdots + R_T) = \frac 1 {T-t-1}\displaystyle\sum^{T-t-1}_{k=0}R_{t+k+1}$

Discounted Return

infinite horizon $T \rarr \infin$에 대한 Discounted Return $G_t$는 다음과 같다.

여기서 discount $\gamma \in [0,1]$은 미래의 reward가 현재에 가지는 가치라고 볼 수 있다.

• $k+1$ 번의 스텝 이후에 받을 리워드 $R$의 가치는 $\gamma^k R$이다.
• $\gamma < 1$에 대하여 당장의 보상이 나중의 보상보다 더 중요하다.
• $\gamma$가 0에 가까울수록 근시안적이며,
• $\gamma$가 1에 가까울수록 원시안적이라고 볼 수 있다.

Why discount?

거의 대부분의 Markov decision process들은 discount를 사용한다. 왜일까?

• 문제 구체화:
  • 당장의 보상이 실제로 좀더 중요할 것이다.
  • 인간/동물의 행동이 실제로 당장의 보상을 선호하는 것으로 보인다.
• 문제 해결적 측면:
  • 수학적으로 보상을 깎는 것이 편리하다.
  • cyclic Markov process에서 무한한 return을 가지는 걸 피할 수 있다.

Policies

RL agent의 목표
return $G_t$의 값을 최대화하는 policy를 찾는 것.

Policy는 $\pi : \mathcal{S} \times \mathcal{A} \rarr [0,1]$의 매핑이며, 임의의 상태 $s$에 대한 임의의 액션 $a$에 대하여 상태 $s$일 때 액션 $a$를 선택할 확률을 제시한다. 이는 $\pi(a|s)$로 표기한다.

결정론적 policy에 대해 우리는 때때로 $a_t = \pi(s_t)$와 같은 표기를 사용하기도 한다.

Value Functions

• value function $v(s)$는 상태 $s$에 대한 장기간적 가치를 나타낸다.

• 우리는 action value 또한 정의할 수 있다.

• 이 둘 사이 관계를 다음과 같이 나타낼 수 있다.

Optimal Value Function

Optimal state-value function $v^*(s)$는 모든 정책중 최대값을 갖는 value function이다.

optimal action-value function $q^*(s,a)$는 모든 정책중 최대값을 갖는 action-value function이다.

optimal value function은 MDP에서 가능한 최고의 성능을 가지며, 이 optimal value function을 알게 되었을 때, 우리는 MDP가 "해결되었다"고 할 수 있다.

Optimal Policy

이 $q^*(s,a)$를 찾아냄으로써 우리는 optimal한 policy를 찾을 수 있다.

이때 policy간의 부분순서를 다음과 같이 정의한다면,

다음과 같은 정리를 얻을 수 있다.

Theorem (Optimal Policies)
모든 Markov decision process에 대해

• 다음을 만족하는 optimal policy $\pi^*$가 존재 한다.
  $\pi \ge \pi' \forall \pi$
• 모든 optimal policy들은 optimal value function을 만족한다.
  $v^{\pi^*}(s) = v^*(s)$
• 모든 optimal policy들은 optimal action-value function을 만족한다.
  $q^{\pi^*}(s,a) = q^*(s,a)$

여기서 우리는 다음과 같은 관찰을 할 수 있다.

• 모든 MDP는 결정론적 optimal policy가 존재한다.
• 만약 우리가 $q^*(s,a)$를 알게 된다면, 우리는 즉시 optimal policy또한 알게 된다.
• 여러개의 optimal policy가 있을 수도 있다.
• 만약 $q^*(s,\cdot)$을 최대화할 수 있는 여러개의 action들이 있다면, 우리는 이중 하나를 고르면 된다. (물론 확률론적 선택도 가능하다)

Bellman Equations

Value Function

Value function을 다시 가져와보자.

• value function $v(s)$는 상태 $s$에 대한 장기간적 가치를 나타낸다.

• 이는 재귀적으로 정의할 수도 있다. (마지막 줄은 기댓값을 명시적으로 작성한 것이다)

Action values

Action value 또한 재귀적으로 나타낼 수 있다.

Bellman Equations

따라서 우리는 다음 정리들을 얻을 수 있다.

Theorem (Bellman Expectation Equations)
MDP, $\mathcal{M}=\lang\mathcal{S},\mathcal{A},p,r,\gamma\rang$ 가 주어졌을 때, 모든 policy $\pi$에 대하여 value functions들은 다음 기댓값 방정식을 만족한다.

$v_\pi(s) = \sum\limits_a \pi(a|s) \left[r(s,a)+ \gamma\sum\limits_{s'}p(s'| a,s) v_\pi(s')\right]$

$q_\pi(s,a) = r(s,a)+ \gamma\sum\limits_{s'}p(s'| a,s)\sum\limits_{a' \in \mathcal{A}}\pi(a'|s') q_\pi(s',a')$

Theorem (Bellman Optimality Equations)
MDP, $\mathcal{M}=\lang\mathcal{S},\mathcal{A},p,r,\gamma\rang$ 가 주어졌을 때, 모든 policy $\pi$에 대하여 value functions들은 다음 기댓값 방정식을 만족한다. $v^*(s) = \max\limits_\pi v_\pi(s)$

$v^*(s) = \max\limits_a \left[r(s,a)+ \gamma\sum\limits_{s'}p(s'| a,s) v^*(s')\right]$

$q^*(s,a) = r(s,a)+ \gamma\sum\limits_{s'}p(s'| a,s)\max\limits_{a' \in \mathcal{A}} q^*(s',a')$

Solving RL problems using the Bellman Equations

RL Problem이란?

1. $v_\pi$ 또는 $q_\pi$를 계산하기. (policy evaluation 또는 prediction이라고 부름)
   • 정책이 주어졌을 때, 그 행동에 대해 return의 기댓값은 얼마일까?
   • 트레이딩 전략 또는 치료 프로토콜이 주어졌을 때 return의 기댓값은 얼마일까?
2. $v_*$ 또는 $q_*$를 계산하기. (control이라고 부름.)

• 가장 최적의 행동은 무엇일까 가장 최적의 value function은 무엇일까?
• 가장 최적의 치료법은 무엇일까? 시간과 연료 소모를 최소화하는 최적의 정책은 무엇일까?

Example

다음과 같은 MDP를 가정하자.

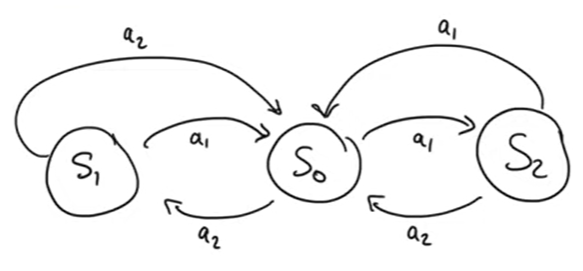
• 각 action들은 0.9의 성공확률과 0.1의 실패확률을 갖는다. 실패 시 원래 상태에 남는다.
• $S_0$으로 향하는 모든 transition은 $R_t=0$이며 나머지는 $R_t=-1$이다.

Question: Evaluation problems ($\gamma = 0.9$)

• $\pi(s) = a_1(\rarr), \forall s$에 대한 $v_\pi$는?
• 균일하게 랜덤한 정책에 대한 $v_\pi$는?
• 같은 문제를 $\gamma = 0.0$에 대해 계산한다면?

Bellman Equation in Matrix Form

$\pi$가 주어졌을 때, Bellman value equation은 다음과 같이 행렬의 형태로 나타낼 수 있다.

여기서 각 행렬의 원소는 다음과 같다.

• $\textsf{\textbf{v}}_i = v(s_i)$
• $\textsf{\textbf{r}}^\pi_i = \Bbb{E}[R_{t+1} | S_t = s_i, A_t \sim \pi(S_t)]$
• $\textsf{\textbf{P}}^\pi_{ij} = p(s_j | s_i) = \sum\limits_a \pi(a | s_i)p(s_j | s_i, a)$

이 선형 방정식을 풀면 다음과 같은 식을 얻을 수 있다.

이때 시간복잡도는 $\textsf{O}(|\mathcal{S}| ^3)$이며, 이는 작은 문제에서나 가능한 일이다.

문제가 커진다면 아래와 같은 iterative method들을 사용할 수 있다.

• Dynamic programming
• Monte-Carlo evaluation
• Temporal-Difference learning

Solving the Bellman Optimality Equation

Bellman Optimality Equation은 선형이 아니다.
따라서 일반적으로 같은 행렬적 방법을 사용할 수 없다.

따라서 다음과 같이 많은 iterative method들이 있다.

• 모델을 사용하는 방법
  • Value iteration
  • Policy iteration
• 샘플을 이용하는 방법
  • Monte Carlo
  • Q-learning
  • SARSA

Dynamic Programming

Dynamic programming은 환경의 완벽한 모델이 MDP로서 주어졌을 때, 최적의 정책을 계산하는데 사용할 수 있는 알고리즘들이다.

우리는 MDP를 해결하기 위한 몇가지 dynamic programming 방법들을 알아볼 것이며, 각 방법들을 크게 두 부분으로 나누어서 볼 것이다.

• policy evaluation
• policy improvement

Policy evaluation

우선 어떻게 이 식을 계산할것인지에 대해 생각해보자.

아이디어: 이 방정식을 업데이트로 생각하자.

Algorithm

• 먼저 $v_0$를 초기화한다. (예를 들면 0으로)
• 그 다음 다음 식을 반복한다.
  $\forall s: v_{k+1}(s) \larr \Bbb{E}[R_{t+1} + \gamma v_k(S_{t+1}) | s, \pi]$
• 만약 $\forall s: v_{k+1}(s) = v_k(s)$가 되었다면 우리는 $v_\pi$를 찾을 수 있다.

혹자는 이 알고리즘이 언제나 수렴할 수 있는지 물어보겠지만, 이 알고리즘은 적절한 조건 하에 항상 수렴한다. 이에 대한 이야기는 나중에 다룬다.

Policy Improvement

위의 방법을 사용한다면 우리는 Policy evaluation을 통해 얻은 값을 통하여 policy를 improve하는데 사용할 수 있다는 것을 알 수 있다.

만약 해당 액션을 수행하였을 때 value가 가장 커질 수 있다면 그렇게 policy를 그리디하게 선택할 수 있다는 것이다. (이는 일반적으로 참은 아니다.)

Algorithm
다음 연산을 이용하여 반복한다.

$\forall s: \pi_{new}(s) = \argmax\limits_a q_\pi (s,a)\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\\\quad\quad\quad\quad\;\;\; = \argmax\limits_a \Bbb{E}[R_{t+1} + \gamma v_\pi (S_{t+1}) | S_t = s, A_t = a]$

이렇게 $\pi_{new}$를 계산하고 반복한다.

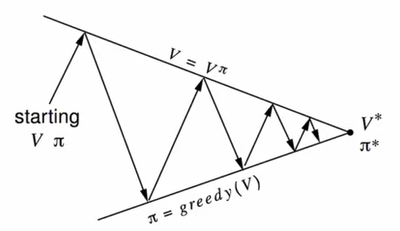
그럼 이러한 의문을 가질 수 있다.

• policy evaluation이 $v_\pi$로 수렴해야 할까?
• 아니면 그냥 가깝다면 멈춰도 될까?
  (예를 들어 value의 변화에 역치를 두는 방법으로?)
  • 아니면 간단하게 $k$번 반복한 후에 멈춰도 되지 않을까?
• 좀더 극단적으로: 그냥 첫번째 게산 이후에 policy를 업데이트하지 않는 방법은 어떨까?

Value Iteration

우리는 Bellman optimality equation을 다음과 같이 바꿀 수 있다.

이는 두 그리디한 policy improvement 스텝을 하나의 policy evaluation 안에 하는 policy iteration과 똑같다.

Algorithm: Value Iteration

• $v_0$를 초기화한다.
• 다음 식을 통해 업데이트한다.
  $\forall s: v_{k+1}(s) \larr \max\limits_a \Bbb{E}[R_{t+1} + \gamma v_k(S_{t+1}) | S_t = s, A_t = a ]$
  만약 $\forall s: v_{k+1}(s) = v_k(s)$가 되었다면 우리는 $v^*$를 찾을 수 있다.

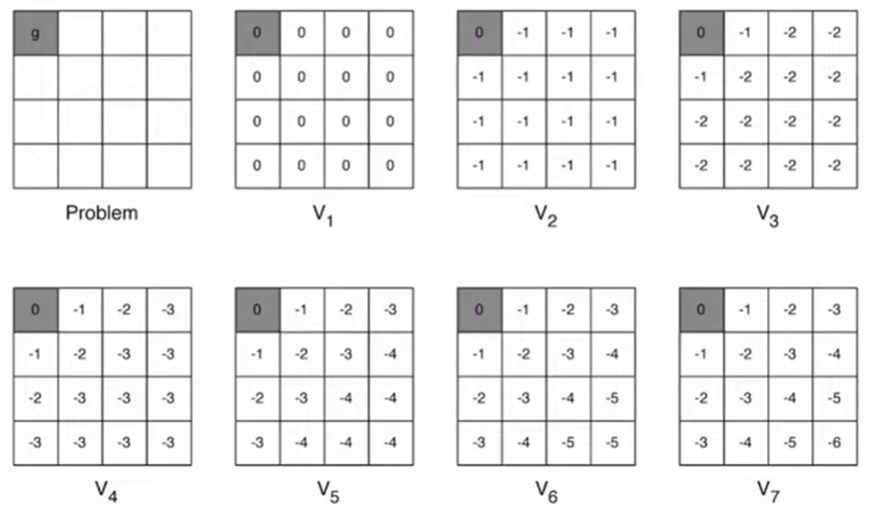
정리: Synchronous Dynamic Programming

Problem	Bellman Equation	Algorithm
Prediction	Belman Expectation Equation	Iterative Policy Evaluation
Control	Bellman Expectation Equation + (Greedy) Policy Improvement	Policy Iteration
Control	Bellman Optimality Equation	Value Iteration

• 각 알고리즘들은 state-value function $v_\pi(s)$ 나 $v^*(s)$를 각 반복 당 시간복잡도 $O(|\mathcal{A}||\mathcal{S}|^2)$를 들여 계산한다.
• 이는 action-value function $q_\pi(s,a)$ 나 $q^*(s,a)$에도 적용할 수 있으며 시간복잡도 $O(|\mathcal{A}|^2\mathcal{S}|^2)$를 갖는다.

Extensions to Dynamic programming

Asynchronous Dynamic Programming

지금까지는 synchronous한 업데이트를 사용했다. (모든 상태를 병렬적으로 업데이트하는)

이를 좀 더 개선한 방법으로 Asynchronous DP를 제안한다.

Asynchronous DP는 각 상태를 개별적으로 backup한다. 하나하나 순서대로 하는 것이 아닌 비동기적으로 하는 것이다.

여기서 back-up은 다음 state-value function을 이용하여 현재의 state-value function을 구하는 것을 말한다.

이를 통해 계산시간을 획기적으로 줄일 수 있으며, 이때 만약 모든 상태에 대하여 iteration을 한다면 이는 수렴한다는 게 보장된다.

여기에 Asynchronous DP의 세 가지 간단한 아이디어들을 소개한다.

• In-Place dynamic programming
• Prioitised sweeping
• Real-time dynamic programming

In-Place dynamic programming

동기적인 value iteration은 value function의 두 복사본을 저장한다.

In-place value iteration은 오직 하나의 복사본만을 저장한다.

Asynchronous DP가 가능하기 때문에 가능한 계산이다.

Prioitised sweeping

이는 Bellman error의 크기를 상태 선택에 사용하는 방법이다.

• 가장 Bellman error를 크게 갖는 state를 backup한다.
• 업데이트된 state의 Bellman error를 업데이트 한다.
• 이는 우선순위 큐로 쉽게 구현할 수 있다.

Real-Time Dynamic Programming

이는 agent와 관계있는 state들만 backup하는 방식이다.

예를 들어 agent가 state $S_t$에 있다면, 해당 state와 곧 도착할 것으로 예상되는 state들을 업데이트하는 방식이다.

Sample Backups

DP는 full-width 백업을 사용한다.

각 백업마다 (동기적이든 비동기적이든)

• 모든 다음 state와 action들이 고려되며
• 이는 실제 모델과 reward 함수를 사용한다.

그러나 큰 문제에서는 차원의 저주에 걸릴 수 있다.

• 상태의 개수 $n = |\mathcal{S}|$는 상태 변수의 숫자가 늘어날 수록 기하급수적으로 늘어난다.

심지어 한번의 full backup또한 너무 오래 걸린다.

따라서 다음 강좌에서는 sample backup에 대해 알아볼 것이다.

여기에서는 sample reward와 sample transition $\lang s,a,r,s'\rang$를 사용한다.

이를 통해 얻는 이익은 다음과 같다.

• Model-free: 더이상 MDP에 대한 사전지식이 필요없다.
• Sampling을 통해 차원의 저주를 풀 수 있다.
• backup의 비용이 상수이며 $n = |\mathcal{S}|$로부터 독립적이다.