FFT: Fast Fourier Transform

NPC 고급반 2주차 발표자료로 제작되었습니다.

Polynomial Multiplication

• 다항식의 곱셈은 몇몇 문제에서 활용도가 매우 높습니다.

  • 큰 수의 곱셈 ($10^n$ 정도 크기의 두 자연수 곱)
  • Goldbach's conjecture: 2보다 큰 모든 짝수는 두 소수의 합으로 나타낼 수 있다.

• 하지만 일반적으로 떠올려 볼 수 있는 알고리즘은 $O(n\cdot m)$의 Naive한 방법뿐입니다

• 오늘은 이를 $O(n\log n)$ 에 구현할 수 있는 방법을 살펴봅니다.

---

Coefficient/Point-Value Representation

Coefficient Representation

• 모든 $(n-1)$차 다항식은 상수항을 포함한 $n$개의 계수를 모두 알면 유일하게 결정할 수 있습니다. (당연히!)

• 따라서 $\{a_0, a_1, \cdots, a_{n-1}\}$ 처럼 다항식을 나타낼 수 있고, 이를 Coefficient Representation 라 부릅니다.

Point-Value Representation

• 모든 $(n-1)$차 다항식은 서로 다른 $n$개의 $\{x_0, x_1, \cdots, x_{n-1}\}$에 대한 함숫값을 알면 유일하게 결정할 수 있습니다. (Lagrangian Interpolation)

• 따라서 $\{(x_0, f(x_0)), (x_1, f(x_1)), \cdots, (x_{n-1}, f(x_{n-1}))\}$ 처럼 다항식을 나타낼 수 있고, 이를 Point-Value Representation 라 부릅니다.

---

Basic Idea for $O(n\log n)$ Polynomial Multiplication

• 두 개의 $n$차 다항식 $P(n), Q(n)$의 coefficient rep.은 이미 알고 있습니다.

• 각각을 point-value rep.으로 변환할 수 있는 $O(T)$의 알고리즘이 있다고 가정해봅시다.

• 두 point-value rep.을 알고있다면, $P(x_0)\times Q(x_0) = (P * Q)(x_0)$ 이므로, $O(n)$ 만에 $(P * Q)$의 point-value rep.을 구할 수 있습니다.

• 이를 다시 coefficient rep.으로 $O(T)$에 변환할 수 있다고 할 때, 최종적으로 $O(T+n)$에 다항식 곱셈을 수행할 수 있습니다.

• 이제 각 coefficient rep.을 point-value rep.으로 변환할 수 있는 알고리즘에 대해 다뤄봅시다!

---

Rough Sketch of Transform

• 다음 식처럼 우리는 $P(x)$를 두 $x^2$에 대한 식으로 나눌 수 있습니다.

  $\begin{aligned} P(x) &= a_0x^0 + \cdots + a_{n-1}x^{n-1} \\&= {a_0x^0 + a_2x^2 + \cdots} + x\left({a_1x^0 + a_3x^2 + \cdots}\right) \\&= A(x^2) + xB(x^2) \end{aligned}$

• 이 때,

  $A(x) = a_0x^0 + a_2x^1 + \cdots , \quad B(x) = a_1x^0 + a_3x^1 + \cdots$

  처럼 구해집니다.

• 저희는 $P(x_i)$의 값이 필요하고, 여기에 필요한 함숫값은 $A(x_i^2)$과 $B(x_i^2)$입니다. 그리고 이는 $P(-x_i)$를 구할 때도 똑같이 사용되는 걸 알 수 있습니다.

• 즉, $n$개의 $x$값을 음수-양수 pair로 잡아준다면 저희는 $n/2$개만 계산해도 됩니다!

• 따라서 크기가 $n$인 문제를 $n/2$개의 문제로 축소하는 것과 같고, $T(n) = 2T(n/2) + O(n)$이므로, 마스터 정리에 의해 $O(n\log n)$만에 문제를 풀 수 있게 됩니다.

• 그런데, 문제를 계속 쪼개는게 가능할까요?

• $2n$차 다항식에 $\{-n,-n+1,\cdots, n-1,n\} \subset \mathbb{R}$을 대입하는 문제는 결국 $n$차 다항식에 $\{1, 4, 9, \cdots, n^2\}$을 대입하는 문제로 바뀝니다.

• 이제 $\{1, 4, 9, \cdots, n^2\}$는 양수만 존재하게 되어 더 이상 문제를 쪼갤 수 없습니다.

• 실수로는 어림도 없어 보입니다. 복소수를 써야할 것 같아요.

• 1의 $2^m$제곱근을 구하면 됩니다!
  

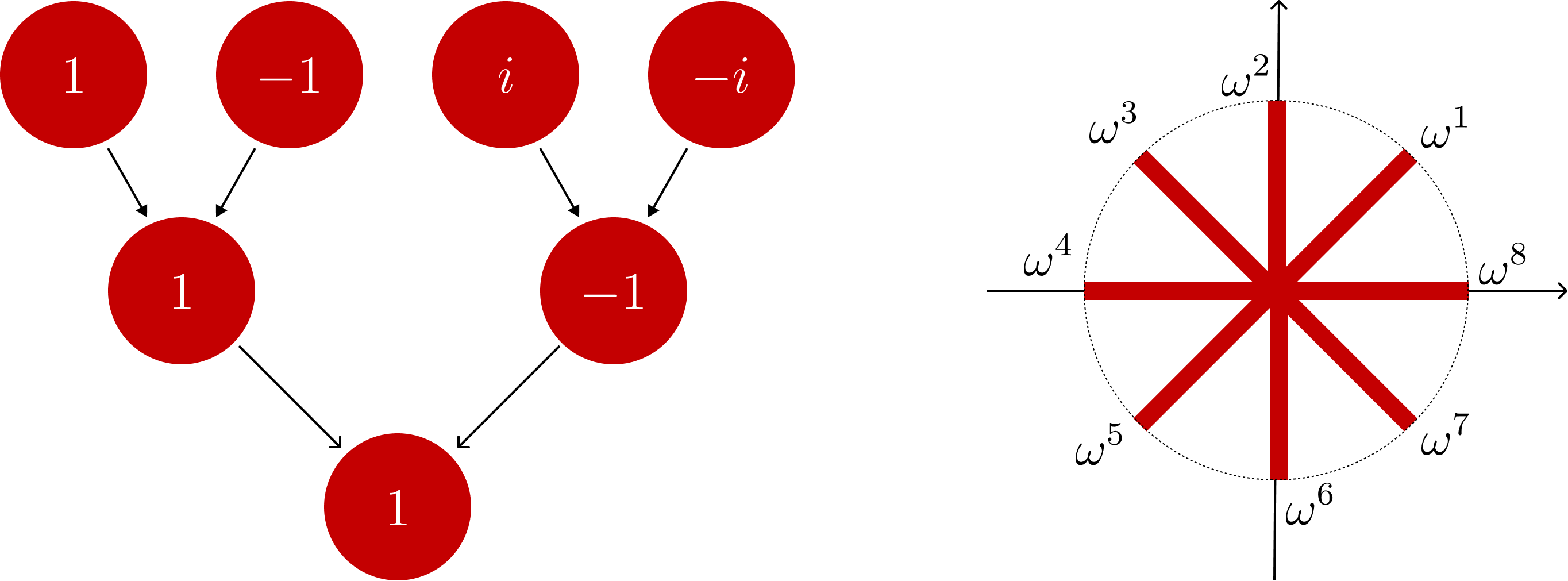
Root of unity

• 1의 $n$제곱근은 간단하게 구할 수 있습니다.

• $z^n = 1$라고 할 때, 우리는 양변의 절댓값이 같음을 이용하여 $z=\cosθ+i\sinθ$로 쓸 수 있습니다.

• 그리고 드 무아브르 공식에 의해 다음과 같이 정리됩니다.

  $\begin{aligned} 1 &= z^n \\ &= \cos nθ+i\sin nθ \end{aligned}$

• 이 식은 $n\theta = 2k\pi$일 떄 성립하고, 정리하면 저희는 다음과 같은 $n$개의 1의 $n$제곱근을 구할 수 있습니다.

  $z=\cos\frac {2kπ} n+i\sin \frac {2kπ} n,\;0 \le k < n$

DFT & IDFT

DFT: Discrete Fourier Transform

• DFT는 coefficient rep.을 point-value rep. $\{P(\omega^0), P(\omega^1), \cdots, P(\omega^{n-1})\}$로 바꾸는 변환입니다.
• 이를 수식으로 나타내면 아래와 같습니다. (여기서 $i$는 허수 $i$가 아닙니다! index입니다!)

IDFT: Inverse Discrete Fourier Transform

• IDFT는 point-value rep.을 coefficient rep.로 바꾸는 변환입니다.
• 이를 수식으로 나타내면 아래와 같습니다.

---

DFT & IDFT

• IDFT는 DFT에서 $\omega^{ki}$ 대신 $\omega^{-ki}$를 쓴 뒤 $n$으로 나누면 됩니다.
• 아래는 참고를 위한 IDFT의 간단한 증명입니다.

using cpx = complex<double>;

void FFT(vector<cpx>& P, bool inv) {
    const int n = P.size();
    if (n == 1) return;
    vector<cpx> A(n / 2), B(n / 2); // P(x) = A(x^2) + x * B(x^2)
    for (int i = 0; i < n / 2; i++) {
        A[i] = P[2 * i];
        B[i] = P[2 * i + 1];
    }
    FFT(A, inv), FFT(B, inv);
    double theta = (inv ? -2 : 2) * acos(-1) / n;
    cpx w(cos(theta), sin(theta)), x(1, 0);
    for (int i = 0; i < n / 2; i++) {
        P[i] = A[i] + x * B[i];
        P[i + n / 2] = A[i] - x * B[i];
        x *= w;
    }
}

비재귀 구현

using cpx = complex<double>;

void FFT(vector<cpx>& P, bool inv = 0) {
	const int n = P.size();
	vector<cpx> root(n / 2);
	for (int i = 1, j = 0; i < n; i++) {
		int bit = n >> 1;
		while (j >= bit) j -= bit, bit >>= 1;
		j += bit;
		if (i<j) swap(P[i], P[j]);
	}
	double ang = (inv ? -2 : 2) * acos(-1) / n;
	for (int i=0; i<n/2; i++) root[i] = cpx(cos(ang * i), sin(ang * i));
	for (int i=2; i<=n; i*=2) {
		for (int j=0; j<n; j+=i) for (int k=0; k<i/2; k++) {
			cpx u = P[j+k], v = P[j+k+ i/2] * root[n/i*k];
			P[j+k] = u+v;
			P[j+k+ i/2] = u-v;
		}
	}
}

NTT: Numerical Theoretical Transform

• 우선 페르마의 소정리를 알고 갑시다.

• 이를 바탕으로 우리는 1의 거듭제곱근을 대체할 방법을 찾을 수 있습니다.

• 소수 $p$를 $2^kb+1$의 형태로 표현한다면 우리는 위 정리를 아래처럼 정리할 수 있습니다.

• 앞선 FFT에서 저희가 $\omega$를 사용했을 때, $\{\omega^0, \omega^1, \cdots, \omega^{n-1}\}$이 모두 다름을 이용했던 걸 기억하시나요?

• 마찬가지로 $p$에 대한 원시근 $g$를 찾는다면, $\omega=g^b$라 할 때, $\{\omega^0, \omega^1, \cdots, \omega^{2^k-1}\}$이 모두 다름을 알 수 있습니다.

• 결과적으로 기존 FFT에서 $\omega$를 $g^{\frac {p-1} N}$으로 치환하면 같은 결과를 얻을 수 있습니다. ($\text{mod}$ 연산이 적용된)

---

void NTT(vector<int> &P, bool inv = 0)
{
    const int n = P.size();
    vector<int> root(n / 2);
    for (int i = 1, j = 0; i < n; i++) {
        int bit = n >> 1;
        while (j >= bit) j -= bit, bit >>= 1;
        j += bit;
        if (i < j) swap(P[i], P[j]);
    }
    for (int i = 0; i < n / 2; i++) // 실제로 이렇게 짜면 시간초과 납니다. 앞 코드와 비슷하게 짜려고 한 부분입니다.
        root[i] = Pow(inv ? Pow(PR, MOD - 2) : PR, (MOD - 1) / n * i);
    for (int i = 2; i <= n; i *= 2)
        for (int j = 0; j < n; j += i)
            for (int k = 0; k < i / 2; k++) {
                int u = P[j + k], v = P[j + k + i / 2] * root[n / i * k] % MOD;
                P[j + k] = (u + v) % MOD;
                P[j + k + i / 2] = (u - v + MOD) % MOD;
            }
    if (inv)
        for (int i = 0, j = Pow(n, MOD - 2); i < n; i++)
            P[i] = P[i] * j % MOD;
}

How about Multivariate Polynomial?

• 잠깐 다변수 다항식에 대해서 생각을 해봅시다.

• $1,x,y,xy$로 이루어진 $P(x,y)$ 라는 다항식이 있다면, 우리는 어떻게 FFT를 적용할 수 있을까요?

• 우선 $y$에 대해 정리해보면 아래와 같은 형태가 됩니다.

  $P(x,y) = Q_0(x)y^0 + Q_1(x)y^1$

• 우리는 각각의 $Q_i(x)$에 대해 FFT를 적용해 $Q_0(1), Q_0(-1), Q_1(1), Q_1(-1)$을 얻을 수 있습니다.

• 그 뒤에, $Q_0(1)y^0 + Q_1(1)y^1$과 $Q_0(-1)y^0 + Q_1(-1)y^1$에 FFT를 적용하면

  $P(1,1),\; P(1,-1),\;P(-1,1),\;P(-1,-1)$

  을 모두 얻을 수 있습니다.

• 다변수 다항식도 똑같이 연산할 수 있구나~ 하고 넘어갑시다.

XOR Convolution

• XOR Convolution은 FFT와 다르게 아래와 같은 연산을 수행합니다.

  $\mathcal{Convolution}: \it\sum_{i+j=k}A_iB_i, \qquad \mathcal{XOR\;Convolution}: \it\sum_{i\oplus j=k}A_iB_i$

• 즉 Convolution에서는 $x^i$와 $x^j$ 간에 연산을 하면 $x^{i+j}$가 됐지만,

• XOR Convolution에서는 $x^i$와 $x^j$ 간에 연산을 하면 $x^{i\oplus j}$가 되어야 합니다.

• 하지만 이 또한 $O(n^2)$이 걸릴 것이고, 이를 $O(n\log n)$에 수행할 수 있도록 하는 변환이 FWHT입니다.

$\{1,2\}$과 $\{2,3\}$간의 모든 XOR 순서쌍을 구하고 싶습니다.

• $P(x) = x^1+x^2$ 와 $Q(x) = x^2+x^3$를 사용하면 결과는 $(P\otimes Q)(x) = x^3+x^2+x^0+x^1$이 돼야 합니다.
• 각 다항식의 지수를 이진수처럼 나타내봅시다.
  $P(x) = x^1+x^2 = x_0^1x_1^0 + x_0^0x_1^1,\qquad Q(x) = x^2+x^3 = x_0^0x_1^1 + x_0^1x_1^1$
• 여기에서 $P(x_0,x_1)$과 $Q(x_0,x_1)$을 곱하고, 지수에 $\text{mod}\;2$를 취해주면 XOR이 되는 걸 볼 수 있습니다.

원래 FFT대로라면 $x_0,x_1$에 $\{1,-1,i,-i\}$를 대입하여 $x_0^2, x_1^2$까지의 결과를 도출하겠지만, $\{1,-1\}$만 대입하면 어떻게 될까요?

• $x_0^2,x_1^2$는 $x_0^0, x_1^0$로 더해지게 됩니다. 이게 우리가 원하는 거죠!

DFT Matrix

• 진짜 마지막으로, 앞서 다뤘던 DFT는 행렬변환으로 나타낼 수 있습니다.
  ${\displaystyle W={\frac {1}{\sqrt {N}}}{\begin{bmatrix}1&1&1&1&\cdots &1\\1&\omega &\omega ^{2}&\omega ^{3}&\cdots &\omega ^{N-1}\\1&\omega ^{2}&\omega ^{4}&\omega ^{6}&\cdots &\omega ^{2(N-1)}\\1&\omega ^{3}&\omega ^{6}&\omega ^{9}&\cdots &\omega ^{3(N-1)}\\\vdots &\vdots &\vdots &\vdots &\ddots &\vdots \\1&\omega ^{N-1}&\omega ^{2(N-1)}&\omega ^{3(N-1)}&\cdots &\omega ^{(N-1)(N-1)}\end{bmatrix}}},\quad W=W^{-1}$
• 여기까지가 FWHT: Fast Walsh-Hadamard Transform의 이론적 배경입니다.

---

FWHT: Fast Walsh-Hadamard Transform

• 지금까지의 부분을 빠르게 계산하기 위해서 아다마르 변환(Hadamard Transform)을 사용합니다.

• 아다마르 변환 $H_m$은 $2^m \times 2^m$ 행렬이며 다음과 같이 정의됩니다. (원래는 앞에 $1/\sqrt 2$가 붙습니다.)

  ${\displaystyle H_{m}={\begin{pmatrix}H_{m-1}&H_{m-1}\\H_{m-1}&-H_{m-1}\end{pmatrix}},\quad\displaystyle H_{1}={\begin{pmatrix}1 &1\\1 &-1\end{pmatrix}}}$

• 그 형태를 잘 보면 $\omega$로 -1만을 사용하는 DFT 행렬인걸 볼 수 있습니다.

• 행렬변환이기 때문에 역변환도 행렬로 나타납니다. ($1/\sqrt 2$가 있다면 $H_m$과 같았겠죠?)

  ${\displaystyle H_{m}^{-1}=\frac{1}{2^m}H_m}$

• 이제 저 재귀적인 형태를 그대로 구현하면 FWHT를 구현할 수 있습니다.

---

FWHT: Fast Walsh-Hadamard Transform

void FWHT(vector<int>& P, bool inv = 0) {
    const int n = P.size();
    for (int i=2; i<=n; i*=2) {
        for (int j=0; j<n; j+=i) {
            for (int k=0; k<i/2; k++) {
              int u = P[j+k], v = P[j+k+ i/2];
              P[j+k] = u+v;
              P[j+k+ i/2] = u-v;
              if(inv) P[j+k]/=2, P[j+k+ i/2]/=2;
            }
        }
    }
}

---

BOJ Examples

FFT

• 1067. 이동
• 5051. 피타고라스의 정리

NTT

• 14882. 다항식과 쿼리

FWHT

• 14878. 부분수열 XOR합
• 25563. AND, OR, XOR

---

저자의 코드

FFT, NTT의 코드는 큰 수 곱셈 (3)에 제출된 코드입니다.

• FFT
• NTT

FWHT의 코드는 Just as Tic Tac Toe에 제출된 코드입니다.

• FWHT

Appendix. Good Primes for NTT

• NTT 알고리즘을 살펴보면 $p-1$이 꽤 큰 2의 제곱인수를 가져야 하는 걸 알 수 있습니다.

• 예를 들어 $998,244,353$은 $2^{23} \times 119 + 1$로, N이 $2^{23}$ 일 때까지 사용할 수 있습니다.

• 아래는 NTT를 위한 좋은 소수들을 소개합니다. ($p = a\cdot 2^b$, $w$는 $p$의 원시근)

  $p$	$a$	$b$	$w$
  998,244,353	119	23	3
  2,281,701,377	17	27	3
  2,483,027,969	37	26	3
  2,113,929,217	63	25	5
  104,857,601	25	22	3
  1,092,616,193	521	21	3

Appendix. NTT for Arbitrary modulos

• 좋은 소수들이 있어도, 문제에서 $1e9+7$로 나눈 나머지를 구하세요! 라고 하면 못씁니다.

  중국인의 나머지 정리(Chinese Remainder Theorem, CRT)
  $m_1, m_2, \cdots, m_n$이 서로소라면, 다음 연립합동식

  $x ≡ \begin{cases} a_1 &\mod m_1\\ a_2 &\mod m_2\\ &\vdots\\ a_n &\mod m_n \end{cases}$

  는 $\displaystyle \text{mod}\;\prod^{n}_{i=1}m_i$에 대하여 유일한 해를 갖는다.

• 이 말인 즉슨, $\text{mod}\;998,244,353 \times 2,281,701,377 \times \cdots$에 대해서 유일한 해를 구할 수 있다는 것이고, 이건 대체로 문제에서 실제 해에 해당합니다. (확장된 유클리드 알고리즘으로 계산할 수 있습니다.)

• 적당히 큰 소수 몇 개에 대해서 NTT를 수행한 다음 주어진 소수로 나눠주면 됩니다.