Markov Decision Processes (MDP)
- MDP는 Fully observable한 환경에서, 강화학습을 위한 환경을 묘사한다.
- 즉, 현재 상태가 완전하게 과정을 특징한다.
- 대부분의 RL 문제들은 MDP로 정리할 수 있다.
- Partially observable problem도 MDP로 변환될 수 있다.
Markov Property
- 현재 상태를 안다면 미래와 과거는 독립적이다
- 상태는 역사로부터 모든 관련있는 정보들을 포집한다.
- 상태가 알려져있다면, 역사는 갖다 버려도 된다.
Markov Process
- Markov process는 memoryless한 random process이다.
Definition: Markov Process
Markov Process (또는 Markov Chanin)은 순서쌍 (S,P)이다.
- S는 유한한 상태들의 집합이다.
- P는 상태 전이 확률분포 행렬이다.
Pss′=P[St=s′∣St=s]
State Transition Matrix
- 마르코프 상태 S와 후속 상태 S′에 대해, 상태 전이 확률은 다음과 같이 정의된다.
Pss′=P[St=s′∣St=s]
- 상태 전이 행렬 P는 모든 전이 확률들을 포함한다.
P=from⎣⎢⎢⎡P11⋮Pn1……P1n⋮Pnn⎦⎥⎥⎤to
- 각 열의 합은 1이다.
Markov Reward Process
Markov reward process는 values(rewards)를 포함하는 Markov chain이다.
Definition: Markov Reward Process
Markov Reward Process은 순서쌍 (S,P,R,γ)이다.
- S는 유한한 상태들의 집합이다.
- P는 상태 전이 확률분포 행렬이다.
Pss′=P[St=s′∣St=s]
- R은 reward function으로, Rs=E[Rt+1∣St=s]이다.
- γ는 discount factor로, γ∈[0,1] 이다.
(Discounted) Return
Definition: Return
Return Gt는 time step t부터의 총 discounted reward를 의미한다.
Gt=Rt+1+γRt+2+⋯=k=0∑∞γkRt+k+1
- γ는 현재의 보상을 지연된 보상보다 얼마나 중요시할지를 의미한다.
- γ가 0에 가까울 수록 근시안적,
- γ가 1에 가까울 수록 원시안적이다.
Discount factor를 사용하는 이유
- 순환하는 Markov process에서 무한한 return을 피하기 위해
- 미래에 대한 불확정성이 충분히 표현되지 않았을 수 있으므로
- 만약 보상이 금전적이라면 당장의 보상이 지연된 보상보다 더 중요하므로
- 인간과 동물은 당장의 보상을 더 선호하므로
Value Function
- value function v(s)는 s로부터의 long-term value를 계산한다.
- MRP의 state value function은 s로 부터 시작할 때 return의 기댓값이다.
v(s)=E[Gt∣St=s]
Bellman Equation for MRPs
- Value function은 두 파트로 나뉘어질 수 있다.
- 당장의 보상 Rt+1
- 후속 상태의 할인된 보상 γV(St+1)
v(s)=E[Gt∣St=s]=E[Rt+1+γRt+2+γ2Rt+3+⋯∣St=s]=E[Rt+1+γ(Rt+2+γRt+3+…)∣St=s]=E[Rt+1+γGt+1∣St=s]=E[Rt+1+γv(St+1)∣St=s]=Rs+γs′∈S∑Pss′v(s′)
- Bellman equation은 V가 각 상태별로 하나의 요소만 갖는 열벡터일때, 행렬들을 이용해서 더 간결하게 표현될 수 있다.
V=R+γPV
⎣⎢⎢⎡v(1)⋮v(n)⎦⎥⎥⎤=⎣⎢⎢⎡R1⋮Rn⎦⎥⎥⎤+γ⎣⎢⎢⎡P11⋮P11………P1n⋮Pnn⎦⎥⎥⎤⎣⎢⎢⎡v(1)⋮v(n)⎦⎥⎥⎤
Solving the Bellman Equation
- 벨만 방적식은 선형방정식으로 직접적으로 풀 수 있다.
v(1−γP)vv=R+γPv=R=(1−γP)−1R
- 시간복잡도는 N 개의 상태에 대해 O(N3)이고,
- 이는 작은 MRP에 대해서만 가능하다.
- 큰 MRP에 대해서는 다음과 같은 iterative method 들이 있다.
- Dynamic programming
- Monte-Carlo evaluation
- Temporal-Difference learning
Markov Decision Process
Markov decision process는 decision이 있는 Markov reward process이다.
Definition: Markov Decision Process
Markov Decision process은 순서쌍 ⟨S,A,P,R,γ⟩이다.
- S는 유한한 상태들의 집합이다.
- A는 유한한 행동들의 집합이다.
- P는 상태 전이 확률 행렬이다.
Pss′a=P[St=s′∣St=s,At=a]
- R은 reward function으로, Rsa=E[Rt+1a∣St=s,At=a]이다.
- γ는 discount factor로, γ∈[0,1] 이다.
Policies
Definition: Policy
Policy π는 주어진 상태에 대한 행동들의 분포이다.
π(a∣s)=P[At=a∣St=s]
- 정책은 에이전트의 행동을 완전히 정의한다.
- MDP 정책은 현재 상태 (not history)에 의해 결정된다.
- 즉, 정책은 시간에 독립적이다. At∼π(⋅∣St),∀t>0
- MDP = ⟨S,A,P,R,γ⟩와 정책 π가 정해졌을 때,
- 상태 시퀀스 S1,S2,…는 Markov process ⟨S,Pπ⟩이다.
- 상태와 리워드 시퀀스 S1,R2,S2,…는 Markov reward process ⟨S,Pπ,Rπ,γ⟩이다.
Ps,s′πRsπ=a∈A∑π(a∣s)Pss′a=a∈A∑π(a∣s)Rsa
Value Function
Definition: State-Value Function
state-value function vπ(s)는 s상태에서 π 정책을 따를 때의 return의 기댓값이다.
vπ(s)=Eπ[Gt∣St=s]
Definition: Action-Value Function
action-value function qπ(s,a)는 s상태에서 a 행동을 취했고, π 정책을 따를 때의 return의 기댓값이다.
qπ(s,a)=Eπ[Gt∣St=s,At=a]
Bellman Expectation Equation
- State-value function은 당장의 리워드와 후속상태의 할인된 리워드로 분해될 수 있다.
vπ(s)=Eπ[Rt+1+γvπ(St+1)∣St=s]
- Action-value function도 비슷하게 분해될 수 있다.
qπ(s,a)=Eπ[Rt+1+γqπ(St+1,At+1)∣St=s,At=a]
Bellman Expectation Equation for Vπ
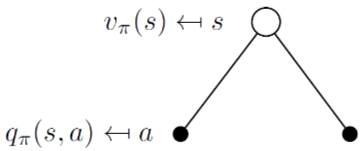
vπ(s)=a∈A∑π(a∣s)qπ(s,a)(1)
(3) 참고
vπ(s)=a∈A∑π(a∣s)(Rsa+γs′∈S∑Pss′avπ(s′))(2)
Bellman Expectation Equation for Qπ
qπ(s,a)=Rsa+γs′∈S∑Pss′avπ(s′)(3)
qπ(s,a)=Rsa+γs′∈S∑Pss′aa′∈A∑π(a′∣s′)qπ(s′,a′)(4)
Vπ=Rπ+γPπVπ
(1) 참고
Vπ=(I−γPπ)−1Rπ
Optimal Value Function
Optimal value function은 MDP에서 가능한 가장 좋은 성능을 말해주므로, 우리가 Optimal value function을 안다면 MDP가 해결되었다고 할 수 있음.
Definition Optimal value function
optimal state-value function v∗(s)은 모든 정책 중 가장 큰 maximum state-value function을 의미함
v∗(s)=πmaxvπ(s)
optimal action-value function q∗(s,a)는 가장 큰 action-value function을 의미함
q∗(s,a)=πmaxqπ(s,a)
Optimal policy
π가 모든 state에 대해 return의 기댓값이 π′보다 크거나 같다면, π가 π′보다 좋거나 같다.
π≥π′ if vπ(s)≥vπ′(s),∀s
Theorem
임의의 Markov Decision Process에 대해
- optimal policy π∗가 존재한다면, 존재하는 모든 다른 π에 대해 π∗≥π,∀π이다.
- 모든 optimal policy는 optimal value function을 달성한다. vπ∗(s)=v∗(s)
- 모든 optimal policy는 optimal action-value function을 달성한다. qπ∗(s,a)=q∗(s,a)
Finding an Optimal Policy
- Optimal policy는 q∗(s,a) 를 최대화하는 방향으로 찾을 수 있다.
π∗(a∣s)={10ifa=argmaxa∈Aq∗(s,a)otherwise
- 어떤 MDP던 결정론적 optimal policy가 존재한다.
- 만약 우리가 q∗(s,a)를 안다면 즉시 optimal policy를 알 수 있다.
Bellman Optimality Equation for v∗
v∗(s)=amaxq∗(s,a)(5)
(7) 참고
vπ(s)=amax(Rsa+γs′∈S∑Pss′av∗(s′))(6)
Bellman Optimality Equation for q∗
qπ(s,a)=Rsa+γs′∈S∑Pss′av∗(s′)(7)
qπ(s,a)=Rsa+γs′∈S∑Pss′aamaxq∗(s,a)(8)