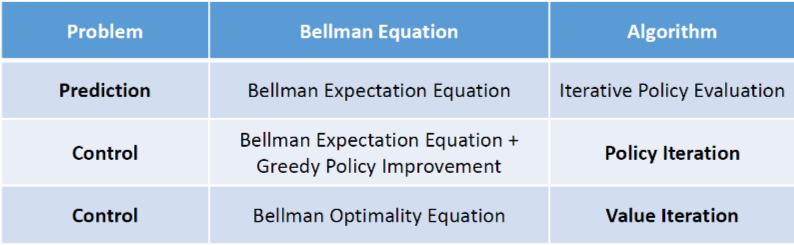
Planning and Learning
Planing: 환경의 model을 아는 상태에서, 그 모델과만 상호작용하며 policy를 개선하는 것
Requirements for Dynamic Programming
다이나믹 프로그래밍을 위해 두가지 특징이 필요하다.
- Optimal substructure
- Principle of optimality가 적용되어야 함
- Optimal solution이 subproblem들로 나누어질 수 있음
- Overlapping subproblems
- subproblem들은 여러번 다시 발생함
- solution들이 캐시되고, 재사용될 수 있음.
Markov decision process들은 이 두 속성을 모두 만족함
- bellman equation은 재귀적 분할을 가능하게 함
- value function은 solution을 저장하고 재사용함
Planning by DP
MDP의 모든 정보를 알고 있다고 가정함
prediction에서:
- input: MDP ⟨S,A,P,R,γ⟩와 정책 π
- output: value function vπ
control에서:
- input: MDP ⟨S,A,P,R,γ⟩
- output: optimal value function v∗와 optimal policy π∗
Iterative Policy Evaluation
주어진 policy π를 평가하는 법:
- bellman expectation의 반복적인 계산으로 할 수 있다!
각 k+1 번째 반복마다,
모든 상태 s∈S에 대해
vk+1(s)를 vk(s′)로부터 업데이트함.
vk+1(s)≐Eπ[Rt+1+γvk(St+1)∣St=s]=a∑π(a∣s)s′,r∑p(s′,r∣s,a)[r+γvk(s′)]
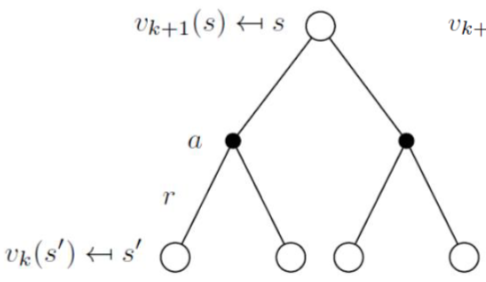
k가 ∞으로 커짐에 까라 vk는 vπ로 수렴할 수 있다.
Algorithm: Iterative Policy Evaluation
- 입력 π에 대해
- estimation 정확도를 결정하는 작은 역치값 θ>0와 함께
- V(s)를 모든 s∈S+에 대해 초기화하고,
- 다음을 Δ<θ까지 반복한다.
- Δ←0
- 모든 s∈S에 대해 반복:
- v←V(s)
- V(s)←∑aπ(a∣s)∑s′,rp(s′,r∣s,a)[r+γV(s′)]
- Δ←max(Δ,∣v−V(s)∣)
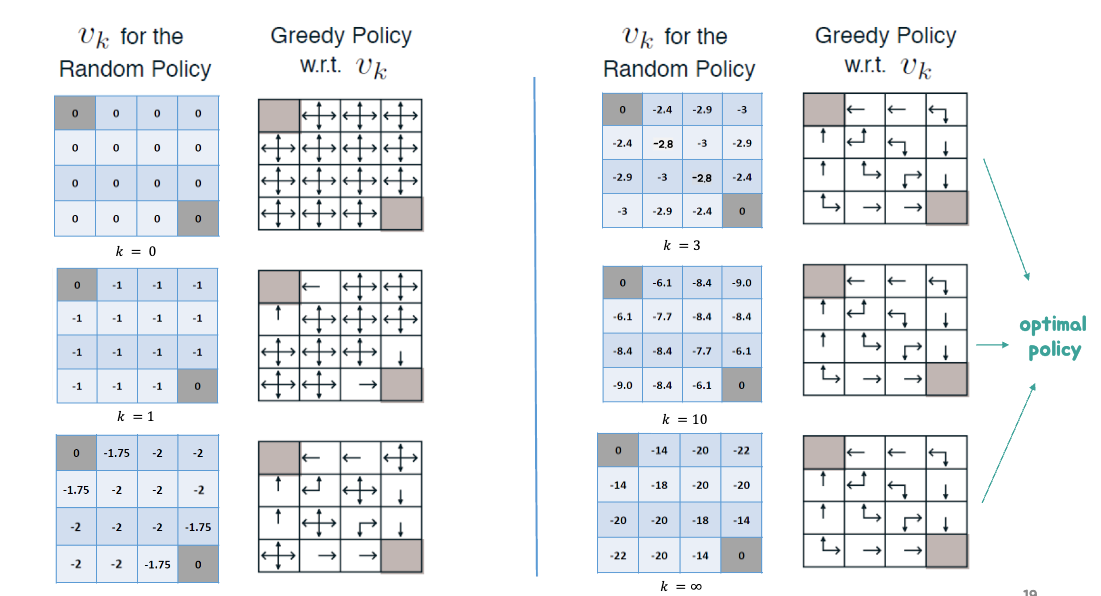
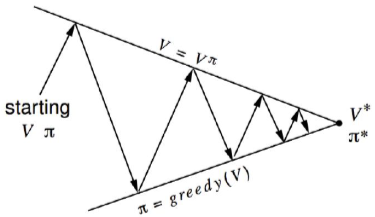
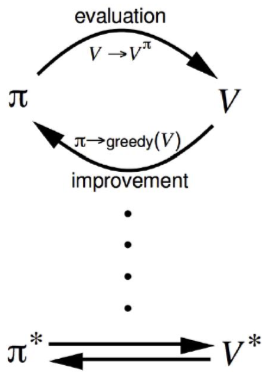
Policy Iteration
- Policy π가 주어졌을 때,
- π를 평가하고
vπ(s)=E[Rt+1+γRt+2+…∣St=s]
- vπ에 따라 그리디하게 행동하도록 정책을 업데이트한다.
π′=greedy(vπ)
- policy iteration은 항상 최적의 정책 π∗로 수렴함.
Policy Improvement
- 결정론적인 정책 a=π(s)가 주어졌을 떄,
- 우리는 그리디하게 행동함으로써 정책을 업데이트할 수 있다.
π′(s)=greedy(vπ)=a∈Aargmaxqπ(s,a)
- 이는 매 스텝마다 모든 상태 S에 대한 value들을 개선한다.
qπ(s,π′(s))=a∈Amaxqπ(s,a)≥qπ(s,π(s))=vπ(s)
- 그러면 이 부등식이 만족할까?
vπ′(s)≥vπ(s)
Proof
qπ(s,a)≐E[Rt+1+γvπ(St+1)∣St=s,At=a]=s′,r∑p(s′,r∣s,a)[r+γvπ(s′)].(4.6)
qπ(s,π′(s))≥vπ(s).(4.7)
vπ(s)≤qπ(s,π′(s))=E[Rt+1+γvπ(St+1)∣St=s,At=π′(s)]=Eπ′[Rt+1+γvπ(St+1)∣St=s]≤Eπ′[Rt+1+γqπ(St+1,π′(St+1))∣St=s]=Eπ′[Rt+1+γEπ′[Rt+2+γvπ(St+2)∣St+1,At+1=π′(St+1)]∣St=s]=Eπ′[Rt+1+γRt+2+γ2vπ(St+2)∣St=s]≤Eπ′[Rt+1+γRt+2+γ2Rt+3+γ3vπ(St+3)∣St=s]⋮≤Eπ′[Rt+1+γRt+2+γ2Rt+3+γ3Rt+4+⋯∣St=s]=vπ′(s).
만약 개선이 멈춘다면,
qπ(s,π′(s))=a∈Amaxqπ(s,a)=qπ(s,π(s))=vπ(s)
를 만족하고, Bellman optimality equation또한 만족한다.
vπ(s)=a∈Amaxqπ(s,a)
따라서 모든 s∈S에 대해 vπ(s)=v∗(s)가 만족한다.
따라서 π가 optimal poilicy이다.
Algorithm: Policy Iteration

Modified Policy Iteration
- policy evaluation이 매번 vπ로 수렴해야 할까?
- 아니면 우리가 정지조건을 만들 수 있을까?
- k번 반복 후 policy evaluation을 해도 되지 않을까?
- 아니면 그냥 매 반복마다 policy를 업데이트 해도 되지 않을까? == value iteration
Value Iteration
Optimal policy를 찾기 위해
- 각 k+1번째 반복마다
- 모든 상태 s∈S에 대해
- vk(s′)로부터 vk+1(s)를 업데이트한다.
vk+1(s)≐amaxE[Rt+1+γvk(St+1∣St=s,At=a]=amaxs′,r∑p(s′,r∣s,a)[r+γvk(s′)]
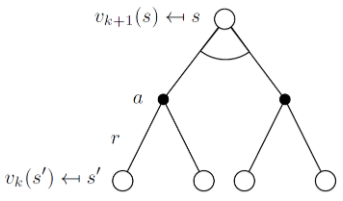
vk+1(s)vk+1=a∈Amax(Rsa+γs′∈S∑Pss′avk(s′))=a∈AmaxRa+γPavk

요약
알고리즘들은 state-value function을 기반으로 하고 있으며, m개의 action과 n개의 상태에 대해 iteration당 O(mn2)가 필요하다.
action-state-value function에 대해서는 반복당 O(m2n2)가 필요하다.