VII. Normalization

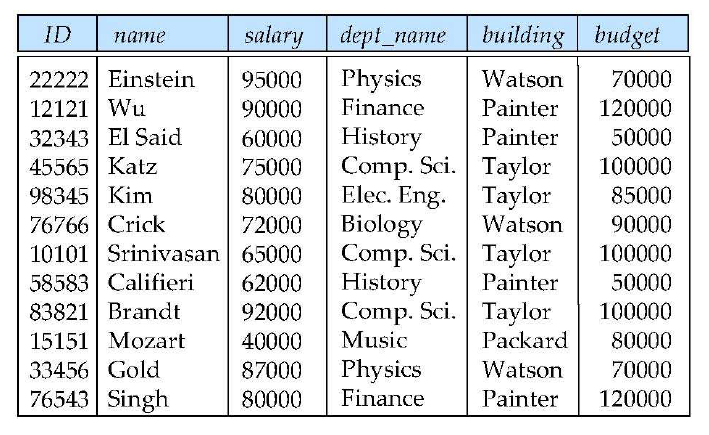
Functional Dependency

inst_dept

• funtional dependency:
  dept_name $\rarr$ building, budget
• inst_dept에서 dept_name은 후보키가 아니지만 budget은 dept_name에 의존함.
• 즉, building,budget이 불필요하게 중복되고 있음
  • Decompose!

Decomposition

• 우리는 다시 원래 relation을 복구할 수 있어야 함.
• 만약 동명이인 등의 이유로 복구할 수 없다면 lossy decomposition이 됨

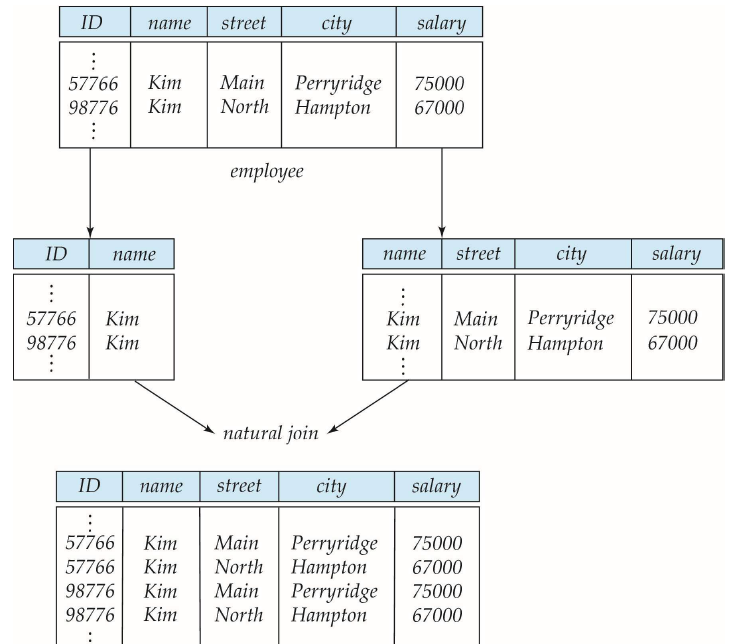
Lossless-join Decomposition

• 우리는 R을 $R_1 \cup R_2$로 대체했을 때, 정보의 손실이 없으면 lossless decomposition이라고 부름

• 그리고 역으로 다음 경우에 lossy라고 할 수 있음

Normalization Theory

• 우리는 특정 relation $R$이 좋은 형태인지 결정해야 함
• 만약 좋은 형태가 아니라면 $\{R_1, R_2, \dots, R_n\}$으로 분해해야함.
  • s.t. 각 relation이 좋은 형태이고
  • 분해는 lossless-join decomposition이도록.

Functional Dependencies

• $R$이 relation schema라고 할 때, ($\alpha, \beta$는 attribute들의 집합)

• $\alpha \rarr \beta$ (alpha determines beta) functional dependency가 성립한다.
  $\Lrarr$

• 임의의 relation $r(R)$에 대해서 $t_1$과 $t_2$가 $\alpha$와 $\beta$에 대해

  $t_1 [\alpha] = t_2[\alpha] \Rarr t_1 [\beta] = t_2[\beta]$

• Functional dependency는 key의 정의를 일반화한것임

• $K$가 superkey $\Lrarr$ $K \rarr R$

• $K$가 후보키 $\Lrarr$

  • $K \rarr R$ and
  • $\forall \alpha \subset K, \text{no} (K-\alpha) \rarr R$

• $\alpha \rarr \beta$는 $\alpha \supseteq \beta$일때 자명함

Closure of a Set of Functional Dependencies

• Functional dependency는 추론규칙이 성립함
  • $A \rarr B,B\rarr C$라면 $A\rarr C$임
• $F$로부터 논리적으로 얻을 수 있는 모든 functional dependency의 집합을 $F$의 closure이라고 부름
• $\textsf{\textbf{F}}^+$ 라고 표기함
• $\textsf{\textbf{F}}^+$는 F의 superset임

• $\textsf{\textbf{F}}^+$는 Armstrong's Axiom을 반복하여 얻을 수 있음
  • reflexivity: $\beta \subseteq\alpha \Rarr \alpha\rarr\beta$
  • augmentation: $\alpha\rarr\beta \Rarr \gamma\alpha\rarr\gamma\beta$
  • transitivity: $\alpha\rarr\beta$ and $\beta\rarr\gamma \Rarr\alpha\rarr\gamma$

• 추가적인 규칙
  • union: $\alpha\rarr\beta$ and $\alpha\rarr\gamma\Rarr\alpha\rarr\beta\gamma$
  • decomposition: $\alpha\rarr\beta\gamma\Rarr\alpha\rarr\beta$ and $\alpha\rarr\gamma$
  • pseudotransitivity: $\alpha\rarr\beta$ and $\gamma\beta\rarr\delta\Rarr\alpha\gamma\rarr\delta$

Dependency preservation

$F_i$가 $\textsf{\textbf{F}}^+$의 $R_i$에 대한 denpendency라면

• 아래를 만족할 경우 dependency preserving이다.

Boyce-Codd Normal Form(BCNF)

• $\textsf{\textbf{F}}^+$의 임의의 dependency $\alpha\rarr\beta$가 다음 둘 중 하나를 만족한다면,
  • $\alpha\rarr\beta$가 자명하거나
  • $\alpha$가 R의 superkey
• R은 BCNF이다.

• 위의 예시 inst_dept (ID, name, salary, dept_name, building, budget )의 경우 dept_name -> building,budget을 만족하고, dept_name이 superkey가 아니므로, BCNF가 아님

• 이 경우 R을
  • $\alpha\cup\beta$
  • $R-(\beta-\alpha)$
• 로 분해할 수 있음.

BCNF may decompose "too much"

• BCNF가 항상 dependency preservation을 지키는 것은 아님.
• dept_advisor(s_ID, i_ID, department_name)에서
  • i_ID -> dept_name
  • s_ID,dept_name -> i_ID
    가 성립함
• i_ID는 superkey가 아니므로 dept_advisor는 BCNF가 아님
• 그러나 어떤 decomposition이더라도
  s_ID,dept_name -> i_ID
  이 dependency는 지킬 수가 없음
• 즉, 우리는 더 약한 normal form이 필요함 - 3NF

Third Normal Form (3NF)

• 약간의 중복을 허용함

• 항상 lossless-join, dependency-preserving만 함

• $\textsf{\textbf{F}}^+$의 임의의 dependency $\alpha\rarr\beta$가 다음 둘 중 하나를 만족한다면,

  • $\alpha\rarr\beta$가 자명하거나
  • $\alpha$가 R의 superkey 이거나
  • (추가) $\beta-\alpha$의 각 attribute$A$가 후보키에 포함되어 있다.

• R은 3NF이다.

• 만약 BCNF라면 3NF임.

• 이 세번째 조건은 dependency preservation을 만족하기 위한 최소한의 완화조건임.

Comparison of BCNF and 3NF

• 3NF의 장점
  • 항상 lossless join과 dependency preservation을 희생하지 않고 3NF를 얻는 것이 가능하다.
• 단점
  • 몇몇 의미있는 relationship을 표현하기 위해 null을 써야 할 수 있음
  • 정보의 중복이 발생함

정규화의 목표

• 더 적은 저장 공간
• 더 빠른 업데이트
• 더 적은 데이터 불일치
• 더 깨끗한 데이터 relationships
• 더 쉬운 데이터 추가
• 더 유연한 구조

설계 목표

관계형DB의 목표는

• BCNF
• Lossless join
• Dependency preservation

이걸 달성하지 못한다면 우리는

• dependency preservation의 부족이나
• 3NF 사용으로 인한 redunduncy를 받아들여야 함

SQL은 superkey를 제외하고는 functional dependency를 표현할 방법을 제공하지 않음
SQL에서 우리는 LHS가 key가 아닌 경우 functional dependency를 효율적으로 검사할 수 없음.

전반적인 DB 설계 과정

• 스키마 $R$을 갖고 있을 때
  • $R$은 모든 attribute를 갖는 하나의 relation일 수 있음
  • 정규화는 이를 더 작은 relation들로 분해함
• ERD가 잘 설계되었다면 테이블들은 더이상의 정규화를 필요로하지 않음
• 하지만 실제 설계에서는 non-key attrebute로부터의 functional dependency가 발생할 수 있음

성능을 위한 Denormalization

• 성능을 위해 non-normalized schema를 사용할 수 있음
• Join은 가장 비싼 연산임
• 여기에서 두가지 대안이 있음

1. denormalized relation을 사용하기
2. Materialized view(query의 결과를 모두 보관하는 물리적 table)를 course $\bowtie$ prereq로 보관하기