
트리
노드와 링크로 구성된 자료구조(그래프 일종, Cycle 없음 : 있으면 그래프)
계층적 구조를 나타낼때 사용
- 폴더 구조(디렉토리, 서브 디렉토리)
- 조직도, 가계도 ...
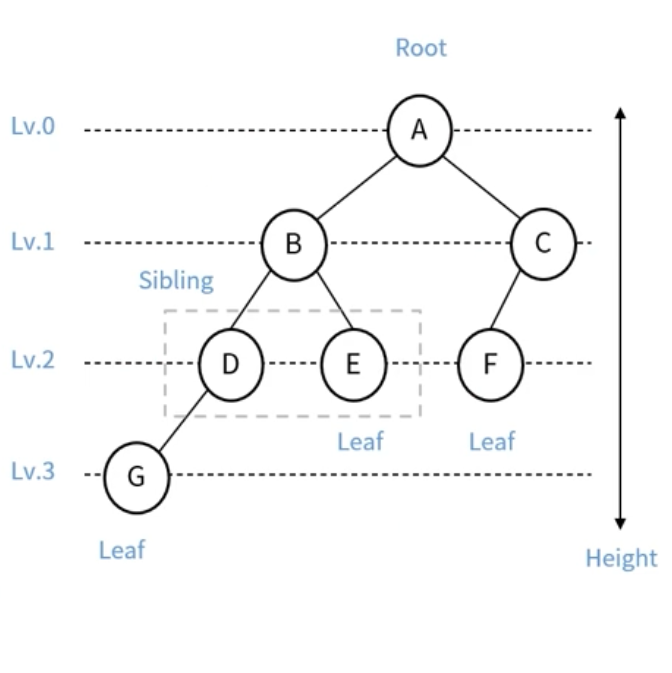
노드(Node): 트리 구조의 자료값을 담고 있는 단위엣지(Edge): 노드 간의 연결선(== link, Branch)루트 노드(Root): 부모가 없는 노드, 가장 위의 노드리프 노드(Leaf): 자식이 없는 노드(=단말)내부 노드(Internal): 리프 노드를 제외한 모든 노드부모(Parent): 연결된 두 노드 중 상위 노드자식(Child): 연결된 두 노드 중 하위의 노드형제(Sibling): 같은 부모를 가지는 노드깊이(Depth): 루트에서 어떤 노드까지의 간선의 수레벨(Level): 트리의 특정 깊이를 가지는 노드 집합높이(Height): 트리에서 가장 큰 레벨 값크기(Size): 자신을 포함한 자식 노드의 개수차수(Degree): 각 노드가 지닌 가지의 수트리의 차수: 트리의 최대 차수
특징
- 하나의 노드에서 다른 노드로 이동하는 경로는 유일
- 노드가 N개인 트리의 Edge수는 N-1개
- Acyclic(Cycle이 존재하지 않음)
- 모든 노드는 서로 연결되어 있음
- 하나의 Edge를 끊으면 2개의 Sub-Tree로 분리됨
이진 트리(Binary Tree)
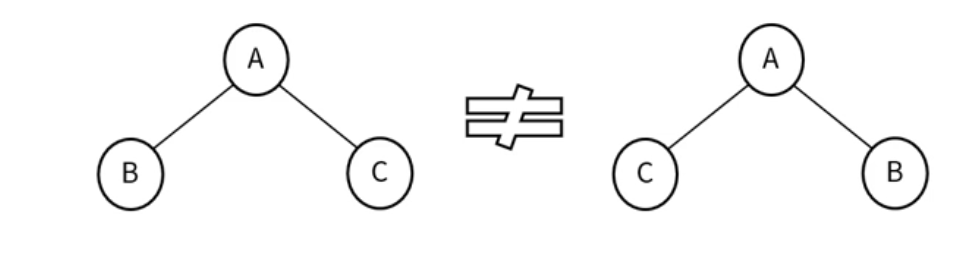
각 노드는 최대 2개의 자식을 가질 수 있음
자식 노드는 좌우를 구분함
-> 왼쪽 자식 : 부모 노드의 왼쪽 아래
-> 오른쪽 자식 : 부모 노드의 오른쪽 아래
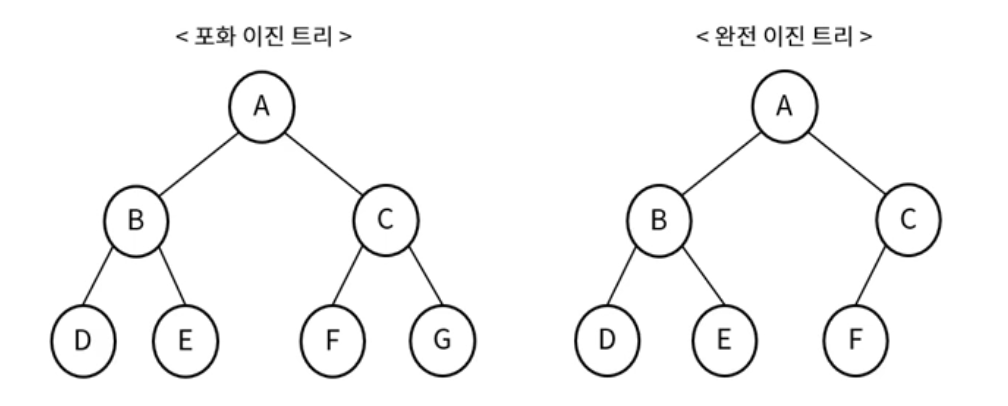
포화이진트리(Perfect Binary Tree) : 모든 레벨에서 노드들이 꽉 채워져 있는 트리
완전이진트리(Complete Binary Tree) : 마지막 레벨을 제외하고 노드들이 모두 채워져 있는 트리
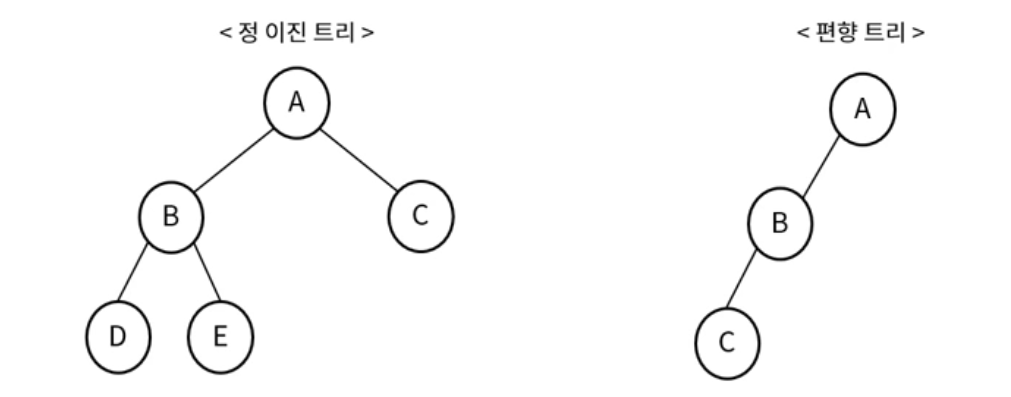
정 이진 트리 (Full binary Tree) : 모든 노드가 0개 또는 2개의 자식 노드를 갖는 트리
편향 트리 (Skewed Binary Tree) : 한쪽으로 기울어진 트리
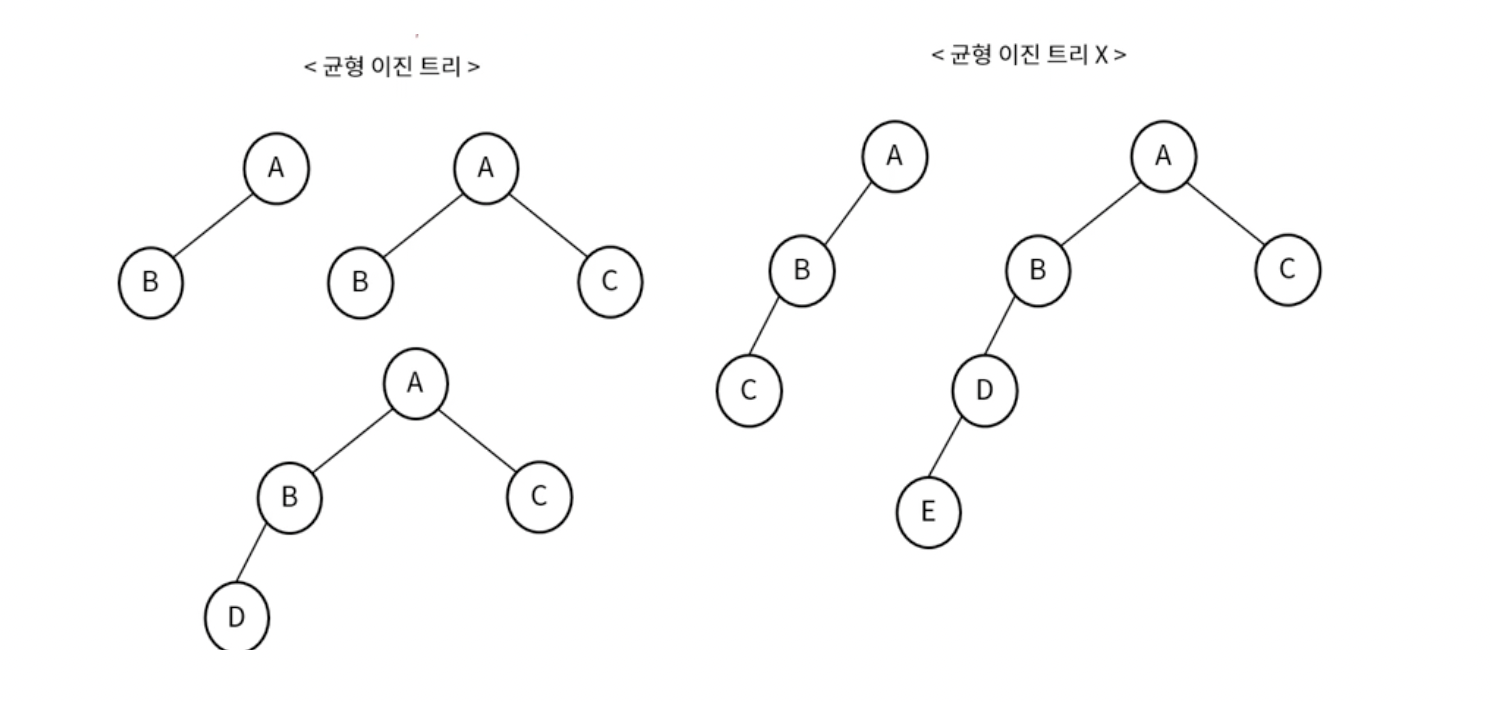
균형 이진 트리(Balanced Binary Tree) : 모든 노드의 좌우 서브 트리 높이(트리에서 가장 큰 레벨 값)가 1이상 차이가 나지 않는 트리
-> 균형 이진 트리가 아닌 것 보다 균형 이진 트리는 탐색 속도가 빠름
이진 트리 특징
포화 이진 트리의 높이가 h일때 -> 노드의 수는 Math.pow(2, h+1) - 1
포화 (or 완전) 이진 트리의 노드가 N개 일대, 높이는 logN(소숫점은 버림)
이진 트리의 노드가 N개 일때, 최대 가능 높이는 N-1(편향 트리인 경우)
이진 트리 순회(Traversal)
모든 노드를 빠뜨리거나 중복하지 않고 방문하는 연산
순회 종류 4가지
전위 순회, 중위 순회, 후위 순회 -> DFS의 일종
레벨 순회 -> BFS의 일종
전위 순회(PreOrder Traversal)
현재 노드 -> 왼쪽 노드 -> 오른쪽 노드
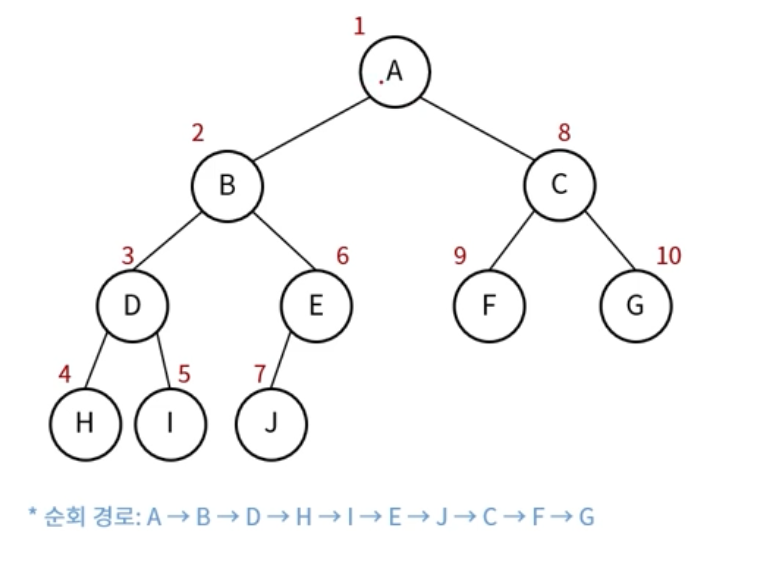
중위 순회(InOrder Traversal)
왼쪽 노드 -> 현재 노드 -> 오른쪽 노드
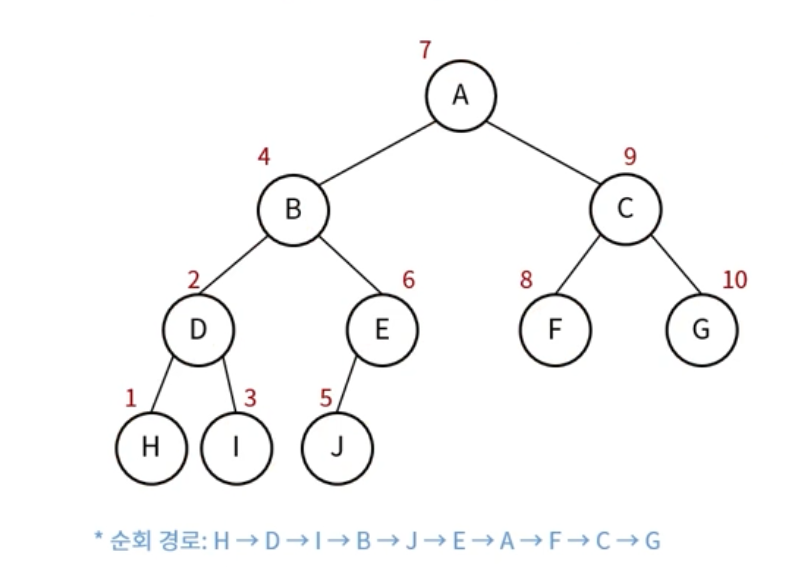
후위 순회(PostOrder Traversal)
왼쪽 노드 -> 오른쪽 노드 -> 현재 노드
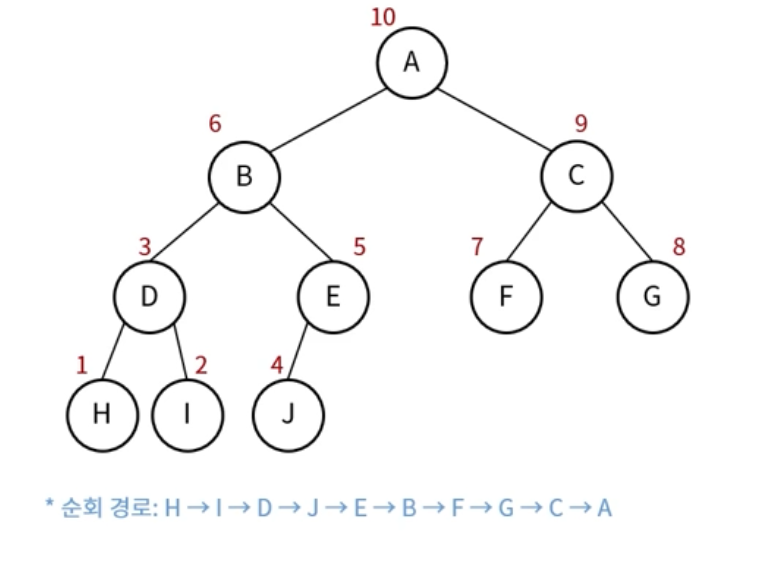
레벨 순회(Levelorder Traversal)
위쪽 레벨부터 왼쪽 노드 -> 오른쪽 노드
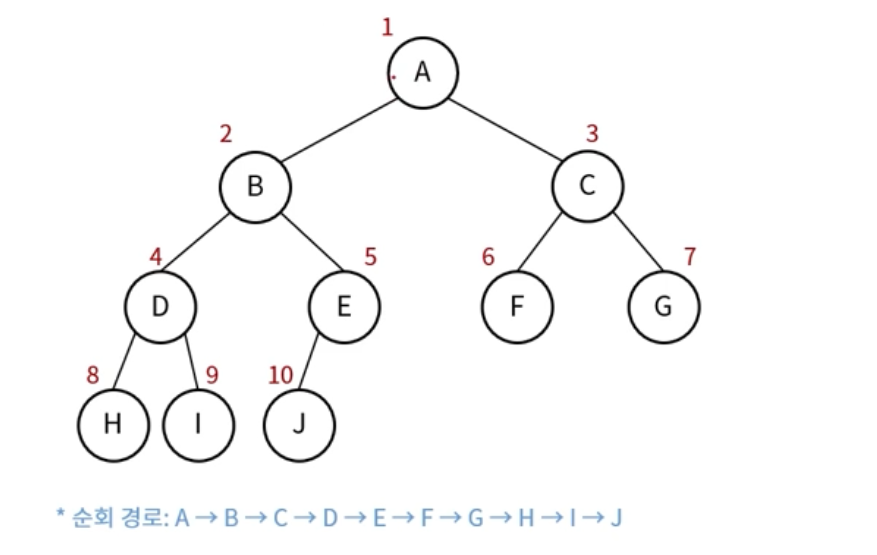
이진 트리 구현
배열 : 레벨 순회 순으로 배열에 구성
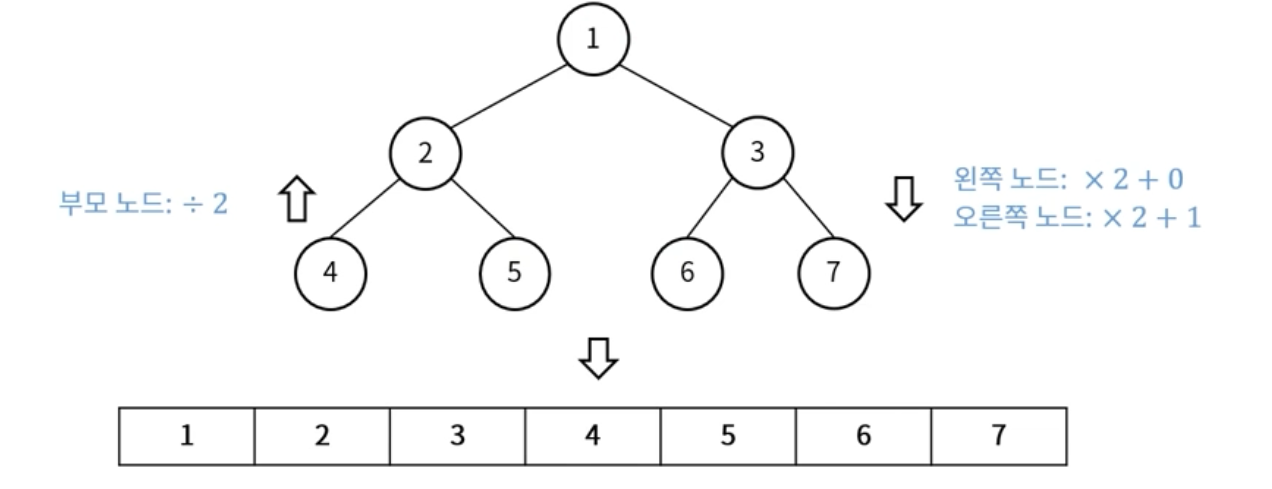
위 그림은 배열의 인덱스가 1부터 시작한다 가정
연결리스트 사용 시 -> 값과 간선을 관하기 위한 노드로 연결리스트 구성(next가 2개 있다고 생각하자)
배열을 이용한 이진 트리 구성 및 순회 구현
// 배열을 이용한 이진 트리 구성, 순회
class BinaryTree{
char[] arr;
BinaryTree(char[] data){
this.arr = data.clone();
}
public void preOrder(int idx){
System.out.print(this.arr[idx] + " ");
int left = 2 * idx + 1;
int right = 2 * idx + 2;
if(left < this.arr.length){
this.preOrder(left);
}
if(right < this.arr.length){
this.preOrder(right);
}
}
public void inOrder(int idx){
int left = 2 * idx + 1;
int right = 2 * idx + 2;
if(left < this.arr.length){
this.inOrder(left);
}
System.out.print(this.arr[idx] + " ");
if(right < this.arr.length){
this.inOrder(right);
}
}
public void postOrder(int idx){
int left = 2 * idx + 1;
int right = 2 * idx + 2;
if(left < this.arr.length){
this.postOrder(left);
}
if(right < this.arr.length){
this.postOrder(right);
}
System.out.print(this.arr[idx] + " ");
}
public void levelOrder(int idx){
for(int i = 0; i < this.arr.length; i++){
System.out.print(this.arr[i] + " ");
}
System.out.println();
}
}연결리스트를 이용한 이진 트리 구성
class Node{
char data;
Node left;
Node right;
public Node(char data, Node left, Node right) {
this.data = data;
this.left = left;
this.right = right;
}
}
class BinaryTree{
Node head;
BinaryTree(){};
BinaryTree(char[] arr){
Node[] nodes = new Node[arr.length];
for (int i = 0; i < arr.length; i++) {
nodes[i] = new Node(arr[i], null, null);
}
for (int i = 0; i < arr.length; i++) {
int left = 2 * i + 1;
int right = 2 * i + 2;
if(left < arr.length){
nodes[i].left = nodes[left];
}
if(right < arr.length){
nodes[i].right = nodes[right];
}
}
this.head = nodes[0];
}
public void preOrder(Node node){
if(node == null){
return;
}
System.out.print(node.data + " ");
this.preOrder(node.left);
this.preOrder(node.right);
}
public void inOrder(Node node){
if(node == null){
return;
}
this.inOrder(node.left);
System.out.print(node.data + " ");
this.inOrder(node.right);
}
public void postOrder(Node node){
if(node == null){
return;
}
this.preOrder(node.left);
this.preOrder(node.right);
System.out.print(node.data + " ");
}
public void levelOrder(Node node){
Queue<Node> queue = new LinkedList<>();
queue.add(node);
while(!queue.isEmpty()){
Node cur = queue.poll();
System.out.println(cur.data + " ");
if(cur.left!= null){
queue.offer(cur.left);
}
if(cur.right != null){
queue.offer(cur.right);
}
}
}트리의 각 요소 가져오는 메서드 구현
package org.example;
// 연결리스트를 이용한 이진트리 구성
import java.util.LinkedList;
import java.util.Queue;
class Node{
char data;
Node left;
Node right;
Node parent;
public Node(char data, Node left, Node right, Node parent) {
this.data = data;
this.left = left;
this.right = right;
this.parent = parent;
}
}
class BinaryTree{
Node head;
BinaryTree(char[] arr){
Node[] nodes = new Node[arr.length];
for (int i = 0; i < arr.length; i++) {
nodes[i] = new Node(arr[i], null, null, null);
}
for(int i = 0; i < arr.length; i++){
int left = 2 * i + 1;
int right = 2 * i + 2;
if(left < arr.length){
nodes[i].left = nodes[left];
nodes[left].parent = nodes[i];
}
if(right < arr.length){
nodes[i].right = nodes[right];
nodes[right].parent = nodes[i];
}
}
this.head = nodes[0];
}
public Node searchNode(char data){
Queue<Node> queue = new LinkedList<>();
queue.add(this.head);
while(!queue.isEmpty()){
Node cur = queue.poll();
if(cur.data == data){
return cur;
}
if(cur.left != null){
queue.offer(cur.left);
}
if(cur.right != null){
queue.offer(cur.right);
}
}
return null;
}
public Integer checkSize(char data){
Node node = this.searchNode(data);
Queue<Node> queue = new LinkedList<>();
queue.add(node);
int size = 0;
while(!queue.isEmpty()){
Node cur = queue.poll();
if(cur.left != null){
queue.offer(cur.left);
size++;
}
if(cur.right != null){
queue.offer(cur.right);
size++;
}
}
return size + 1;
}
}
public class Main {
public static void main(String[] args) {
char[] arr = new char[10];
for(int i = 0; i < arr.length; i++){
arr[i] = (char)('A' + i);
}
BinaryTree bt = new BinaryTree(arr);
// Root node
System.out.println("ROOT : " + bt.head.data);
//B's Child node
Node B = bt.searchNode('B');
if(B.left != null){
System.out.println("B -> left child: " + B.left.data);
}
if(B.right != null){
System.out.println("B -> right child: " + B.right.data);
}
// F's parent node
Node F = bt.searchNode('F');
System.out.println("F -> parent : " + F.parent.data);
// Leaf node
System.out.print("Leaf node: ");
for (int i = 0; i < arr.length; i++) {
Node cur = bt.searchNode((char)('A' + i));
if(cur.left == null && cur.right == null){
System.out.print(cur.data + " ");
}
}
System.out.println();
// E's Depth (루트 부터 E까지 엣지를 몇번 거치는지)
Node E = bt.searchNode('E');
Node cur = E;
int cnt = 0;
while(cur.parent != null){
cur = cur.parent;
cnt++;
}
System.out.println("E depth : " + cnt);
// Level2 Node
System.out.print("Level2 node : ");
for (int i = 0; i < arr.length; i++) {
Node target = bt.searchNode((char)('A' + i));
cur = target;
cnt = 0;
while(cur.parent != null){
cur = cur.parent;
cnt++;
}
if(cnt == 2){
System.out.print(target.data + " ");
}
}
System.out.println();
//Height
int maxCnt = Integer.MIN_VALUE;
for (int i = 0; i < arr.length; i++) {
Node target = bt.searchNode((char)('A' + i));
cur = target;
cnt = 0;
while(cur.parent != null){
cur = cur.parent;
cnt++;
}
if(maxCnt < cnt){
maxCnt = cnt;
}
}
System.out.println("Height : " + maxCnt);
// B's Size
int size = bt.checkSize('B');
System.out.println("B size = " + size);
}
}연습문제
문제 1
// Practice1
// 종이 접기
// 종이를 반으로 접었을 때, 안으로 파인 부분은 0, 볼록 튀어나온 부분은 1이라고 하자.
// 종이를 접을 때는 오른쪽에서 왼쪽으로 접는다.
// 종이를 N번 접었을 때의 접힌 상태를 출력하는 문제를 작성하세요.
// 입출력 예시
// 입력: 1
// 출력: 0
// 입력: 2
// 출력: 0, 0, 1
// 입력: 3
// 출력: 0, 0, 1, 0, 0, 1, 1
public class Practice1 {
public static void solution(int n) {
int[] binaryTree = new int[(int)Math.pow(2,n)];
binaryTree[0] = 0;
for (int i = 0; i < (int)Math.pow(2, n-1) - 1; i++) {
binaryTree[i * 2 + 1] = 0;
binaryTree[i * 2 + 2] = 1;
}
inOrder(binaryTree, 0);
System.out.println();
}
public static void inOrder(int[] arr, int idx){
int left = 2 * idx + 1;
int right = 2 * idx + 2;
if(left < arr.length-1){
inOrder(arr,left);
}
System.out.print(arr[idx] + " ");
if(right < arr.length - 1){
inOrder(arr,right);
}
}
public static void main(String[] args) {
// Test code
solution(1);
solution(2);
solution(3);
}
}
문제 2
// Practice2
// 각각의 에지에 가중치가 있는 포화 이진 트리가 있다.
// 루트에서 각 리프까지의 경로 길이를 모두 같게 설정하고,
// 이 때, 모든 가중치들의 총합이 최소가 되도록 하는 프로그램을 작성하세요.
class BinaryTree{
int h;
int[] arr;
int result;
public BinaryTree(int h, int[] w){
this.h = h;
arr = new int[(int)Math.pow(2, h+1)];
result = 0;
for (int i = 2; i < (int)Math.pow(2, h+ 1); i++) {
arr[i] = w[i - 2];
}
}
public int dfs(int idx, int h){
if(this.h == h){
result += arr[idx];
return arr[idx];
}
int left = dfs(idx * 2, h + 1);
int right = dfs(idx * 2 + 1, h + 1);
result += arr[idx] + Math.abs(left-right);
return arr[idx] + Math.max(left,right);
}
}
public class Practice2 {
public static void solution(int h, int[] w) {
BinaryTree bt = new BinaryTree(h,w);
bt.dfs(1,0);
System.out.println(bt.result);
}
public static void main(String[] args) {
// Test code
int h = 2; // 트리 높이
int[] w = {2, 2, 2, 1, 1, 3}; // 트리에서 각각 에지의 가중치
solution(h, w);
System.out.println();
h = 3;
w = new int[]{1, 2, 1, 3, 2, 4, 1, 1, 1, 1, 1, 1, 1, 1};
solution(h, w);
}
}추가개념
트리는 노드와 엣지로 연결된 그래프의 특수한 형태
-> 즉 그래프의 표현으로도 tree를 표현할 수 있다
- 순환 구조(Cycle)을 가지지 않고, 1개의 루트 노드가 존재
- 루트 노드를 제외한 노드는 단 1개의 부모 노드를 가짐
- 트리의 부분 트리 역시 트리의 모든 특징을 가짐
트리에서 임의의 두 노드를 이어주는 경로는 유일
코딩테스트에서 트리에 관한 문제가 나올떈 크게 2가지
그래프로 푸는 트리
트리도 노드와 엣지가 있음(이를 인접리스트로 표현가능 -> DFS나 BFS 이용해서 푸는 문제)
이떄는 트리를 그냥 그래프처럼 인접리스트로 표현하고 탐색 알고리즘 이용트리만을 위한 문제
트리 중에서도 이진트리 & 세그먼트 트리(index Tree) & LCA(최소 공통 조상)
여기서 세그먼트랑 LCA는 좀 어려움(이중에선 세그먼트 트리 자주 나옴 : 이는 트리만을 위한 문제)
-> 이들은 1차원 배열로 트리를 표현
