파라메트릭 서치 (Parametric Search) 22.6.6

파라메트릭 서치란

최적화 문제(문제의 상황을 만족하는 특정 변수의 최솟값, 최댓값을 구하는 문제)를 결정 문제로 바꾸어 푸는 것

• 최적화 문제 : 상황을 만족하는 변수의 최솟값, 최댓값을 구하는 문제
• 결정 문제 : Yes, No 중 하나로 답할 수 있는 문제

문제를 풀어나가는 과정이 바이너리 서치(이분 탐색)와 매우 흡사하다. 파라메트릭 서치는 의외의 문제들에 적용돼서 최적화 문제들을 조금 더 쉽게 풀 수 있게 해준다.

파라메트릭 서치의 핵심은 결정 문제다. 해당값이 정답이 될 수 있는 값인지 아닌지를 쉽게 판단할 수 있어야(즉, 결정 문제를 쉽게 풀 수 있어야) 최적화 문제를 파라메트릭 서치로 풀 수 있다. 또한, 정답이 될 수 있는 값들이 연속적이어야 파라메트릭 서치를 이용할 수 있다.

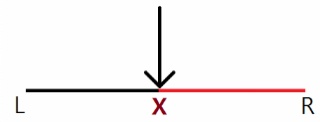
결정 문제를 정의했을 때, 쉽게 풀 수 있는 경우

• (최솟값을 구하는 경우) 최솟값이 x라면, x이상의 값에 대해서는 모두 조건을 만족
• (최댓값을 구하는 경우) 최댓값이 x라면, x이하의 값에 대해서는 모두 조건을 만족

https://www.acmicpc.net/problem/2343

백준 2343 문제

파라메트릭 서치를 사용하여 풀 수 있다.

N, M = map(int, input().split())
lessons = list(map(int, input().split()))

def f(n):
    sum = 0
    cnt = 1
    for lesson in lessons:
        if sum + lesson <= n:
            sum += lesson
        else:
            cnt += 1
            sum = lesson        
    return cnt

lo = max(lessons)
hi = sum(lessons)
mid = (lo + hi) // 2
ans = 0
while lo <= hi: 
    if f(mid) <= M: # 최솟값을 구하니 <=, f(mid)가 작다는건 블루레이 크기가 크다는것 
        ans = mid # 이분 탐색과 흡사하다
        hi = mid - 1
    else:
        lo = mid + 1
    mid = (lo + hi) // 2
print(ans)