
CPP Module 02
해당 과제를 진행하는데 있어 필요한 사전 지식들을 정리하였습니다.
1. Orthodox Canonical Form
Canonical Form이란 정해진 규칙을 정확히 따르며 개발하는 프로그래밍을 의미한다. 일종의 code convention이라고 볼 수 있다. 과제에서 요구하는 해당 형식은 다음 네 가지의 형태를 명시적으로 정의하여 선언하는 것을 가리킨다.
- 기본 생성자
- 복사 생성자
- 대입 연산자 오버로딩
- 소멸자
1-1. 기본 생성자
기본 생성자는 별도로 생성자를 구현하지 않을 시 사용되는 생성자이다. 매개변수는 없고 멤버 변수가 0, NULL 등으로 초기화 된다.
1-2. 복사 생성자
ClassName::ClassName(const ClassName& ref)
{ ... }복사 생성자란 같은 클래스의 다른 객체의 참조자(Reference)를 인자로 받아, 그 참조를 이용해 자신의 객체를 초기화하는 클래스 함수이다. 기존 값을 복사하여 전달해주므로 const로 받는다. 복사 생성자를 직접 명시하지 않은 경우 기본 복사 생성자가 자동으로 생성된다. 이러한 기본 복사 생성자는 얕은 복사가 수행되며, 만약 깊은 복사가 필요하다면 사용자가 직접 정의해야 한다.
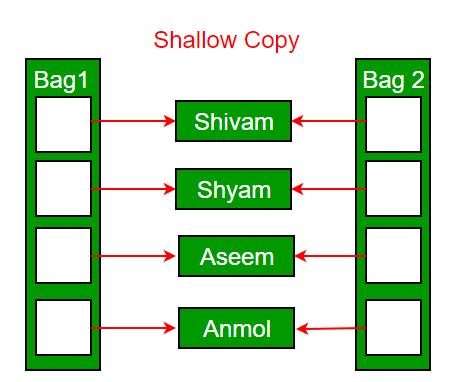
얕은 복사 (Shallow Copy)
얕은 복사는 원본 객체의 모든 클래스 변수의 데이터를 단순히 복사하여 객체를 생성한다. 그러므로 얕은 복사로 생성한 객체의 클래스 변수는 원본 객체와 동일한 메모리 위치를 참조한다. 따라서 원본 객체를 수정할 경우, 얕은 복사로 생성한 객체의 데이터도 변경되며, 그 반대의 경우도 성립한다.
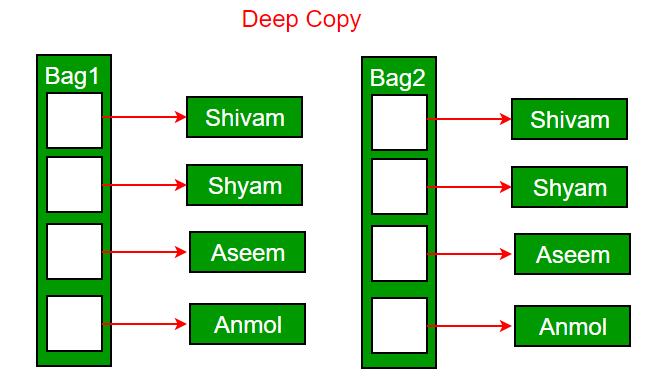
깊은 복사 (Deep Copy)
깊은 복사는 원본 객체의 모든 클래스 변수를 복사하기 위해 새로운 메모리 공간을 할당받아 원본 객체의 변수 값을 복사한다. 깊은 복사는 사용자가 복사 생성자를 명시적으로 정의해야 하고 그 과정에서 원본 객체에서 복사할 모든 클래스 변수에 대해 메모리 할당을 받아야 한다. 깊은 복사로 생성한 객체는 원본 객체와 다른 메모리 주소를 참조하고 있기 때문에 두 객체는 서로 영향을 주지 않는다.
1-3. 연산자 오버로딩
C++에서는 함수의 이름이 같아도 매개변수가 다르면 선언 및 정의가 가능하다. 오버로드(Overload)는 같은 이름을 가진 복수의 객체가 각각 다른 기능을 하도록 만드는 것이다.
객체끼리의 연산자(+, -, *, / 등)를 사용한 연산은 불가능하기 때문에 이를 가능하게 하려면 사용자가 연산자 오버로딩을 통해 연산자의 기존 기능을 재정의 해야한다.
오버로딩 방법은 다음과 같이 operator 키워드 뒤에 오버로딩할 연산자를 붙여주면 된다.
ClassName& ClassName::operator=(const ClassName& ref)
{ ... }1-4. 소멸자
소멸자는 객체의 수명이 다했을 때 객체를 제거하기 위한 목적으로 사용된다. 객체의 수명이 끝나면 컴파일러가 자동으로 소멸자 함수를 호출하게 되고 클래스명 앞에 ~기호를 붙여 정의할 수 있다.
2. 고정 소수점과 부동 소수점
2-1. 고정 소수점(Fixed point)
- 움직이지 않고 고정된 소수점
- 특정 숫자의 소수점 위치를 고정하는 방식
- ex)
123.45
컴퓨터 언어에서 데이터 타입은 항상 최대 길이가 고정되어 있다.

부호비트 : 양수면 0, 음수면 1
지수비트 : 정수부
가수비트 : 소수부
고정 소수점은 소수점이 붙어 있는 수를 2진수로 변환하는 과정에서, 10진수를 2진수로 바꾼 결과를 그대로 대입하는 방식이다. 예시로 7.625라는 실수를 2진수로 변환하면 111.101이 될 것이고 다음과 같은 형식이 될 것이다. (16비트 체계)
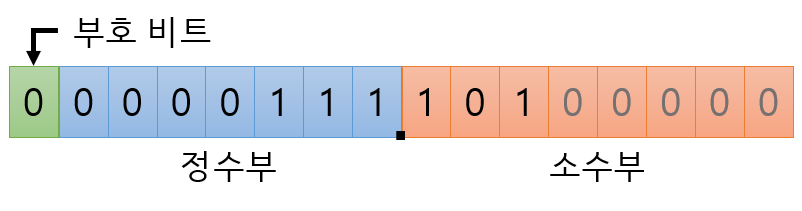
고정 소수점은 구현하기 편리하지만 범위의 정밀도가 낮아 소규모 시스템에서 간혹 쓰인다고 한다.
2-2. 부동 소수점(Floating point)
- 고정되지 않고 움직이는 소수점
float,double에서 사용하는 방식- ex)
1.2345 × 10^2=12.345 × 10
부동 소수점은 고정 소수점과 다르게 정규화(Normalization) 과정을 거친다. 이는 2진수로 변환 시 정수부에 1만 남겨두고 나머지를 소수부에 넣는 방식이다. (1.xxx × 2^n 형태로 변환)
부호비트는 양수면 0, 음수면 1을 저장한다.
지수부에는 2^n에서 n에 해당하는 지수를 넣게 되는데 그냥 넣는 것이 아니라 지수에 bias를 더한 값을 저장하게 된다. bias 계산법은 2^n-1 - 1이고 32비트 기준 127이다. (2^8-1 - 1 = 127)
가수부에는 소수값을 표현하고 나머지는 모두 0으로 채운다.
7.625를 부동 소수점으로 나타내면 다음과 같다.

7.625 → 111.101 → 1.11101 × 2^2
지수는 2이고 bias는 32비트 기준 127이므로 지수부에는 2 + 127 = 129가 변환되어 저장된다.
3. ex00 (My First Class in Orthodox Canonical Form)
ex00에서는 부동 소수점을 고정 소수점으로 변환하는데 필요한 기능을 대략적으로 살펴보았다. Canonical Form에 따라 기본 생성자, 복사 생성자, 연산자 오버로딩, 소멸자를 함수 호출 메시지와 함께 정의하였다. 또한 과제에서 요구하는 고정 소수점을 설정하는 함수와 고정 소수점을 반환하는 함수도 함수 호출 메시지와 함께 정의하였다.
복사 생성자 정의 부분에서 쓰인 객체간 =연산은 연산자 오버로딩된 =연산자이다.
4. ex01 (Towards a more useful fixed-point number class)
4-1. 정수 / 실수(부동 소수값) ↔ 고정 소수값
고정 소수값은 2진수 정수 혹은 부동 소수값의 소수 부분을 넣을 비트 수를 정해두고 표현하는 것이다. 과제에서 소수 부분을 넣을 비트(fractional bits)를 8로 정해주었기 때문에 32비트 체계에서는 앞의 24비트를 정수 부분, 뒤의 8비트를 소수 부분으로 표현한다.
1) 정수 → 고정 소수값
정수를 고정 소수값으로 표현하기 위해서는 앞으로 8비트만큼 << 비트 시프트 연산을 해서 8비트만큼의 빈 공간을 만들면 된다. 임의의 정수 n을 고정 소수 값으로 변환하려면 n << 8 해주면 된다. 그래야 마지막 8칸은 n.00000000와 같이 소수로 표현할 수 있기 때문이다.
n << 8orn * 256
2) 고정 소수값 → 정수
이 경우는 특정 값을 고정 소수점으로 변환한 것을 다시 원위치 시키면 된다. 즉 변환하고자 하는 값을 n이라고 한다면 n >> 8과 같이 변환하면 된다.
n >> 8orn / 256
3) 실수(부동 소수값) → 고정 소수값
정수와 동일하게 << 연산을 통해 Fractional Bits의 공간을 마련해주면 되지만 float나 double과 같은 부동 소수점의 경우 직접적으로 시프트 연산이 불가능하기 때문에 간접적으로 해야한다.
또한 현재 고정 소수점으로 저장할 클래스의 변수의 타입이 int형 이므로 일부 데이터가 누락될 수 있다. 그러므로 비교적 정확한 변환을 위해 허용 함수인 roundf를 통해 반올림을 진행할 필요가 있다.
임의의 실수 f를 고정 소수값으로 변환하려면roundf(f * (1 << 8))과 같이 변환하면 된다.
roundf(f * (1 << 8))orroundf(f * 256)
4) 고정 소수값 → 실수(부동 소수값)
이 경우는 실수를 고정 소수값으로 변환한 것을 반대로하면 된다. 다만 해당 과제에서 고정 소수값에서 실수로의 변환은 부동 소수점 → 고정 소수점 → 부동 소수점의 변환 방식을 의미한다.
그러므로 기존 클래스에 저장하고 있는 고정 소수점을 float로 강제 형변환하여 부동 소수점으로 변환한 뒤, 고정 소수점의 Fractional Bits를 표현하기 위해 << 연산한 값을 다시 되돌리면 된다.
즉 변환하고자 하는 값을 f이라고 한다면 (float)f / (1 << 8) 과 같이 변환하면 된다.
(float)f / (1 << 8)or(float)f / 256
4-2. << 연산자 오버로딩
cout는 ostream의 객체이다. 그러므로 클래스를 cout로 출력하고 싶다면, ostram 클래스의 operator<<를 재정의하면 된다. 과제에서 요구하는 operator<<은 클래스에 저장된 고정 소수점 값을 toFloat함수를 통해 부동 소수점으로 출력하는 것이다.
float Fixed::toFloat(void) const
{
return ((float)_value / (1 << _bits));
}
std::ostream& operator<<(std::ostream& os, const Fixed& obj)
{
os << obj.toFloat();
return os;
}
5. ex02 (Now we're talking)
Fixed 클래스에 다음의 연산자 및 함수들을 public 멤버 함수로 오버로드 해야한다.
- 비교 연산자 :
>,<,>=,<=,==,!= - 산술 연산자 :
+,-,*,/ - 증감 연산자 :
n++,++n,n--,--n(전위, 후위 모두) - min 함수 : 두 개의 고정 소수점 값에 대한 참조를 가져와 가장 작은 값에 대한 참조를 반환하는 정적 멤버 함수
- min 함수를 오버로드하여 가장 작은 상수 값에 대한 참조를 반환하는 min 함수
- max 함수 : 두 개의 고정 소수점 값에 대한 참조를 가져와 가장 큰 값에 대한 참조를 반환하는 정적 멤버 함수
- max 함수를 오버로드하여 가장 큰 상수 값에 대한 참조를 반환하는 min 함수
6. ex03 (BSP)
6-1. 과제 내용
기존 ex01에서 추가적으로 Canonical Form에 맞춰 Point라는 클래스를 정의한다. Point는 좌표를 의미하는 클래스이다.
또한 다음과 같은 함수를 정의한다.
bool bsq(Point const a, Point const b, Point const c, Point const point);bsq함수는 점 a, b, c를 꼭지점으로 하는 삼각형 내부에 점 point가 있는지 판단하는 함수이다. 점 point가 삼각형 내부에 있으면 true, 외부에 있으면 false를 반환한다.
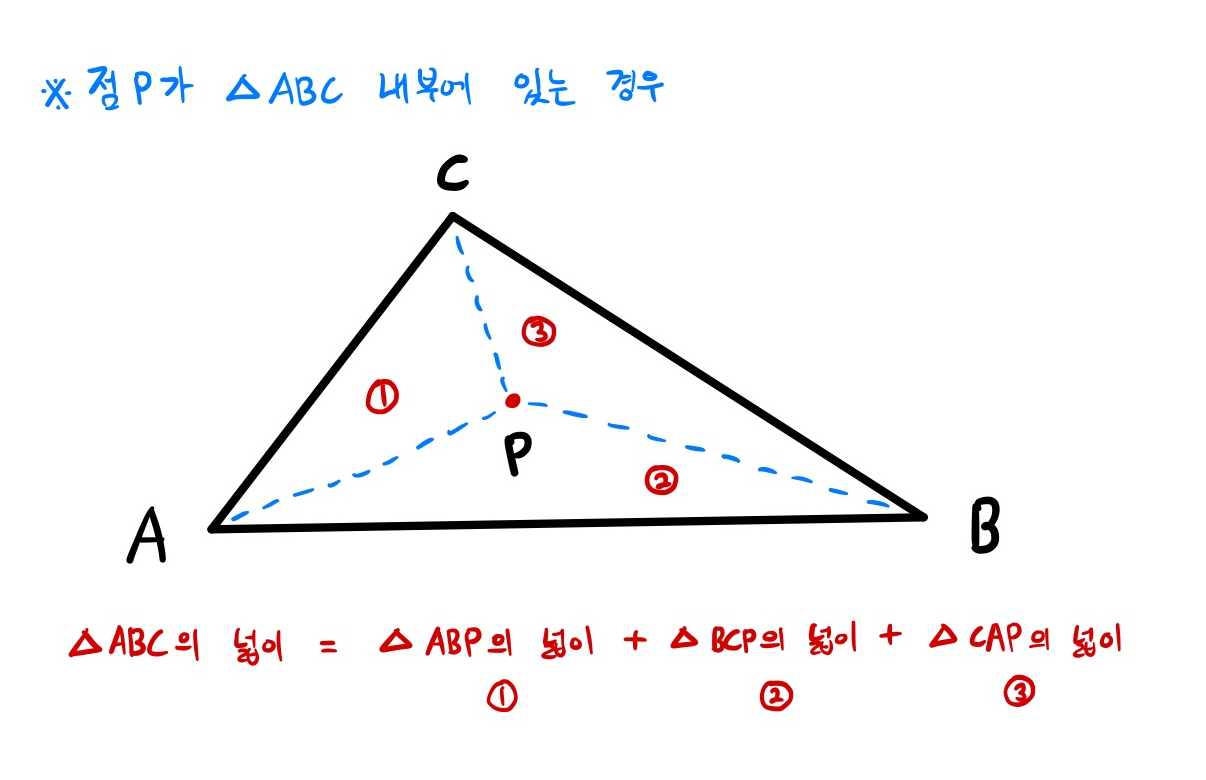
6-2. 주어진 점이 삼각형 내부에 있는지 확인하는 방법
▵ABC의 넓이 = ▵ABP의 넓이 + ▵BCP의 넓이 + ▵CAP의 넓이
위의 식이 참이면 점 P는 ▵ABC 내부에 있고, 거짓이면 점 P는 ▵ABC 외부에 있다.
6-3. 점 A(a, b), 점 B(c, d), 점 C(e, f)로 이루어진 ▵ABC의 넓이 구하는 공식
삼각형의 꼭지점 3개가 모두 주어졌을 때 삼각형의 넓이를 구하는 공식은 다음과 같다.
½ × |(ab + cf + eb) - (bc + de + af)|
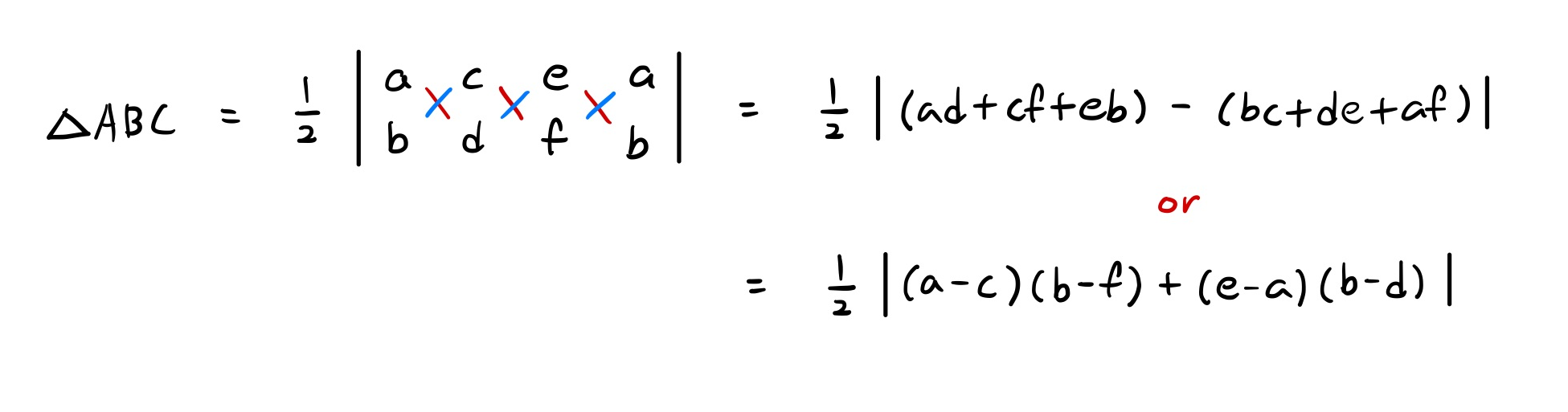
6-4. 증명
- 두 점의 거리공식을 활용하여 A와 B 사이의 거리를 계산한다. 이는 삼각형 ABC에서 밑변의 길이에 해당하는 값이다.
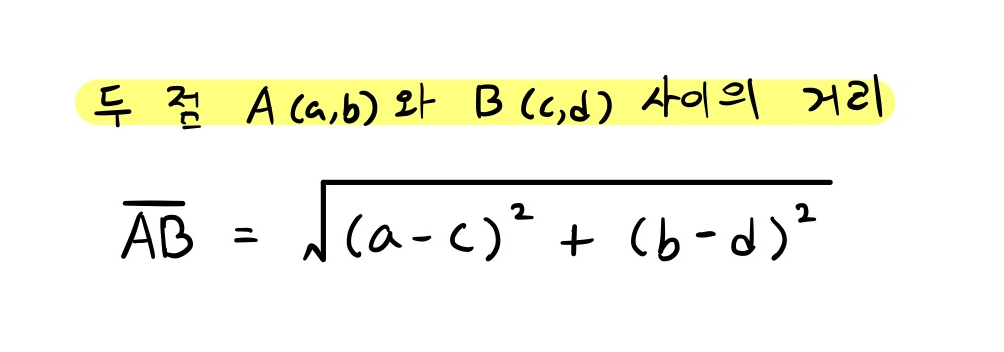
- C가 직선 AB에 내린 수선의 길이를 직선과 점 사이의 거리 공식을 활용하여 계산한다. 이는 삼각형 ABC에서 높이에 해당하는 값이다.
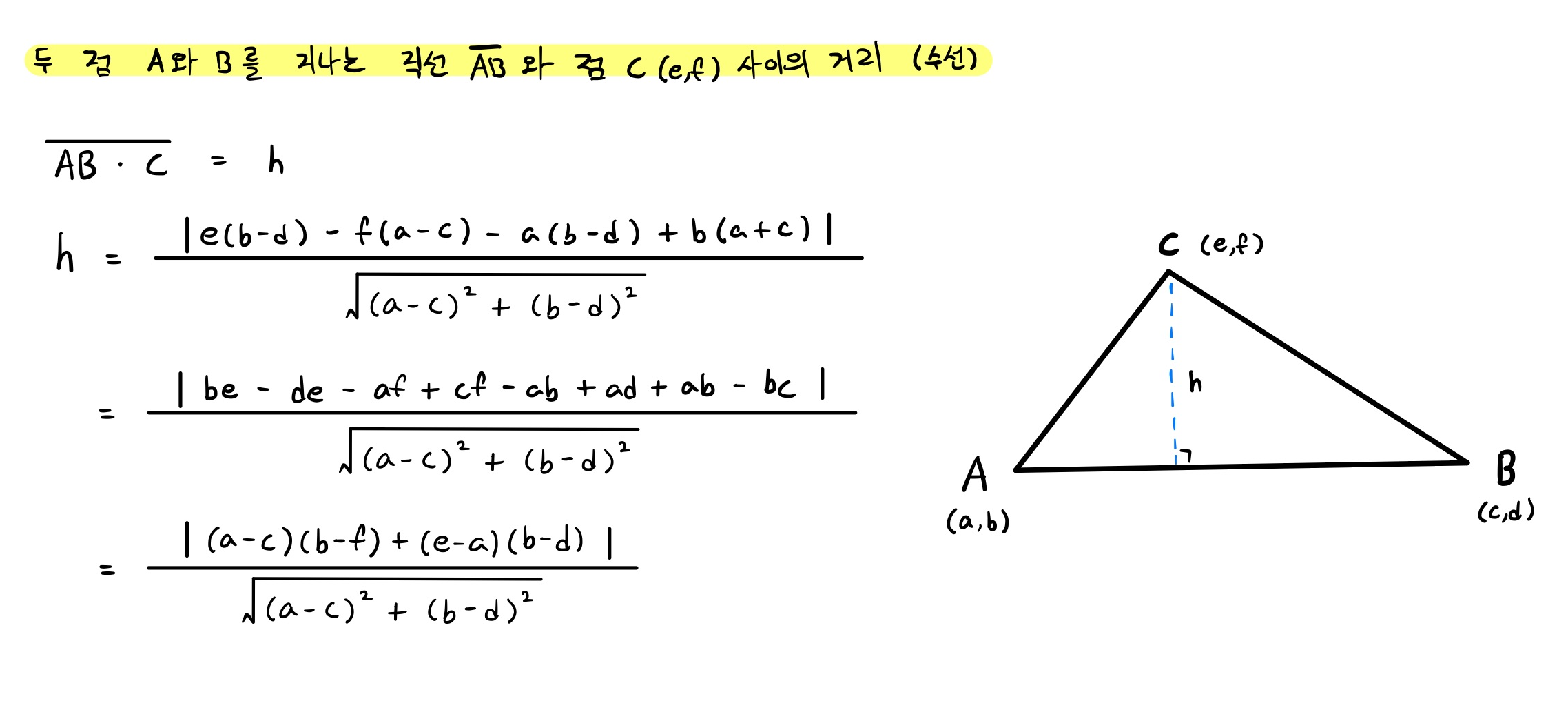
- 밑변의 길이와 높이를 알고 있으니 이제 넓이를 구하면 된다. 삼각형의 넓이는 밑변의 길이와 높이를 곱한 후 2로 나누는 식을 세운다.

참고
https://velog.io/@appti/CPP-Module-02-ex00
https://velog.io/@appti/CPP-Module-02-ex01
https://velog.io/@chaewonkang/42-Seoul-CPP-Module-02
https://velog.io/@seungju0000/cpp-module-02
https://velog.io/@hidaehyunlee/CPP-02-%EC%A0%95%EC%88%98%EB%B6%80%EB%8F%99%EC%86%8C%EC%88%98%EA%B0%92-%EA%B3%A0%EC%A0%95%EC%86%8C%EC%88%98%EA%B0%92-%EB%B3%80%ED%99%98
https://ko.wikipedia.org/wiki/%EC%A0%90%EA%B3%BC_%EC%A7%81%EC%84%A0_%EC%82%AC%EC%9D%B4%EC%9D%98_%EA%B1%B0%EB%A6%AC#cite_note-GEO-4
https://medium.com/@joongi1978/algorithm-3-%EC%84%B8-%EC%A0%90%EC%9D%84-%EC%95%8C-%EB%95%8C-%EC%82%BC%EA%B0%81%ED%98%95%EC%9D%98-%EB%84%93%EC%9D%B4%EB%A5%BC-%EA%B5%AC%ED%95%98%EB%8A%94-%EB%B0%A9%EB%B2%95-%EC%82%AC%EC%84%A0-%EC%8B%A0%EB%B0%9C%EB%81%88-%EA%B3%B5%EC%8B%9D-232ed0dc94d8
