챕터11. RISK NEUTRAL TREES AND DERIVATIVE PRICING

앞 서 이항구조가 가지고 있는 결함을 확인하였다

이러한 결함을 극복하기 위하여 risk neutral tree construction 전략을 구상하였다

그 중 하나는 위험중립확률을 고정시켜놓고 실제 채권의 가격과 일치시키는 노드를 설정하는 것이다

✏️ Risk Neutral Trees

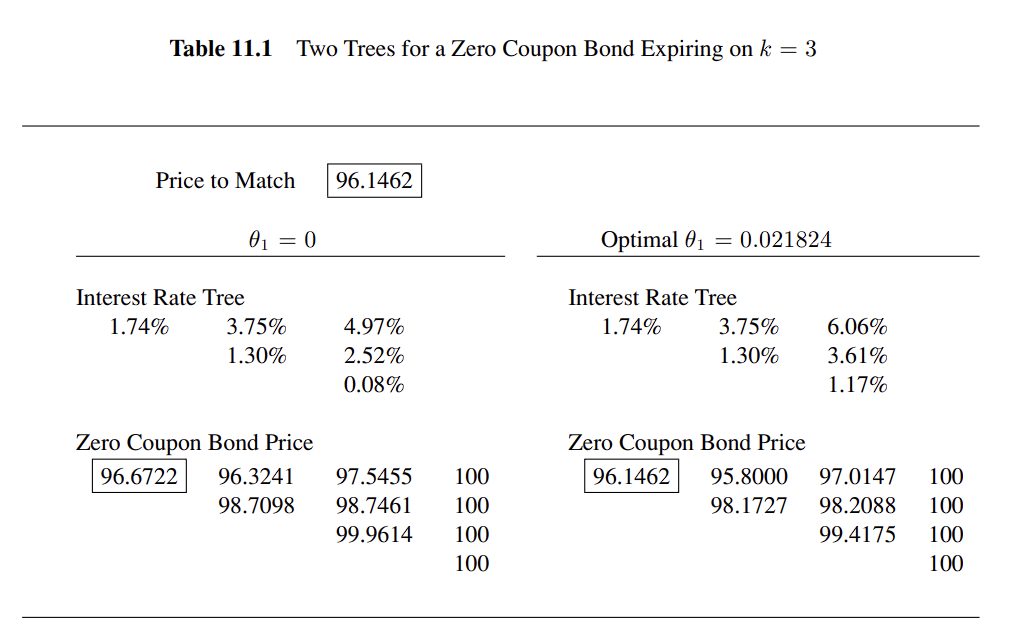
The Ho-Lee Model

이 모델은 이자율 기간 구조를 정확히 맞추는 간단한 모델 중 하나이다

$r_{i+1,j} = r_{i,j}+\theta_i\times \Delta + \sigma\times \sqrt \Delta$ with RN probability 1/2

$r_{i+1,j+1} = r_{i,j}+\theta_i\times \Delta - \sigma\times \sqrt \Delta$ with RN probability 1/2

위험 중립 확률은 모든 노드에서 같으며 각 노드에서 이자율 기간 구조를 맞춰주는 파라미터 $\theta$가 사용된다

simple BDT 모델

앞의 모델들은 음의 이자율이 나오는 결함이 있었다

BDT모델은 이를 극복하고자 나온 모델이다

Ho-Lee 모델과 유사하지만 이자율 $z_{i,g}$에 대하여 로그를 취한 값을 사용한다

$r_{i,j}=e^{z_{i,j}}$

따라서 로그 값은 음수가 나올 수 있지만 이를 다시 바꾸는 과정에서 양수가 나올 수 밖에 없다

이는 변동성을 조정하지 않는 간단한 형태의 BDT 모형이며

Ho-Lee 모델과의 차이는 로그를 취한다는 것이다 따라서 $\sigma$를 구할 때도 로그 데이터로 부터 얻어야 한다

두 모델의 비교

두 모형은 공통적으로 현재의 이자율 기간 구조를 맞추는 방식으로 진행된다

하지만 두 모형은 미래 금리의 내재 위험 중립 확률 분포에서 차이를 보인다

• Ho-Lee 모형은 음의 금리가 나올 가능성이 존재하며 높은 금리에 대하여 낮은 확률을 부여한다
  $\Delta$가 0에 다가갈수록 정규분포를 보인다
• simple BDT 모형은 1% 미만의 금리가 발생할 확률을 없애며 높은 금리에 더 높은 확률을 부여한다
  $\Delta$가 0에 다가갈수록 로그 정규분포를 보인다

이러한 차이는 채권 가격에 중요하지 않다

하지만 이 차이는 옵션같은 비대칭 payoff를 지닌 다른 상품에 있어서는 중요하다

simple BDT 모형이 가진 분포는 기대 payoff가 더 높다는 것을 의미하지만 동시에
더 높은 할인율을 적용해야 한다는 것을 의미하며 이 둘은 상쇄되어 BDT 모형이 더 낮은 가격을 도출한다

낮은 이자율에 대해서는 Ho-Lee, 높은 이자율에 대해서는 simple BDT가 좀 더 잘 설명한다

Risk Neutral Trees and Future Interest Rates

위험 중립 트리로부터 많은 정보를 얻고자 하는 유혹이 존재한다

예를 들어 1시점에 upcase와 downcase가 현재의 금리보다 높다면 금리가 무조건 올라갈 것이라 생각할 수 있다

하지만 이 트리는 오직 차익거래를 이용하여 금리 상품의 가격을 구하는 목적으로 고안된 것이다

또한 실세상에서는 위험 회피 성향을 고려해야하기 때문에
이러한 정보는 미래 금리에 대한 실제 금리와는 관련이 없다

Ho-Lee모형과 simple BDT모형에서 $\theta$를 통하여 위험 회피 성향을 고려하긴 하지만
확률분포에 따른 각각의 단점이 존재하며 이는 파생상품 가격에 영향을 미친다

✏️ Using Risk Neutral Trees

다양한 이자율 상품에 위험 중립 나무를 이용하여 가격을 구해보도록 하자

Intermediate Cash Flows

중간에 지급되는 cashflow가 있다면 어떻게 고려할 수 있을까?

$P_{i,j}=e^{r_{i,j}\times \Delta}\times({1\over 2}P_{i+1,j}+{1\over 2}P_{i+1,j+1}+CF(i+1))$

Caps and Floors

금리캡의 cashflow

$CF(T_i)=\Delta\times N\times max(r_n(T_i-\Delta)-r_K,0)$

n은 1년에 payment 횟수를 의미하고 $\Delta =1/n=T_i-T_{i-1}$이다

금리캡 상품 설명: https://barefoot911.tistory.com/20

금리플로어의 cashflow

$CF(T_i)=\Delta\times N\times max(r_K-r_n(T_i-\Delta),0)$

금리캡과 반대로 금리가 하락하는 것에 대한 보험이다

이 두 상품의 가격 결정에서 유의해야할 점은 시간차이다

금리가 결정되는 시점($i$)과 지급되는 시점($k$)의 시간차가 존재한다($k>i$ or $k=i+1$)

$CF_{i,j}(i+1) = \Delta\times N\times max(r_n(i,j)-r_k,0)$

$r_n(i,j)=n\times (e^{r_{i,j}\times \Delta} -1)$

$V_{i,j} = e^{-r_{i,j}\times \Delta}\times({1\over 2}V_{i+1,j}+{1\over 2}V_{i+1,j+1}+CF_{i,j}(i+1))$

Swaps

스왑은 앞의 장에서 확인하였듯이 할인율을 이용하여 쉽게 가치를 구할 수 있다

하지만, 시간이 흘러 지난 20년간 스왑의 가치에 의존하는 상품들의 수가 증감함에 따라
이자율 트리에 따른 역동적인 스왑 가치에 대한 이해가 요구되었다

바닐라 스왑의 cashflow

$CF(T_i)=\Delta \times N\times (r_n(T_i-\Delta)-c)$

Value tree

$CF_{i,j}(i+1)=\Delta \times N\times (r_n(i,j)-c)$

$V_{i,j}(k,c)=e^{-r_{i,j}\times \Delta}\times ({1\over 2}V_{i+1,j}(k,c)+{1\over 2}V_{i+1,j+1}(k,c)+CF_{i,j}(i+1))$

Swaptions

스왑션은 스왑을 기초자산으로 하여 스왑금리를 행사가로 정하여 계약을 맺는 옵션 상품이다

• receiver swaption은 고정금리를 받고 변동금리를 지급하는 스왑에 들어가는 옵션
• payer swaption은 고정금리를 지급하고 변동금리를 받는 스왑에 들어가는 옵션

스왑션은 보험역할을 하며 수의상환사채에 대한 헷지역할을 하기도 한다

그래서 우리는 어떻게 스왑션의 프리미엄을 계산할 수 있을까?

2년만기 스왑션이 존재하고 이에 대한 기초자산은 3년 스왑이라고 해보자
그렇다면 이 옵션이 행사되었을 때 스왑은 지금으로부터 5년후(행사 후 3년)에 종료될 것이다

먼저 스왑의 가치는 진입시 zero라는 것을 기억해야 한다
따라서 옵션의 만기시점에 가치는 0이다

$V_{i,j}(10,c_{i,j}(10))=0$

또 옵션의 만기 시점에 옵션이 행사되기 위해서는 그 시점의 스왑금리가 행사금리보다 커야한다

Payoff of swaption at time i=4 : $max(V_{4,j}(10,r_K),0)$

정리하자면

• 스왑 금리가 행사 금리와 같은 스왑의 가치를 계산한다

• 바로 위의 식을 이용하여 스왑션의 payoff를 계산한다

• 위험중립확률을 이용하여 뒤에서부터 앞으로 스왑션의 가치를 계산한다

✏️ 내재 변동성과 BDT모델

경험적 변동성은 과거의 실현된 변화에 따라 계산된 표준편차이다

이처럼 변동성이 주어지면 우리는 term structure에 완전히 fit하도록 트리를 계산한다

이때 경험적 변동성을 사용하여 구한 상품의 가치는 underprice되는 경우가 많다

그래서 시장에 존재하는 가격을 모델의 가격과 일치시키는 볼록성을 찾고자 하였고 이를 내재변동성이라 한다

먼저 시장의 가격에 따라 변동성이 선택되면 term structure는 알아서 fit된다

Ho-Lee모델의 경우 단기 caps에 대하여 overprice하고 장기 caps에 대하여 upderprice하는 반면
Simple BDT모델의 경우 항상 underprice한다는 것을 확인하였다

Flat and Forward 내재변동성

한 가지 큰 문제점은 변동성이 하나의 value가 아니라는 것이다

만기마다 다양한 변동성을 가지는데 이 때문에 변동성이 일정한 상황에서 상품 가격을 정확히 매길 수 있어도
만기가 달라지면 다시 계산해야한다는 것이다(같은 변동성으로 가격 측정 x)

이어서 implied flat volatility라는 개념이 나오는데
이는 미래의 모든 기간에 대하여 같은 변동성을 적용한다는 뜻이 아니다

단지 주어진 상품에 단 하나의 volatility값이 존재한다는 것을 의미한다
이때 주어진 상품은 만기와 행사가에 따라 하나의 상품으로 간주하여 둘 중 하나라도 다르면 다른 상품이다

Forward Volatility and BDT

각기 다른 만기와 행사가에 대하야 다양한 내재변동성이 필요하다는 것을 알아보았다

그렇다면 이러한 다양한 변동성은 복제를 불가능하게 만들 것인데 이 경우 차익거래 기회가 존재하는가?

모두 그러하지는 않다

대신 모든 무이표채와 caps를 정확히 일치시켜주는 모델을 배웠다는 것을 떠올려보자(BDT모델)

변동성에 시간 지표가 추가되면서 더 이상 recombining되지 않게 되었다

우리는 이자율이 상승했을 때와 하락했을 때의 차이를 알고 있기에 top interest rate를 구하고
밑에 부분을 구하는 식으로 트리를 간편하게 만들 수 있을 것이다 (the model still generates a recombining tree)

$z_{i,j+1} = z_{i,j}-2\times \sigma_i\times \sqrt{\Delta}$

$z_{i,j+1} = z_{i,0}-2\times(j+1)\times \sigma_i\times \sqrt{\Delta}$

이런 식의 트리를 구성한다면 i+1시점의 가격을 결정하는 i시점의 변동성을 알 수 있을 것이다
우리는 이를 forward volatility라고 하기로 했으며 이를 가중 평균한 값은 flat volatility라 할 수 있다

이러한 논리를 이용하여 다른 만기 상품에 대한 변동성이 서로 관련 있으니
앞의 replecate가 가능한 경우가 있다는 것이다

✏️ 선물 가격에 대한 위험 중립 트리

모든 시장 참여자가 위험 중립 성향을 가진다면 기대 수익은 얼마여야 할까?

선물 포지션에 진입할 때 비용을 지불하지 아니함으로 기대 수익은 zero여야 할 것이다

$E^*[F_{i+1}(k)-F_{ij}(k)]=0$

$F_{i,j}(k)={1\over 2}\times F_{i+1,j}(k)+{1\over 2}\times F_{i+1,j+1}(k)$

위의 식은 i+1시점의 가격을 통해 i시점의 가격을 얻는 backward를 가능하게 한다

만기에 선물가격은 해당 기초자산의 가치에 수렴한다는 것을 이용하여
final node의 가치를 구하여 역산한다

유로달러 선물

변동금리를 이용하여 $f_{k,j}(k)$를 구하고 이를 통하여 유로 달러 선물 가격을 추정한다

$F_{i,j}(k)=100-f_{k,j}(k)$

이렇게 내재 가치를 구하면 cap가격을 통하여 내재변동성을 구했던 것처럼
시장의 유로달러 가격과 일치하도록 하는 트리를 얻을 수 있을 것이다

3년만기 유로달러 선물이 유동적이기 때문에 실제로 트레이더들은 트리를 얻기 위하여 스왑대신 이를 이용한다

T-Note와 T-Bond 선물

국채 선물에 가치를 구하는 방법을 소개하기 전에 이 들의 가격에 영향을 미치는 요소를 알아보자

• Quality option

• Wild card option

• End-of-month option

위의 세가지 외에도 더 있지만 일단 품질 옵션에 대하여 고려해보자
국채의 특성상 T-bond의 경우 잔존 만기가 15년 이상남으면 적격자산이 된다
short포지션 보유자의 경우 이러한 점을 이용하여 cheapest-to-deliver을 하게 된다

Basis of Note $h=P_{k,j}^h-F_{k,j}(k)\times C^h$

즉 채권매입가격-청구가격(채권호가 - 선물가격*전환계수)을 최소화할 것이기 때문에
이를 만족하는 선물가격이 형성될 것이다

$F_{k,j}(k) = min{P_{k,j}^h\over C^h}$

이렇게 k시점 j상태에 선물 가격이 형성되면 이후에는 위험중립확률을 이용하여
나머지를 구할 수 있다

✏️ Implied Trees: Final remarks

이 장에서 설명한 방법들은 매우 강력한 도구이다

예를 들어 BDT는 모든 term structure에 fit하게 하는 모델이며

무이표채나 만기가 다른 cap을 이용하여 cap을 복제하는 방법들은 실로 매우 놀랍다

하지만 모든 것은 비용이 발생하며 여기서 비용은 overfitting이다

위 모델은 가격을 결정하길 원하는 상품의 수와 동일한 수의 자유도를 지니고 있다

즉, 파라미터에 대한 안정성이 부족하며 predicting power를 가지지 않을 것이다

그렇다면 우리는 이 모델을 왜 배웠으며 이를 가지고 어떤 것을 해야 하나라는 물음을 던질 수 있다

• 이 모델은 hedge ratio를 계산하기 용이하다.
  트레이더가 cap을 판매한다면 우리는 스왑을 기초자산으로 하는 포지션을 취하길 원한다

$Hedge\; ratio={c_{1,u}-c_{1,d}\over V_{1,u}-V_{1,d}}$

• 무이표채와 caps에 fit되었다면 스왑션 같은 다른 이자율 상품의 가격을 얻는데 이용할 수 있다