Matrix Decomposition

1. Properties

우선 eigen decomposition과 spectral decomposition을 다루기 앞서, 행렬 연산의 여러 속성들에 대해 간략히 요약해 보았다.

Inverse matrix에 관한 연산법칙

• $(A^{-1})^T = (A^T)^{-1}$
• if A is singular(rows are not independent), inverse matrix does not exist.

Determinent에 관한 연산법칙

• $|cA| = c^k |A|$, where k = 정방행렬 $A$의 차원
• $|AB| = |A||B|$
• $|A| = |A^T|$
• $|A^{-1}| = {1 \over |A|}$ if A is not singular
• A가 singular하다면, determinent of A는 0이 된다.
• A의 한 행이나 열이 영벡터 -> $|A| = 0$
• A의 두 행이나 열이 같은 벡터 -> $|A| = 0$

Trace sum

• $\mathbf{tr}(cA) = c \mathbf{tr} (A)$
• $\mathbf{tr}(AB) = \mathbf{tr}(BA)$
• $\mathbf{tr}(AA^T) = \sum_i\sum_j a_{i,j}^2$
• $\mathbf{tr}(B^{-1}AB) = \mathbf{tr}(A)$

2. Eigen Decomposition

$A \in \mathbb{R}^{k\times k}$일 때, 이 행렬에 대한 k 개의 고윳값과 k 개의 고유벡터들을 구함으로써, 행렬을 분해할 수 있고, 이 분해를 고유 분해(eigen decomposition) 라고 한다. 이 때, 고윳값들이 모두 unique하다면, 고유벡터들은 모두 독립(직교라는 보장은 없음)이며 노름(norm)이 1이 된다.

$P$ = eigen vector들을 column stack한 행렬(kxk dimesional)
$\Lambda$ = eigen value들을 대각 원소로 가지는 대각행렬(kxk dimensional)

이라 할 때, $A = P\Lambda P^{-1}$ 로 분해된다.

어떤 행렬 $A$에 대한 eigen value는 $\mathbf{det}(A-\lambda I)=0$ (characteristic equation)의 해를 풂으로써 구할 수 있고, 각 eigen value에 상응하는 eigen vector는 $Ax = \lambda x$를 만족하는 $x$를 찾음으로써 구할 수 있다.

이 때, eigen value중 0이 존재한다면, 이 행렬은 singular즉, 역행렬이 정의되지 않는다.

3. Spectral Decomposition

Spectral Decomposition은 분해의 대상이 되는 행렬 $A$가 대칭행렬이라는 점 외에는 eigen decomposition과 크게 다르지 않다.

$A$가 대칭행렬이면, eigen vector들이 독립일 뿐 아니라, 정규 직교(orthogonal)한다. 즉, 모든 eigen vector들의 pairwise dot product가 0이 된다.

정규 직교를 만족하기 때문에, eigen vector들을 column stack한 행렬(kxk dimensional) $P$는 $P^{-1} = P^{T}$를 만족한다. 따라서 기존의 행렬 A는 아래와 같이 분해된다.

$A = P\Lambda P^T = \sum_{i=1}^k \lambda_ia_ia_i^T$

통계학에서 많이 사용되는 공분산 행렬(Covariance matrix)은 대칭 행렬이자, 비음수 행렬(non-negative definite matrix)이다. 즉, 모든 고윳값이 0 이상이다.

4. Geometric Interpretation of Eigen value and vector

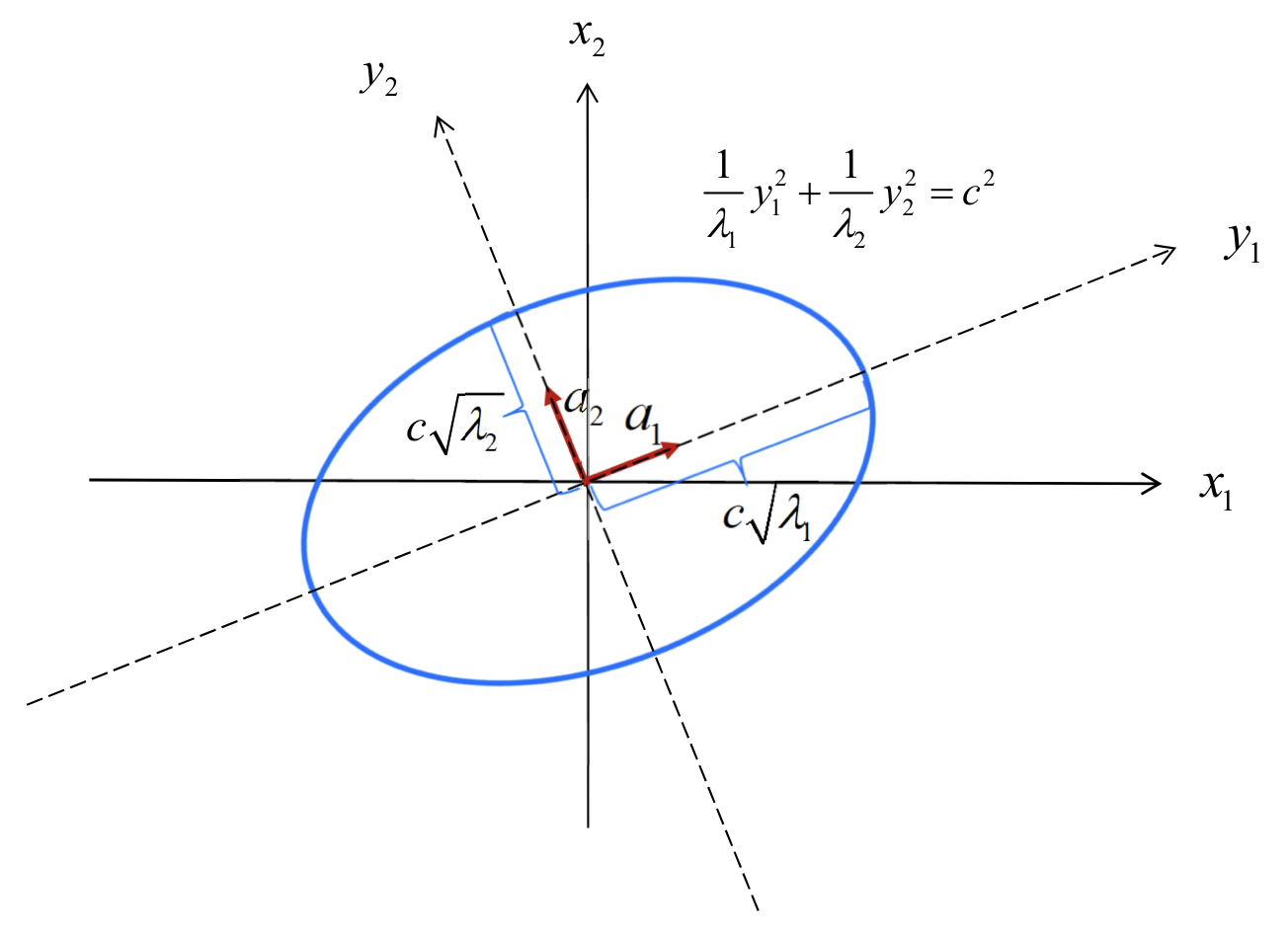
위 그림은 어떤 이변량 정규분포 상에서 같은 밀도를 가진 점들을 이어놓은 것이다. 수학적으로 이변량 정규분포 상에서 같은 밀도를 가진 점들을 이으면 타원이 정의된다. 차원을 확장하여, p-dimensional 다변량 정규분포 상에서 같은 밀도를 가진 점들은 p-dimensional ellipsoid(p차원 타원체)를 이룬다.

특정 p차원 다변량 분포에 대한 공분산 행렬은 대칭행렬이므로, 이 공분산 행렬에 대한 spectral decomposition을 생각해 볼 수 있다. 이렇게 얻어진 p개의 eigen vector는 각각 p-dimensional ellipsoid의 p개의 축을 의미하고, p개의 eigen value는 축 별 축의 길이를 의미한다.

이러한 인사이트는 다음 포스팅에서 설명할 principal component analysis(주성분 분석)과 밀접한 연관을 갖는다.