[논문리뷰] Node2Vec : Shallow embedding for node(2016)

Dong Jun·2022년 7월 12일

목록 보기

2/6

본 포스팅에서는 노드 임베딩을 학습하는 방법론을 소개한 2016년 논문, node2vec을 중점적으로 소개하고자 합니다. node2vec은 graph의 노드 임베딩을 직접 학습하는 shallow embedding approach를 따릅니다.

이 논문의 주요 포인트는,

1. 어떤 기준으로 노드 임베딩 간의 유사성을 정의하는가(dot product)
2. 어떤 방식으로 특정 노드의 neighborhood를 정의하는가(parameterized random walk)

라고 생각합니다.

Homophily & Structural Equivalence

본격적인 설명에 앞서, 그래프의 특성인 homophily와 structural equivalence에 대해 간략히 설명하겠습니다.

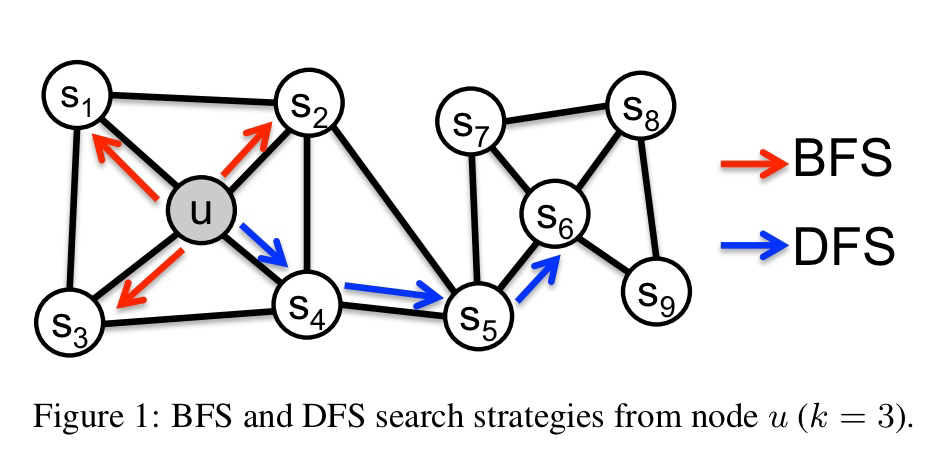homophily graph는 유사한 노드가 가까운 거리에 위치해 있습니다. 위 그래프가 homophily의 특성을 가졌다면, 노드 $u$ 와 노드 $s_1, s_2, s_3, s_4$ 가 유사하며, 이 그래프에서 특정 노드의 이웃을 정의할 때, 해당 노드 근처의 노드를 골라야 합니다.

sturctural equivalence 성질을 띠는 그래프는 다소 다릅니다. 이 그래프에서는 가까운 거리에 연결되어 있다고 해서 노드가 비슷한 성질을 갖는다고 할 수 없습니다. 거리가 멀더라도 구조적으로 비슷한 역할을 하는 노드가 유사한 노드입니다. 위 그래프가 structural equivalence 성질을 가진다면, 노드 $u$ 와 비슷한 노드는 $s_6$ 이 됩니다.

따라서 특정 노드를 기준으로 이웃 노드(성질이 비슷한 노드)를 고를 때, 그래프가 homophily의 성격을 띤다면 BFS의 방식으로 이웃 노드를 샘플링해야 하고, 그래프가 structural equivalence의 성격을 띤다면 DFS의 방식으로 이웃 노드를 샘플링 하는 것이 좋습니다.

Embedding Learning

모든 노드들의 집합을 $V$ 라고 하겠습니다. 이 때 임베딩 함수 $\mathcal{f}$ 는 각각의 노드를 $d$ 차원의 고정 길이 벡터로 맵핑합니다. 이 임베딩 함수 $f$ 는 $\mathbb{R}^{|V| \times d}$ 형태의 파라미터로 구성됩니다.

그리고, 특정 노드 $u$ 의 이웃 노드를 $\mathcal{N}_S(u)$ 라고 하겠습니다.

임베딩을 학습하는 기본적인 접근은 아래와 같습니다.
$\mathbf{argmax}_f \sum_{u \in V}\log Pr(\mathcal{N}_S(u) | f(u))$

즉, 어떤 노드 $u$ 의 임베딩(인코딩 된 표현)이 주어졌을 때, 이것을 디코딩(reconstruct)한 결과가 $u$ 의 이웃 노드일 확률을 최대화시키는 $f$ 를 찾는 것입니다. 임베딩 함수에 대한 학습을 maximum likelihood기반으로 수행하는 것이죠.

여기서 $Pr(\mathcal{N}_S(u) | f(u))$ 는 아래와 같이 개별 확률들의 곱으로 표현될 수 있습니다.(이웃 노드들 간의 독립을 전제)

$Pr(\mathcal{N}_S(u) | f(u)) = \prod_{n_i\in N_S(u)} Pr(n_i | f(u))$

그리고 본 논문에서는 $Pr (n_i | f(u))$ 을 dot product와 softmax로 아래와 같이 정의합니다.
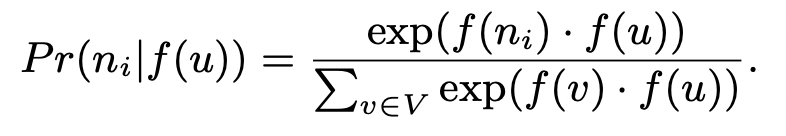하지만 이 표현에서 분모 부분을 계산하는 데 필요한 계산 비용이 매우 큽니다. 만약 노드가 수억개인 그래프라면, 하나의 노드에 대한 확률값을 계산하는 데에, 수억번의 덧셈 연산을 거쳐야 합니다. 따라서, 본 논문에서는 모든 node에 대해 분모 항을 계산하지 않고, 일정 개수의 negative node를 샘플링하는 방식으로 분모 항을 근사합니다. 따라서 최종적인 optimization objective는 아래와 같이 정의됩니다.

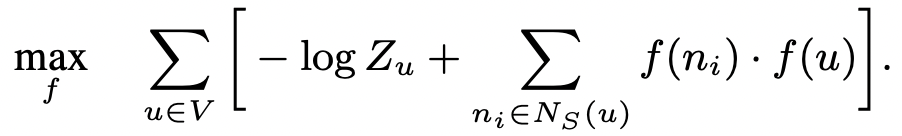
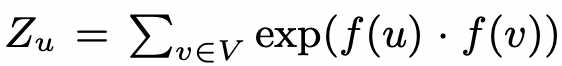( $Z_u$ 는 computationally expensive하므로, negative sampling을 통해 근사됨)

사실 이러한 프레임워크는 skip-gram과 같은 초기 언어 모델과 개념적으로 닮아 있습니다. skip-gram은 특정 단어가 주어졌을 때, 주변에 있는 단어의 발생 확률을 최대화 하는 방식으로 word embedding을 학습합니다.

어떤 노드가 주어졌을 때, 이웃 노드의 발생 확률을 최대화하는 방식으로 node embedding을 학습하는 Node2vec과 매우 유사합니다.

언어(문장)에서, 특정 단어의 이웃 단어는 말 그대로 위치적으로 이웃해 있는 주변 단어입니다.(물론 최근 NLP에서의 attention mechanism을 고려한다면 꼭 그렇지만도 않긴 합니다.)

하지만 그래프에서 특정 노드의 이웃 노드는 위치적으로 주변에 있는 노드 일수도 있지만 꼭 그렇지 않을 수도 있습니다(sturctural equivalence의 특성을 보이는 그래프의 경우). 따라서, optimization objective를 정의하는 것 만큼 중요한 것이 바로 특정 노드의 이웃 노드에 대한 정의입니다.

그리고 node2vec에서는, 이웃 노드에 대한 정의 방법으로 biased random walk를 사용합니다.

Defining Neighbor via Biased Random Walk

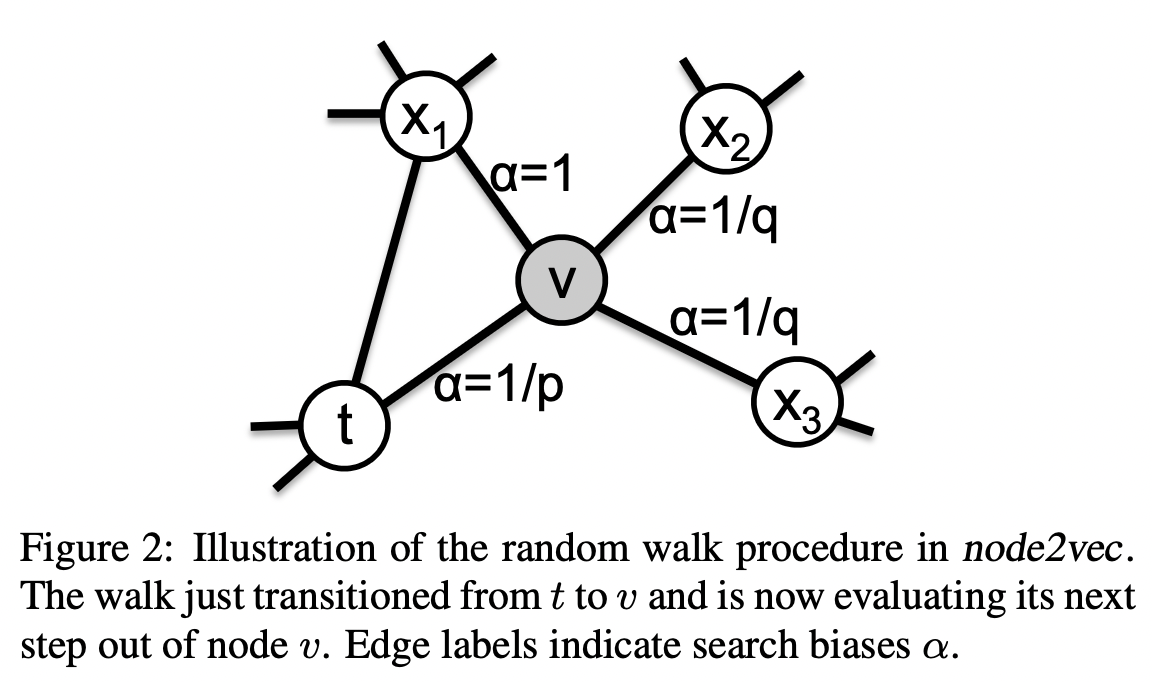
이웃 노드를 정의함에 있어 unbiased random walk를 사용할 수도 있지만, 그래프의 성질(homophily, structural equivalence)에 따라서 biased random walk를 사용하는 게 나을 수도 있습니다.

위 그림을 참고해 보겠습니다. 노드 $t$ 에서 random walk를 1회 수행하여 노드 $v$ 로 이동한 상황입니다. 여기서, $1/p$ 에 비례하는 확률로 이전 노드(노드 $t$ )로 돌아가고 $1/q$ 에 비례하는 확률로 아예 새로운 노드( $x_2$ or $x_3$ )를 탐색하며 1에 비례하는 확률로 이전 노드 t와의 거리가 1인 $x_1$ 으로 이동합니다.

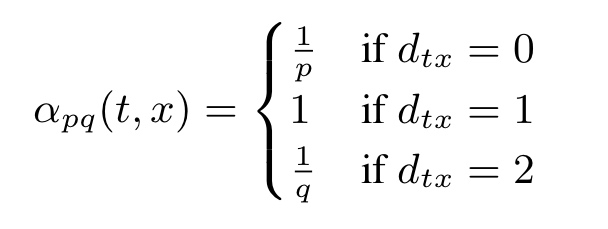
이 수식을 보면 됩니다. $\alpha_{pq}(t,x)$ 는 biased random walk를 위한 정규화되지 않은 확률(Unnormalized probability)이고, $d_{tx}$ 는 이전 노드 $t$ 와 이동 후의 노드 $x$ 간의 거리를 의미합니다. 원래 노드로 되돌아갈 경우( $d_{tx}=0)$ 이동 확률은 $1/p$ , 아예 새로운 노드로 이동할 경우( $d_{tx}=2$ ) 이동 확률은 $1/q$ , 기존 노드와 거리가 1인 노드로 이동할 경우( $d_{tx}=1)$ 이동 확률은 1에 비례합니다.