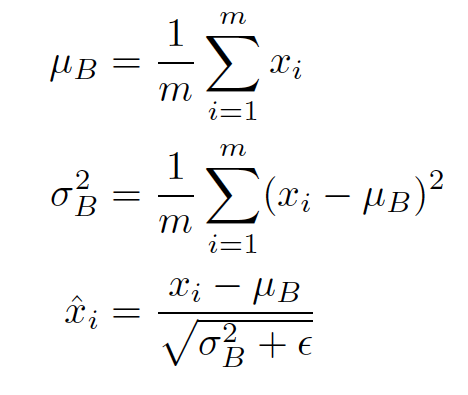Important Concepts in Optimization
(1) Generalization
일반화라는 것은 결국 학습데이터를 통해 모델이 충분히 학습한 후 테스트 데이터 등의 새로운 데이터를 모델이 접했을 때, 얼마나 모델이 원하는 결과를 내놓느냐를 의미한다.
(2) Underfitting and Overfitting
Underfitting(과소적합) 은 데이터에 비해 모델이 너무 간단하여 error를 줄이지 못하는 경우를 말하고, Overfitting(과대적합) 학습데이터에만 치중하여 모델이 복잡하게 학습되어 테스트 데이터에 대해 원하는 결과를 내놓지 못하는 경우를 말한다. 이러한 것들을 해결하기 위해 Dropout 등의 다양한 방법이 존재한다.
(3) Cross-validation(K-fold)
학습중인 모델의 성능을 평가하는 방법으로 Validation data를 사용하여 그 성능을 수치화하여 비교하고 하이퍼파라미터들을 조정하는 방법이 있다. 이 Validation data는 학습데이터나 테스트 데이터와는 절대 겹쳐서는 안되는 것이다. 하지만 만약 학습데이터 부터가 부족하다면 이중에 Validation data를 따로 확보하는 것은 매우 어렵다. 따라서 K-fold cross-validation 방법을 사용한다. 이는 학습데이터를 k개로 나눈후 k-1개는 학습에 사용되고 1개는 validation data로 사용하는 것이다. Validation data에 사용되는 1개의 데이터는 매 에폭마다 바뀌고 이렇게 총 K번 진행되며 각각의 학습오류와 검증오류의 평균을 통해 모델의 성능을 확인한다.
(4) Bias and Variance
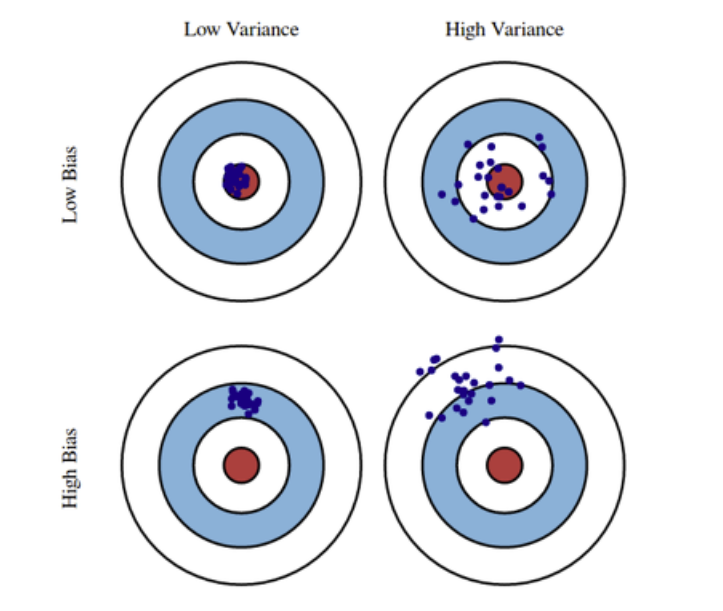
Variance는 데이터가 얼마나 일관되게 모여있는지를 의미하는 수치로 그 값이 낮아야 좋다. Bias는 데이터들이 True Target에서 얼마나 떨어져있는지를 나타내는 지표로 그 값이 낮을수록 True Target에 가깝다. Underfitting 모델의 경우 high bias 이며, Overfitting 모델의 경우 high variance 이다.
이 Variance와 Bias 사이에는 Trade-off 가 존재한다. 데이터 공간을 , , 라고 할때, cost의 기댓값은 다음과 같이 나타낼 수 있다.
식에서 알 수 있듯이, bias를 낮추면 variance가 올라가고 반대로 variance를 낮추면 bias가 올라가는 Trade-off 관계가 성립한다. 따라서 적절히 데이터를 Regularization하여 이를 조절하는 것이 중요하다.
(5) Bootstrapping
Bootstrapping은 학습데이터를 랜덤으로 섞어 여러 데이터셋을 만들고, 여러 모델에게 학습시킨 후 각 모델의 출력의 일관성을 테스트하는 것이다.
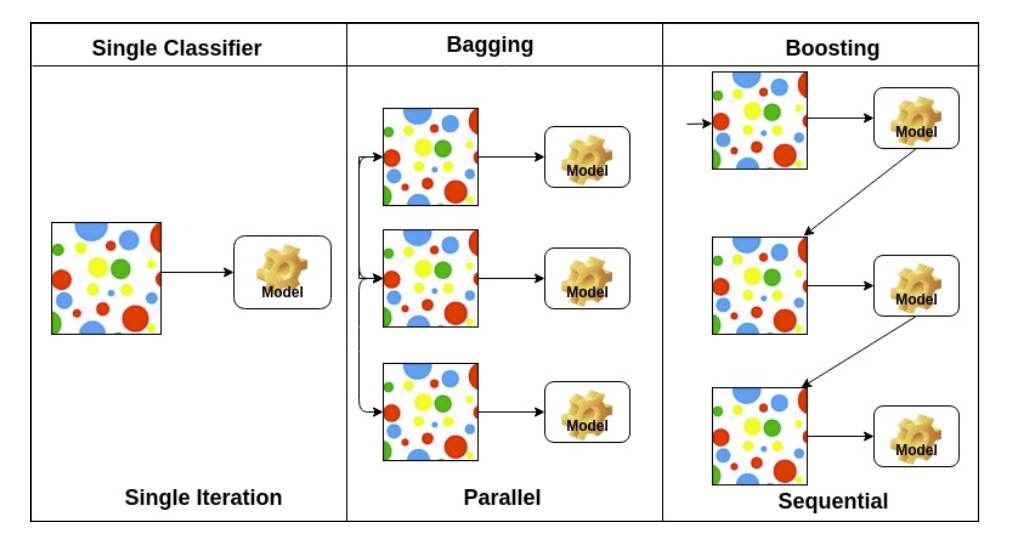
(6) Bagging vs Boosting
Bagging은 Bootstrapping aggregating의 약자로 앙상블학습과 같은 말인데, 여러 모델을 학습시킨 후 그 결과를 voting이나 averaging으로 활용하는 것이다.
Boosting은 반면 모델들을 병렬적으로 한번에 돌리는 것이 아니라 시퀀스로 연결해 이전의 약한 모델(weak learner)들에게서 나오는 실수들을 배우면서 학습을 정교하게 완성하는 기법이다.
2) Practical Gradient Descent Methods
시작하기 앞서 배치사이즈에 따른 성능에 대해 알아보고자 하는데, 배치를 너무 크게 쓴다면 Sharp minimizers로 converge할 수도 있다는 연구 결과가 있다. 그림을 보면서 얘기해보자.
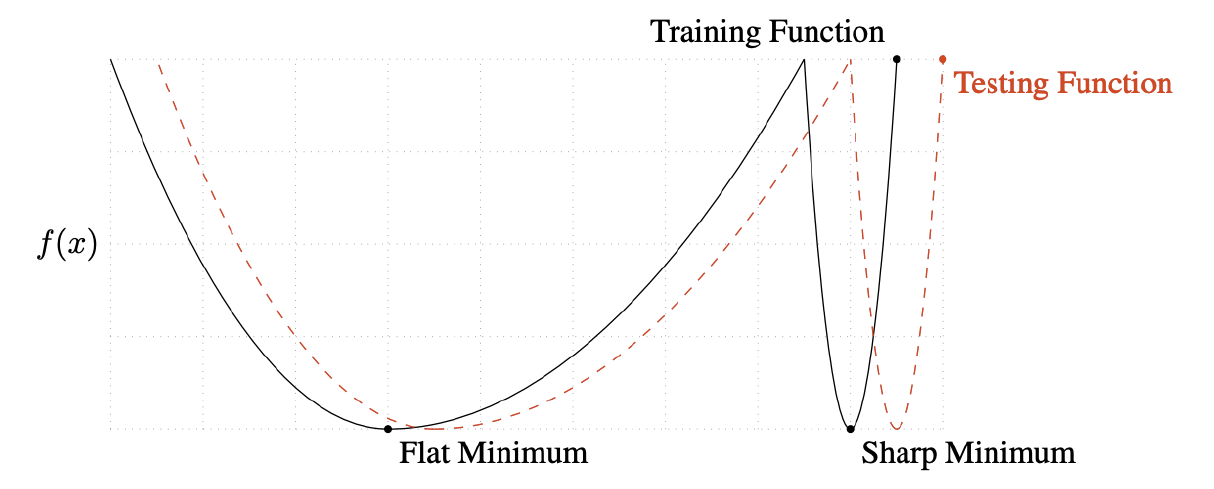
Sharp Minimum으로 converge된 모델이 Test function을 통해 근처의 x값이 주어질 경우 기존의 minimum값과 많이 다른 값을 받게 되어 결과가 좋지 않다. 반면 배치 사이즈를 적당히 작게 쓸 때는 Flat Minimum에 수렴하는데 이때는 x값이 조금 옆으로 가더라도 minimum값과 아주 조금 다르기 때문에 비교적 좋은 결과를 받을 수 있다.
(1) Gradient Descent
(2) Momentum
이전의 기울기에 대한 정보를 가속도(Momentum)처럼 새로운 그레디언트와 합쳐 갱신에 반영하는 기법
(3) Nesterov Accelerated Gradient
미리 모멘텀 항을 가중치 파라미터와 합쳐 구한 그레디언트를 사용, 더 빠른 converge가 가능
(4) Adagrad
자주 사용되는 파라미터에 대해서는 적게 갱신하고 덜 사용되는 파라미터들은 자주 갱신해준다. 는 그레디언트들의 제곱의 합이다.
(5) Adadelta
특이한 점은 learning rate가 없이 학습한다는 것이다. 와 는 EMA of gradient squares 로 지수이동평균을 의미한다.
(6) RMSprop
논문으로 따로 공개된 적이 없지만, 과거의 기울기는 서서히 잊고 새로운 기울기 정보를 좀 더 반영하기 위한 기법이다.
(7) Adam
Momentum기법과 RMSprop을 활용하여 가장 일반적이고 성능이 좋은 learning method이다.
3) Regularization
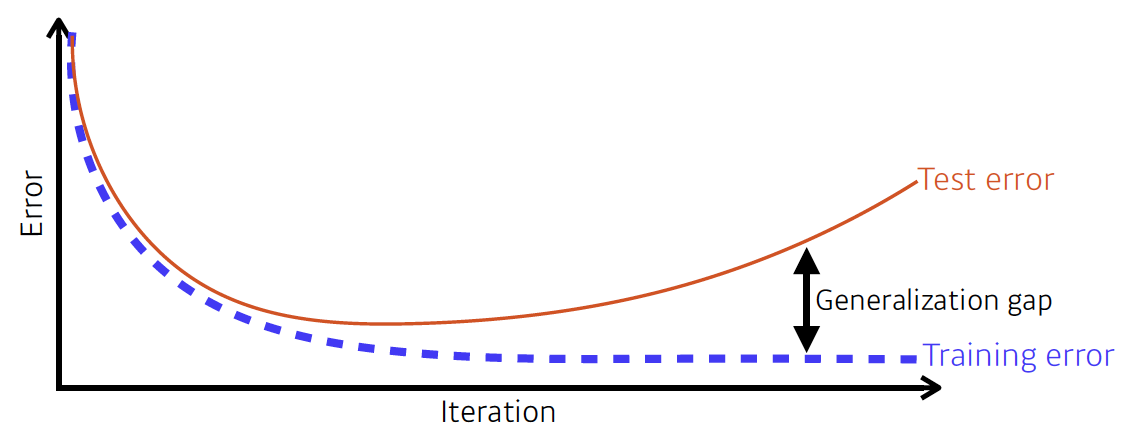
(1) Early stopping
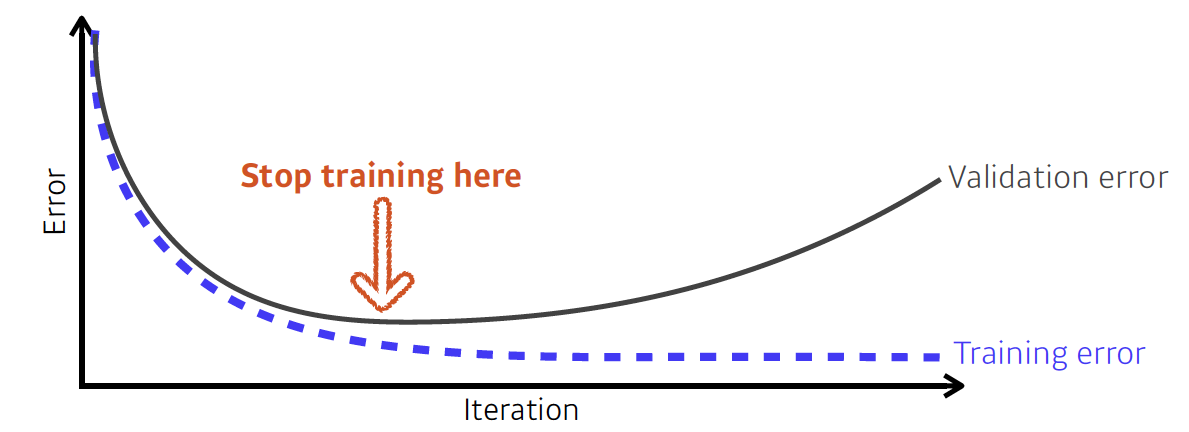
Validation 데이터셋으로 학습 중간에 모델의 성능을 확인하면서 만약 Validation error와 Training error의 차이가 일정 이상 벌어지면 학습을 멈추는 기법이다.
(2) Parameter Norm Penalty
total cost = loss + 로 페널티를 주는 것으로 function space에 smoothness를 더하는 기법이다.
(3) Data Augmentation
더 많은 데이터는 딥러닝에 있어서 무조건 좋다. 사진을 예로 들어서, 사진의 각도를 틀어보고 크기도 줄여보고 노이즈도 넣어서 데이터를 더 확보할 수 있다.
(4) Label Smoothing
Mix-up은 임의의 두 데이터의 input과 output 모두 잘 섞어서 decision boundary를 smoothness하게, 좀 더 잘 찾게 하기 위함이다. 반면 Cut-Mix는 한 데이터에서 일부를 잘라내고 다른 데이터를 갖다 붙인 뒤 그 결과 label을 각 데이터의 비율로 지정하는 기법이다. 목적은 Mix-up과 같다.
(5) Dropout
드롭아웃은 너무 유명한데, 순전파에서 layer간의 각 뉴런 연결에서 일부를 랜덤으로 끊어서 학습시키는 방법이다. 수학적으로 증명은 어렵지만 성능이 좋다고 알려져 있다.
(6) Batch Normalization
각 layer의 mean과 variance를 계산해 이에 맞게 파라미터들을 정규화(Normalization)하는 것이다. 성능에 대해 말들이 많다.