
이진분류
먼저, 이진분류에 대해서 알아보자. 이진분류는 간단하게 새로운 데이터가 주어졌을때, 사전 정의한 두가지 범주로 해당 데이터를 분류하는 것이다. train 데이터를 사용해 input과 target간 관계를 모델에 학습시킨다. 그 후, train 데이터에 포함되지 않는, 새로운 test 데이터를 사전에 정의된 두 범주 중 하나로 분류하는 모델을 구축하는 과정이다.
여기서, sigmoid 함수를 통해 모델의 output을 0~1 사이의 연속적인 값으로 매핑한다. 이때, 선형회귀때와 동일하게 MSE 손실함수를 정의할 수 있을까? 쉽지않다. 이진분류 문제에선 Binary Cross Entropy를 사용한다. Binary Cross Entropy는 이진 분류 모델의 predict 값과 target 값 간 차이를 측정하기 위해 사용되는 손실함수이다.
BCE (Binary Cross Entropy)
BCE는 시그모이드 함수에 의해 0~1사이로 계산된 연속적인 값 y와 target 과의 오차를 바탕으로 아래의 수식표현을 갖는다. 해당 수식표현이 도출된 과정을 살펴보자.
- 수식표현
일단 위의 수식을 토대로 생각해보면, target값이 1일 때, predict 값에 해당하는 가 1이면 와 이 모두 0이기 때문에, 오차가 0으로 계산되는 것을 알 수 있다. 마찬가지로, 0인 target에 대하여 0으로 predict하면 0으로 오차가 계산된다.
위의 수식을 유도하기 위해 조건부 확률과 로그 가능도 함수의 개념에 대해 살펴볼 필요가 있다.
조건부 확률
조건부 확률은 A가 발생한 상황을 전제하에, 다른 사건 B가 발생할 확률을 의미한다. 즉, 사건 B가 A의 발생에 의존하는 경우를 고려한다.
- 수식표현
간단한 예시로 다음 확률을 구해보자.
Q) 어느 고등학교에서 전체 학생의 60%가 안경을 썼고, 안경을 쓴 남학생이 전체 학생의 40%라고 한다. 이 학교의 학생 중에서 임의로 뽑은 한 명이 안경을 쓴 학생이었을 때, 그 학생이 남학생일 확률을 구하여라.
A)
안경을 쓴 경우 : A , 남학생인 경우 : B
안경을 쓴 확률 : , 안경을 쓴 남학생일 확률 :
안경을 쓴 학생이였을 때 (|A 전제), 학생이 남학생일 확률 :
최대 가능도 추정(Maxmimum Likelihood Estimation, MLE)
최대 가능도 추정은 주어진 데이터셋에 대해 모수를 측정하는 방법론이다. 데이터를 잘 설명하는 모수를 찾기 위해 가능도 함수를 최대화 하는 과정이다. MLE는 데이터의 분포에 따라 모수의 값을 추정하는 과정 전체를 가리킨다. 이때의 구체적인 모수값은 최대 가능도 추정치 라고한다.
- 최대 가능도 추정
모수를 추정하는 이유는 모델이 주어진 데이터를 가장 잘 설명하도록 하기 위함이다. 추정된 모수로 모델을 해석 및 평가할 수 있다.
- 최대 가능도 추정
가능도는 주어진 데이터가 모수 값 하에서 관찰될 확률이다. 쉽게 관측한 값이 어떤 확률분포로부터 나왔는지에 대한 확률이다. 확률과 고정되는 요소가 정반대이다. 관측치가 가정한 확률분포에 따라 특정 모수 값으로 설명될 가능도를 최대화 하는 방법으로 모수를 추정한다.
📌모수 : 모집단을 조사하여 얻을 수 있는 통계적인 특성치를 모수(Population Parameter)라고 하며 모집단 분포의 특성을 규정짓는 척도이다. 쉽게 확률분포의 파라미터라고 생각하면 된다.
확률과 가능도의 차이
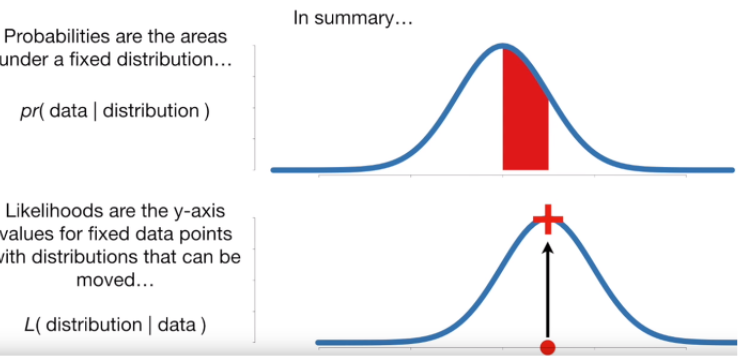
위의 그림은 확률과 가능도의 차이를 보여주는 그림이다. 먼저 확률은 고정된 확률분포 아래에서 데이터가 나올 가능성이다. 반대로, 가능도는 고정된 데이터 포인트에 대해 분포가 변할 수 있을 때의 가능성이다.
최대 가능도 추정이란, 각 관측값 X에 대한 총 가능도 ( 모든 가능도의 곱 )가 최대가 되게 하는 확률분포를 찾는 것이다.
베르누이 분포(독립시행)에 대해 확률분포 모수가 이고, n개의 관측데이터에 대한 가능도 함수는 아래와 같다.
위의 가능도 함수를 가장 크게 하는 파라미터 를 추정하는 것을 최대 가능도 추정이라고 한다.
가능도 함수를 최대화 하는 는 log 가능도 함수도 최대화 하기 때문에, log 가능도 함수를 사용하고, argmin으로 변환하며 음수 -1을 곱해준다.
위의 수식을 전개하면 아래와 같다.
최종 수식이 Binary Cross Entropy 형태임을 알 수 있다.
Reference
[출처] 조건부확률문제풀이(1-10번)|작성자 Spring
https://ahnjg.tistory.com/55
https://curt-park.github.io/2018-09-19/loss-cross-entropy/
