
Sigmoid for Binary Classification
linear regression의 값을 확률로 매핑 시켜주는 sigmoid 함수에 대해서 알아보자. 먼저, 그래프는 아래와 같다.
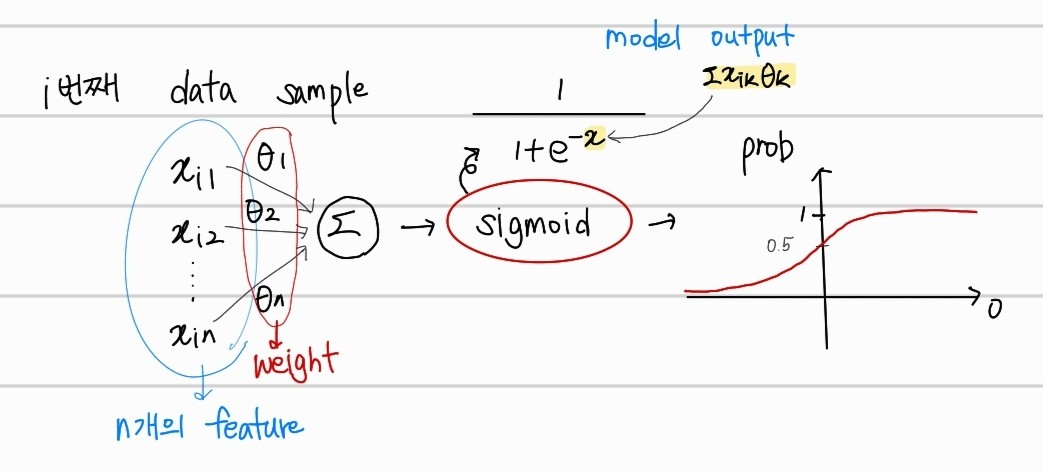
위의 그래프에서 x축은 linear regression의 결과 값(Output), y축은 그에 맞는 확률값(prob)을 의미한다. linear regression을 통한 예측값이 0보다 크면 1과 가까운 확률을, 0보다 작으면 0에 가까운 확률을 매핑해서 보여주는 함수이다.
수식은 아래와 같다.
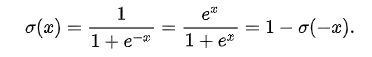
이제 이 수식이 어떻게 등장한 건지 알아보자.
Odds
먼저 sigmoid에 대한 증명을 위해서는 Odds(승산) 에 대해 알아야한다. 이는 확률의 다른 표현 방법으로, "일어나지 않을 확률 대비 일어날 확률" 을 의미한다. Odds가 클 수록, 당연히 일어날 확률이 커지는 것이다.
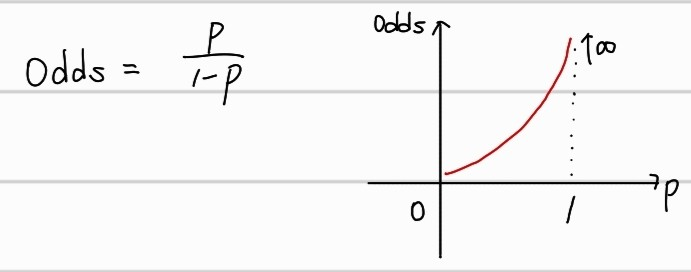
예를들어, 어떤 것이 일어날 확률을 0.8, 일어나지 않을 확률을 0.2라 했을 때, Odds값은 4가 된다.
Logit
logit은 Odds에 자연로그를 씌운 것이다. 수식과 그래프는 아래와 같다.
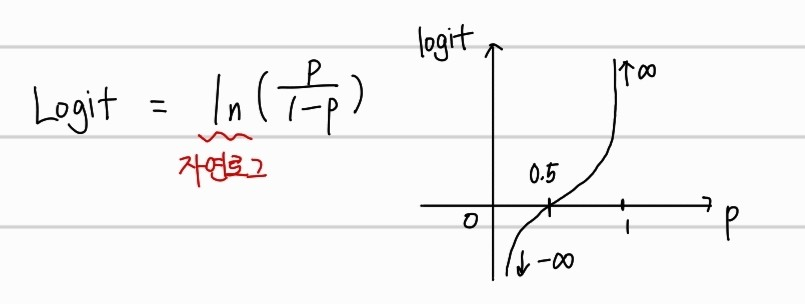
0에 가까운 확률이면 음의 무한대, 1에 가까운 확률이면 양의 무한대에 가까워지는 값을 가지게 된다. Logit 함수를 통해서 확률 값을 linear regression의 출력 범위인 실수 값으로 매핑할 수 있다.
Sigmoid (Logistic Regression)
위의 logit을 사용하여 linear regression의 결과를 확률로 매핑할 수 있게 해준다.

증명은 위와 같다. predict value는 음의 무한대에서 양의 무한대의 값이 나오는 Logit과 같다고 할 수 있다. 또한, 이를 확률 p에 대해서 정리하면 sigmoid 함수가 나오게 된다.
Sigmoid함수를 쓰는 이유는, linear regression의 결과값을 0과 1사이의 확률값으로 매핑하기 위해서이다. 이를 위해서, regression을 다른 표현 방법인 Logit으로 표현한 것이고, p에 대해 정리한 것을 통해 sigmoid 함수를 도출해 낼 수 있는 것이다. 그리고 이를 Logistic Regression이라고 한다. Odds, Logit, Sigmoid를 간단히 정리하면 아래와 같다.
- Odds : 사건이 발생한 확률을 발생안한 확률로 나눈 값으로, 사건 발생 가능성을 표현하는 방법이다.
- Logit : Odds의 자연로그를 취한 값으로 확률 값을 무한한 범위의 실수로 표현한다.
- Sigmoid : Logit 함수를 역함수로 사용해 linear regresion의 출력 값을 확률로 변환한다.
