DQN <2> 슬롯머신과 강화학습 그리고 Q

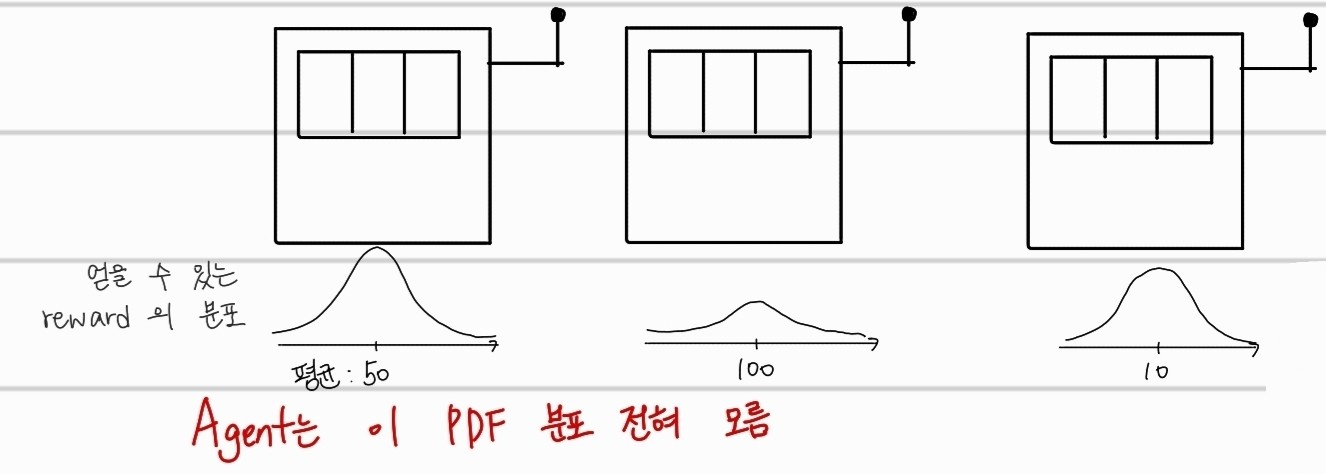
본격적으로 강화학습에 대해서 자세하게 들어가기전 한 가지 상황을 생각해보자. 위의 그림은 놀랍게도 슬롯머신을 그린 것이다. 각 슬롯머신은 정해져있는 돈이 아닌 확률분포에 따른 돈을 주게 된다. 한번에 하나의 슬롯머신을 선택할 수 있다면, 어떤 슬롯머신을 선택해야 더 많은 돈을 얻을 수 있을까?

맞다. 강화학습에서 reward에 따라서 행동을 선택해야하기 때문에, 그 기준을 잡는게 굉장히 중요하다. 이에 대해서 한번 수학적으로 공부해보자.

우선, 이때 각 슬롯머신이 주는 reward의 값은 처음에 알 길이 없으니 직접 추정해야한다. 일단 각 확률분포를 따를 때 reward를 평균으로 표현하자.

$q_*(a)=E[R_t|A_t=a]$ (확률분포의 평균값)
$Q_t(a)$ (t일때 a라는 action을 수행했을때 얻을 수 있는 가치)

Agent는 실제로 어떤 슬롯머신의 평균이 높은지, 슬롯머신이 주는 돈에 대한 확률분포는 무엇인지 등등을 알 방법이 없다. 따라서, action을 해가며 이를 학습해나가야한다. 이때, Agent는 당연히 reward를 많이 주는 슬롯머신을 선택해서 돌려야한다. 하지만, 무조건 reward를 많이 주는 슬롯머신만 고르면 안된다.

reward를 많이 주던 슬롯머신이 처음에만 운좋게 잭팟이 터진 케이스일 수 있기 때문이다. 때에 따라 아무리 reward가 높게 추측된 슬롯머신이 있더라도 한번쯤은 random하게 슬롯머신을 선택해서 돌려보는 경우도 필요하다.

이렇게 action을 선택함에 있어서, reward가 가장 큰 값을 선택하는 것과, 랜덤하게 다른 action을 선택해보는 것을 각각 Exploitation과 Exploration이라고 한다.

• exploitation : reward가 높은 action을 선택
• exploration : reward와 상관없이 random한 값을 선택

---

Epsilon-greedy method

$A_t=argmax_aQ_t(a)$ (greedy action)

위의 $A_t$는 reward(Q값)을 제일 최대로 얻을 수 있는 action이다. epsilon greedy method는 아주 작은 확률로 greedy action이 아닌 다른 action을 수행하는 경우를 만드는 방법이다. 식은 의외로 간단하다.

$\epsilon(explore)+(1-\epsilon)(exploit)$

충분히 많은 episode가 진행됐으면, 그에 맞게 직접 관찰하게 된 것을 바탕으로 각 슬롯머신의 reward 확률분포를 어느정도 아는 상태가 된 것이기 때문에, 더 이상의 exploration은 불필요해진다. 따라서 epsilon-greedy method는 위의 $\epsilon$값을 에피소드가 진행되는 거에 따라 점점 감소되게끔 진행한다.

---

action value의 예측을 위한 일반화

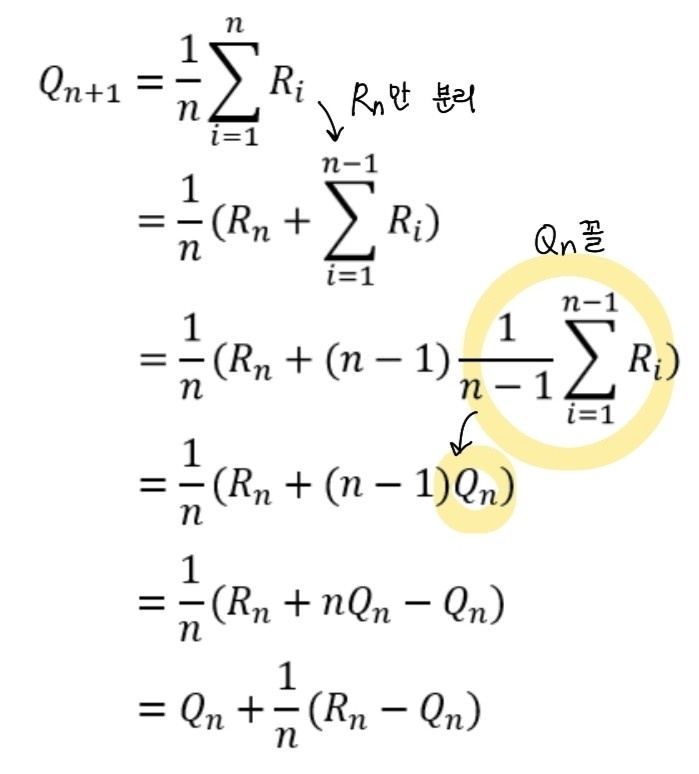$Q_{n+1}$은 a라는 action을 한 뒤의 next state에서 바라본, 다음 action a'에 대해 얻을 수 있는 action value이다. 이 값을 예측하는 과정이다. 우선, n번까지 action을 수행했다고 가정하자. 그것을 토대로 평균을 어떻게 계산할 것인지 예측하는 것이다. 최초의 식 $\frac 1 n \Sigma_{i=1}^nR_i$ 는 n번까지 수행한 reward의 평균을 의미한다. 여기서 마지막으로 받았던 reward를 제외한다. 그 뒤에 $\Sigma_{i=1}^{n-1}R_i$ 에 n-1씩 나누고 곱해주면, 두번째 항을 $Q_n$으로 나타낼 수 있다. 이로써, $Q_{n+1}$에 대한 식을 $Q_n$을 가지고도 작성할 수 있는 것이다.

$R_n$은 여기서 reward에 해당하는 값으로 예측하고 싶은값으로 여겨, target으로 생각한다. 따라서 아래와 같은 식이 되는 것이다.

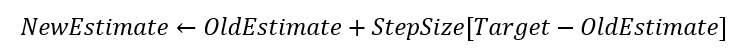
reward와 관련된 PDF는 정해져있지않고, 변하기 마련이다(non-stationary). 예를 들어, 슬롯머신에서도 사실 처음에 예상했던 PDF가 그대로 가지 않고, 어느정도 얻을 수 있는 기대수익이 변경될 것을 예측할 수 있다. 이를 해결하기 위해서 $\frac 1 n$이 아닌 상수 alpha값을 사용한다.

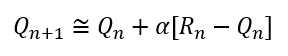
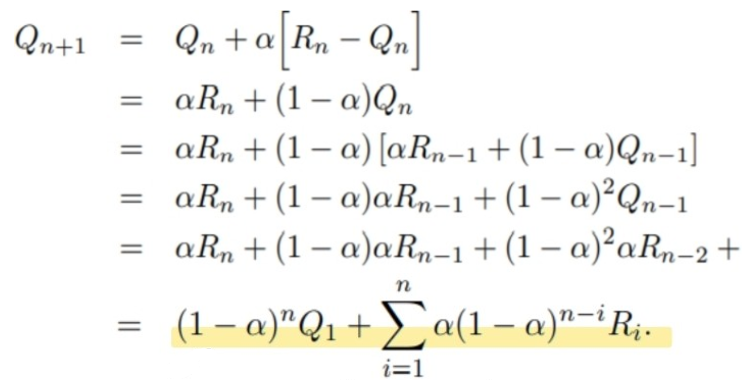
앞쪽의 episode에서 추정한 Q값과 뒤쪽의 episode에서 추정한 Q값이 완전히 다르게 되고, 오히려 이렇게 수렴하지않고 계속 달라야 변화하는 환경에 pdf가 변하는 환경에 잘 따라갈 수 있다.
이렇게 해서, action value $Q_{n+1}$의 일반적인 형태를 $Q_n+\alpha[R_n-Q_n]$으로 정의하게 된다.