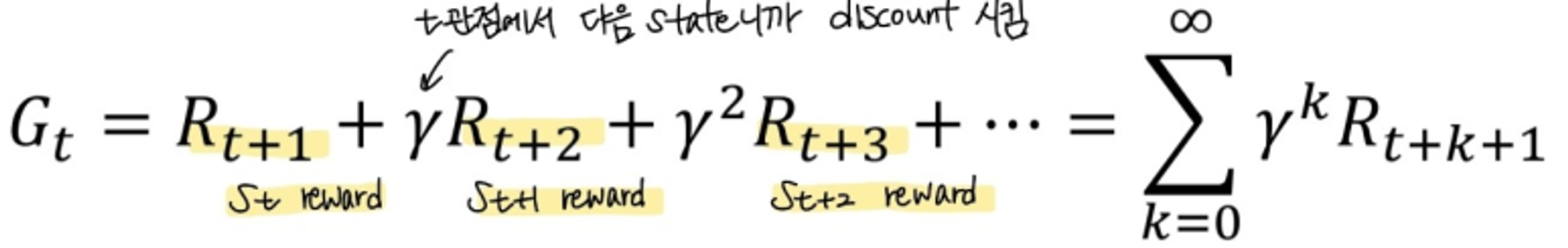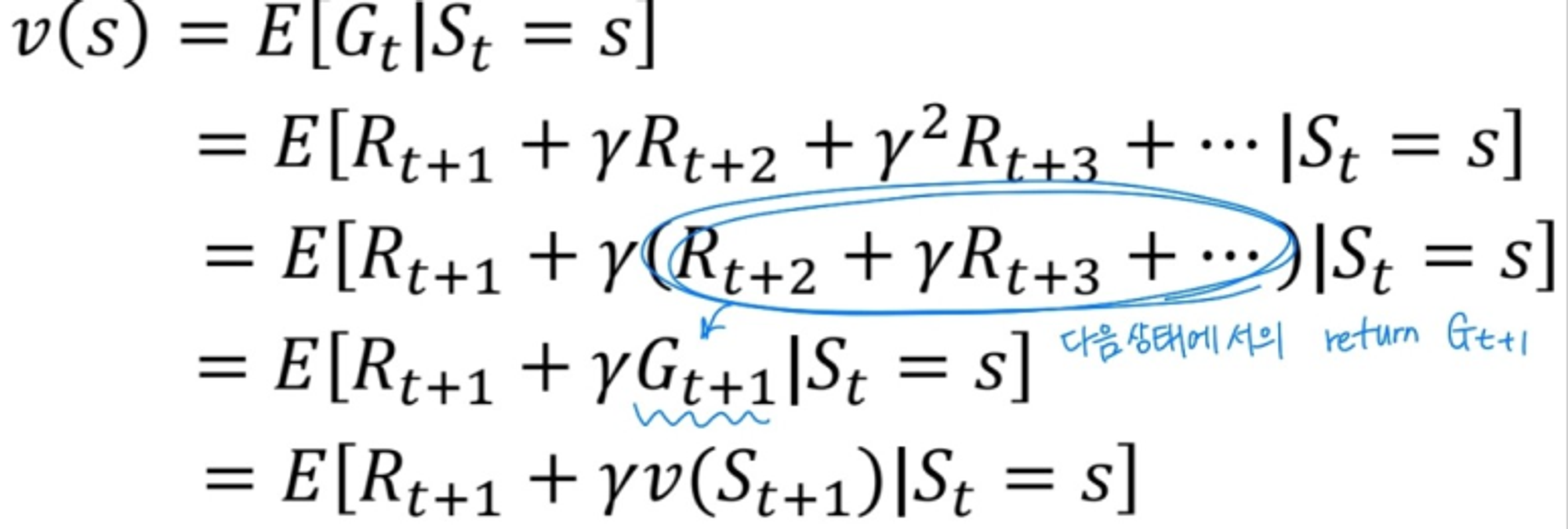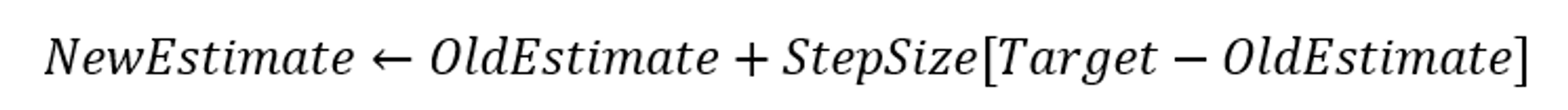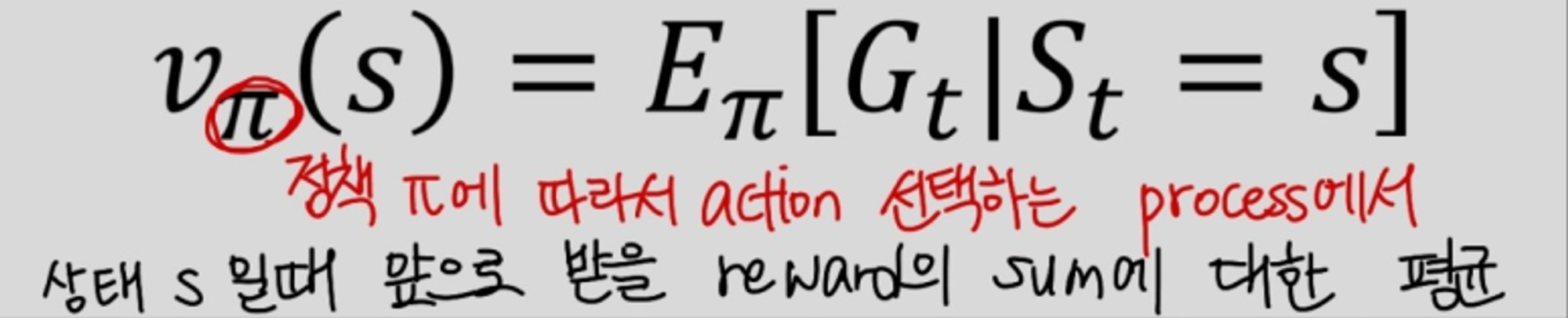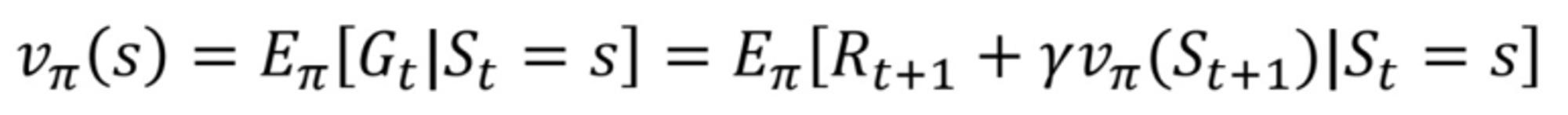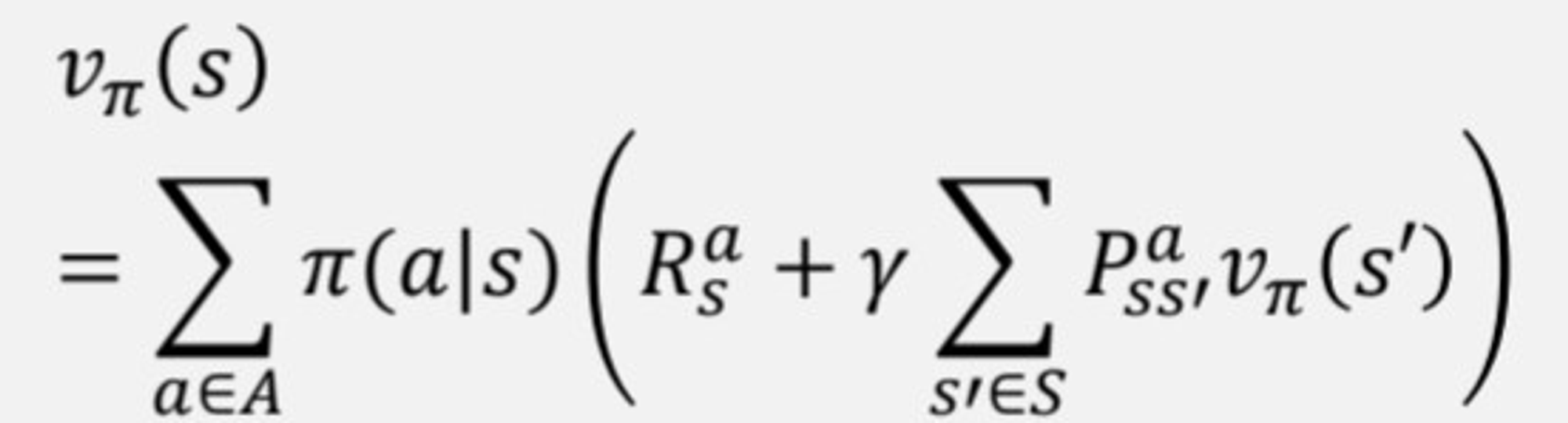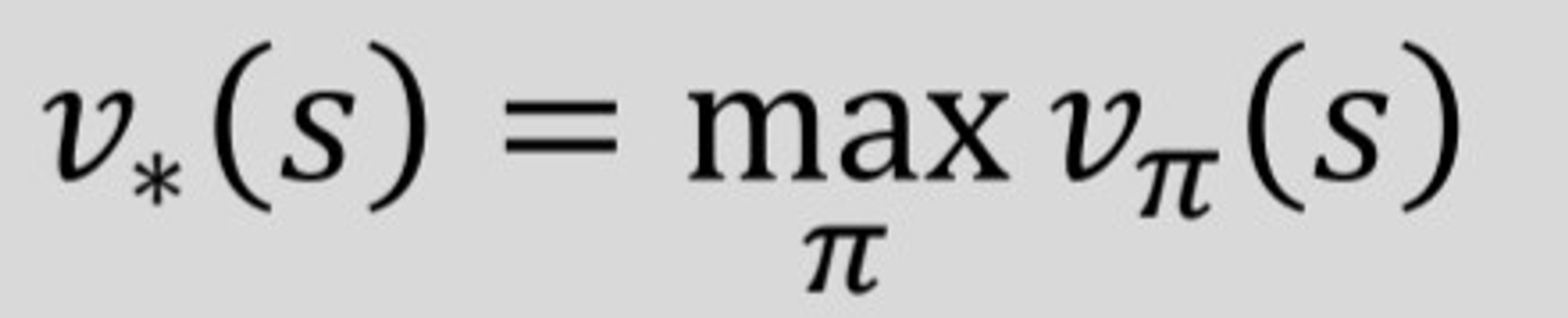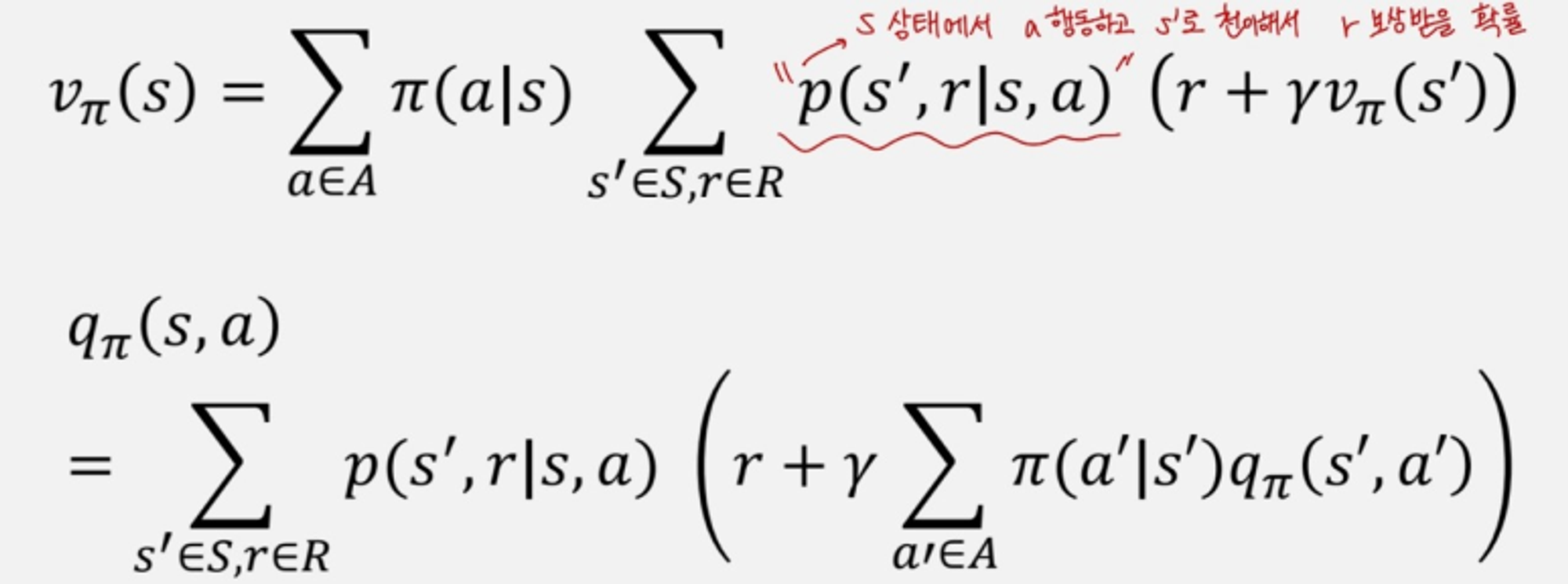Markov Property
과거의 상태가 미래와 전혀 관련이 없고, 과거와 미래가 서로 독립적인 특성을 의미한다.
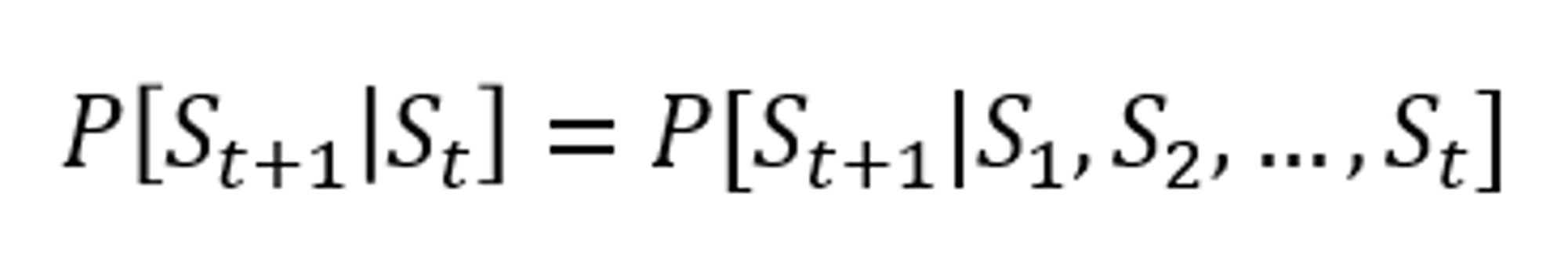
위 수식은 에서의 의 확률이나, 부터 까지 모두 발생한 후에 가 발생할 확률이 서로 같다. 즉 과거의 상태는 관여하지 않다는 것을 의미한다.(memoryless random process) 이러한 Markov 속성을 따르는 process를 Markov Process라고한다.
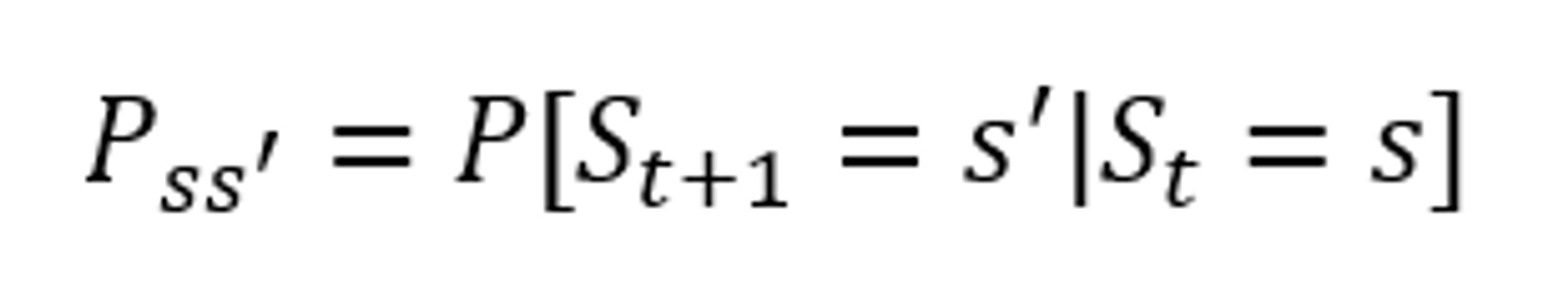
Markov 상태에서 state s 에서 next state s'로 전이할 확률을 위와 같이 표기한다.
Markov Process
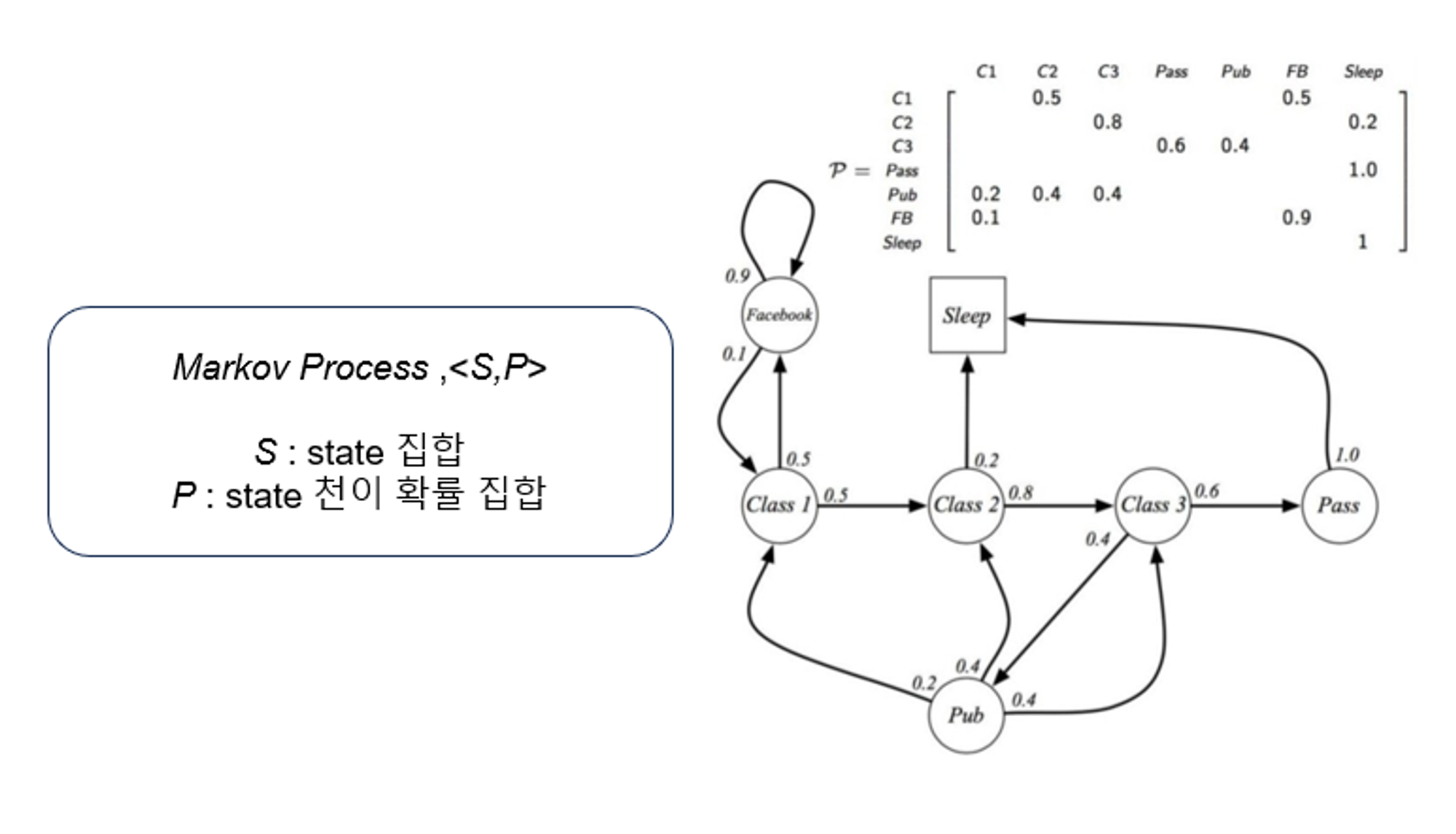
위의 process에서 student는 특정 시간이 지나면 class 1에 있다가 50%의 확률로 Facebook을 하고, 이동한 Facebook을 하는 상태에서 90% 확률로 또 시간이 지나면 Facebook을 하는, state에 관한 집합과 다른 state로 이동할 확률에 대한 집합만 존재하는 다소 간단한 process다. 이전의 Markov property를 지키며, 이전 state가 어떤 state였는지 관계없이 P집합에 있는 transition 확률에 따라 상태가 변하는 것을 알 수 있다.
Markov Reward Process
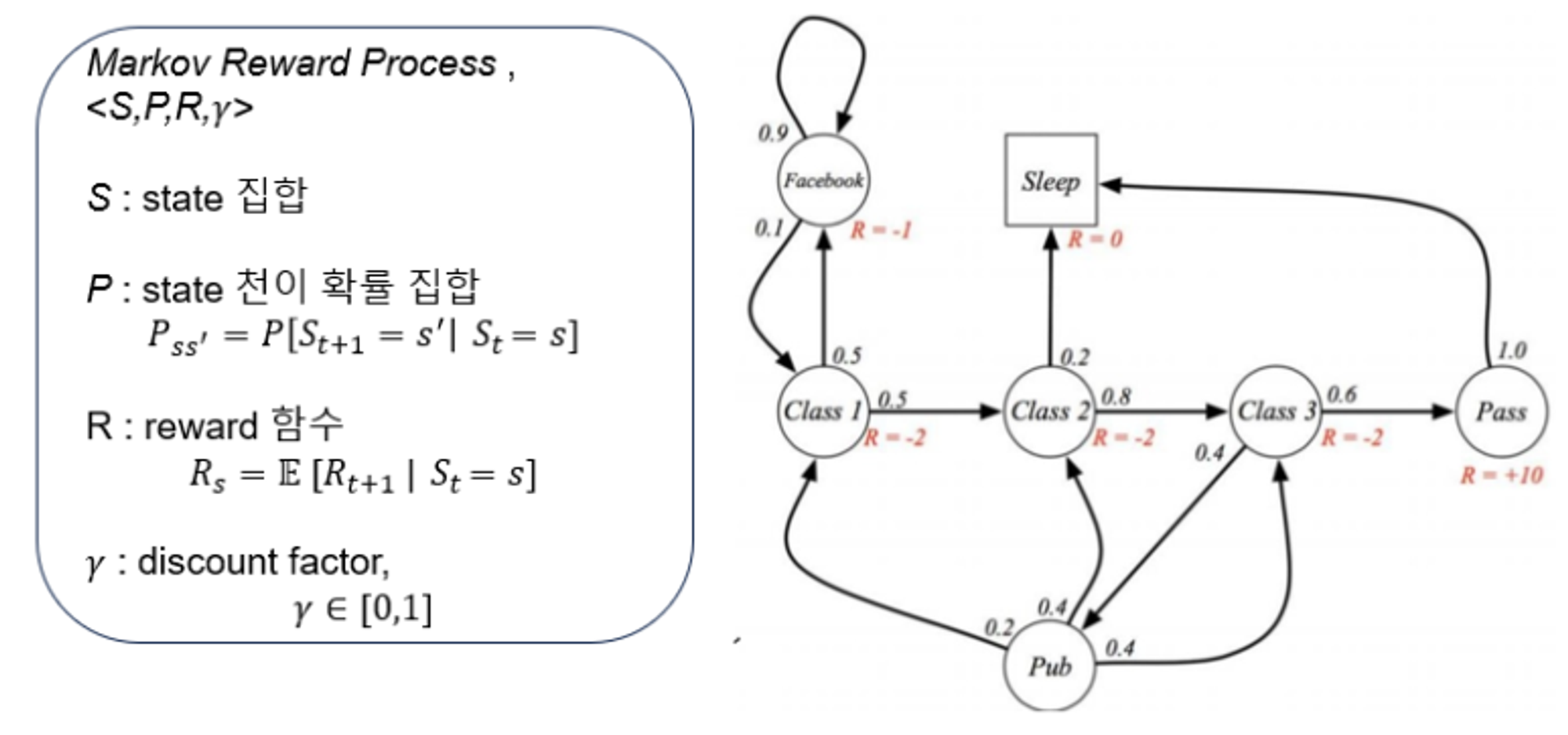
추가된 R과 에 대해 살펴보자.
- : s에서 떠날 때 받게되는 reward (delay되어 지급됨)
- : 눈앞의 state에서의 reward뿐 아니라, 한참 후의 reward에 대해서 반영할때, discount factor로 사용함
Return
time step t에서 episode종료때까지 얻을 수 있는 모든 reward의 합을 의미
여기서 discount factor의 값에 따라 달라진다.
- 일때, 미래의 reward가 즉각적인 reward만큼 중요함
- 일때, 즉각적인 reward만 생각함
Value function
Value function: 현재 state s에서 받을 수 있는 모든 state천이 case에 대한 return값의 평균을 의미한다. 이전에 계산해둔 식을 이용하면 value function에 대해 더 명확하게 정의할 수 있다.
Bellman Equation of Value function (MRP)
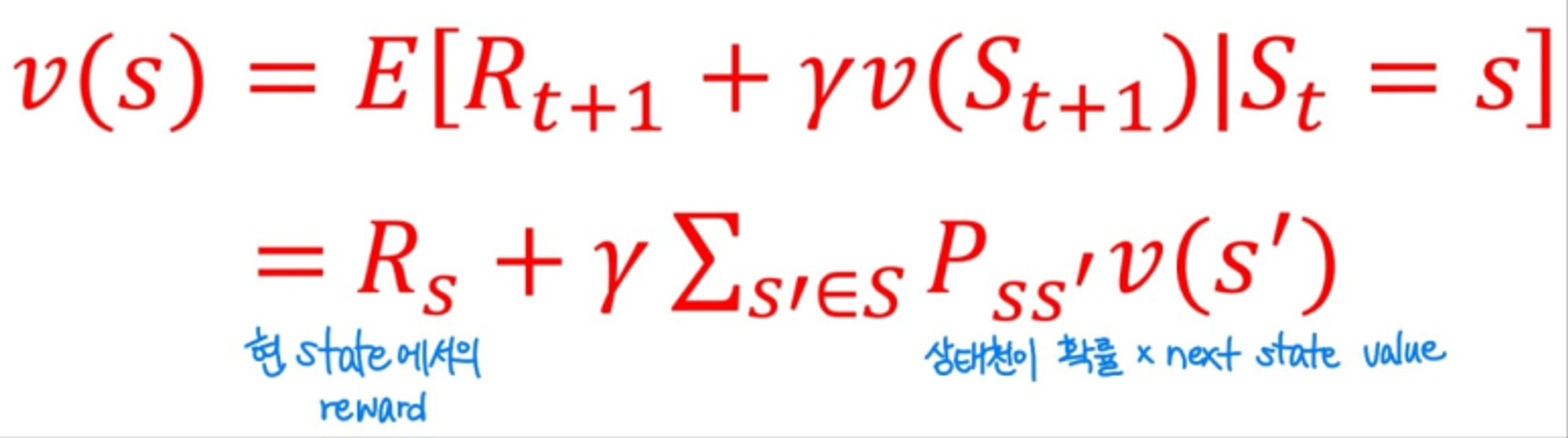
행렬을 사용하면 위와 같이 state value function을 정의할 수 있다.
- : n개의 state가 현재 있는 상황
- : 각 state마다 현 state에 해당하는 reward
- : 현재 state에서 다음 state로 이동하는 각 확률 P 행렬
- : next state에서의 value function
이렇게 결국 역행렬의 연산으로 P,R은 알고있기 때문에, state value를 구할 수 있다. 하지만, n개의 state에 이는 O()의 시간 복잡도를 가지게 된다. 따라서, 이를 iterative form으로 해결하고 행렬 연산은 수행하지않는다.
이전의 Multi Armed Bandit에서의 iterative form
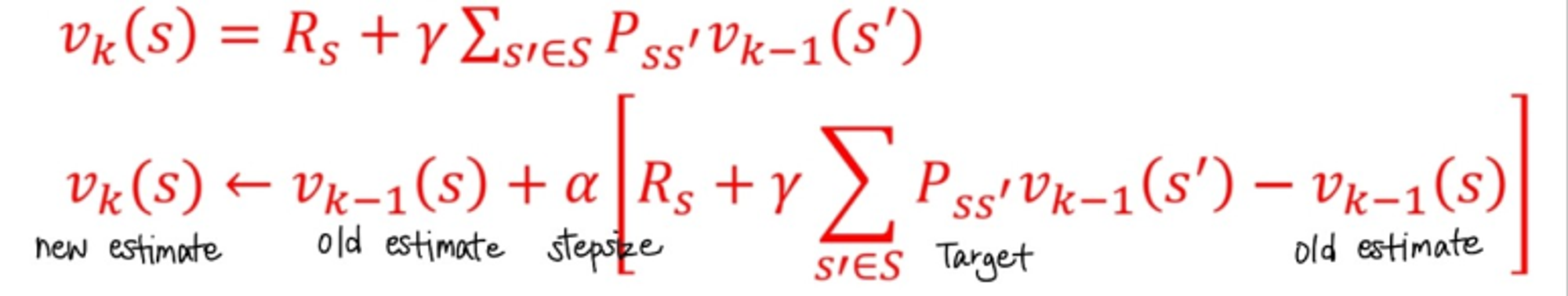
k번째 time step즉, k시간대에서는 next state의 state value를 알 수 없다. 따라서, k-1번째 time step에서의 next state value를 가져와 사용하는 것이다.
Markov DecisionProcess
Markov Reward Process와의 차이점은, state transition , reward 가 있다.
- State transition : s라는 상태에서 a라는 행동을 취했을 때, s'라는 상태로 변할 확률
- Reward : s라는 상태에서 a라는 행동을 취했을 때, 얻는 reward
(a라는 action에 의한 결과가 무조건 한개의 s'이 나오지는 않는다.)
한 action 수행 시, 한 상태로만 천이하는 것을 deterministic하다고 한다. 하지만, 다수의 환경은 그렇지 않다. 예시로 cartpole 문제에서, pole 세우려고 cart를 이동했을 때, 바람 등의 외부적인 이유로 인해서 예상치 못한 state가 될 수 있다. 강화학습 환경에서는 하나의 action에 의해 무수히 다양한 state로 천이될 수 있다. 그리고, reward 또한, 일정하지않고 pdf를 따르게 된다. 따라서 평균으로 정의하는 것이다.
- policy : 각 state에서 어떤 action을 선택하는지 특정화하는 것. 즉, 특정 state에서 어떤 action을 행하는지가 바로 policy이다.
위의 식은 policy의 식이다. policy는 주어진 상태 s에서 행동 a를 선택해서 해당 action을 수행할 확률분포이다. 기존에 있었던 MDP에서 policy 를 추가하게 되면 state transition과 Reward에 해당하는 수식을 수정해야한다.
기존에 있었던 transition 과 reward에 policy를 곱했다.
MDP에서의 state-value function과 action-value function은 아래와 같다.
모두 이전과 다르게 policy 를 따르는 상황에서가 전제된다. MDP의 state value functoin과 action value function에 대한 Bellman expected equation을 적용했다.
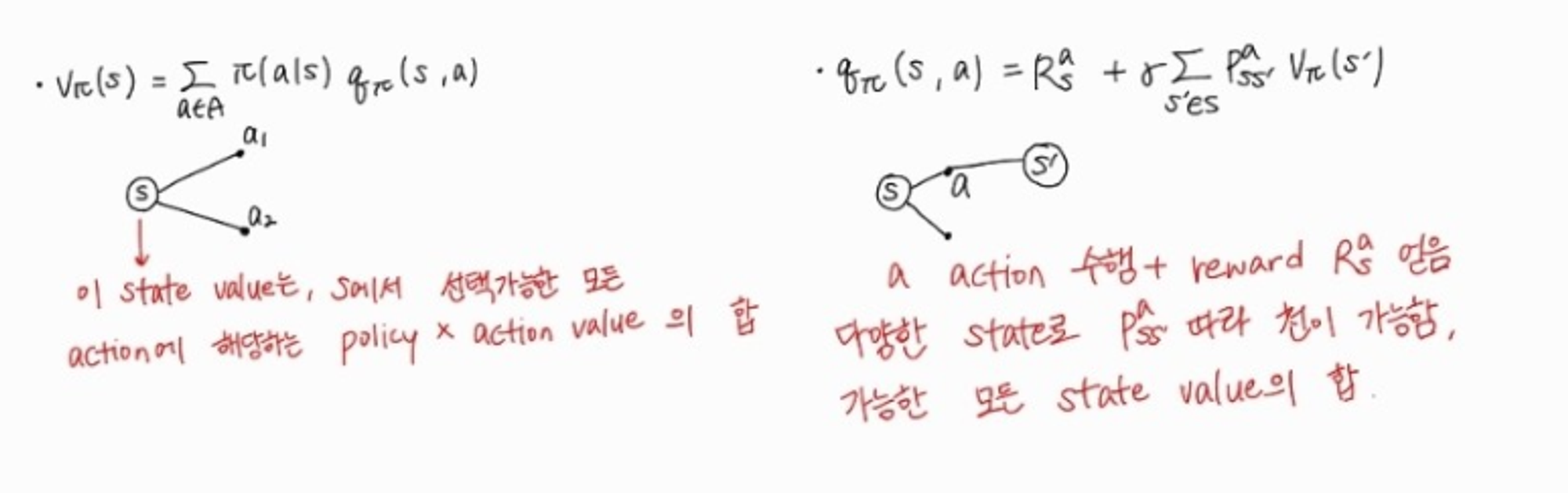
밑의 그림은 state value와 action value의 차이를 나타내는 그림이다.
각각의 state value와 action value에 대한 정의를 다시 정리해보았다. 여기서 각각 서로를 대입해준다면 state value와 action value만으로 이루어진 식을 작성하는게 가능했다.
Iterative form
state value와 action value를 각각 state value만으로 action value만으로 표현이 가능하다. 즉, 나머지값을 알고 있기 때문에, iterative한 방법으로 이전에 Q값을 구했던것처럼 구하는것이 가능해진 것이다.
각각 최적의 policy를 따라 action을 수행했을 때의, 다시말해 최대의 state value와 action value를 얻게 되는 식을 위와같이 정의한다.
이전까지는 reward는 평균값으로 구했었는데, a라는 행동으로 인해 s에서 s'로 천이될때 r을 보상받는 확률로 state value function과 action value function을 정의도 가능하다.
Optimal Policy
optimal policy는 다른 policy보다 value값이 같거나 더 큰 policy이다.
optimal policy일 때 위의 state, action value를 가진다.
위가 바로 optimal policy가 된다. 말그대로 가장 큰 reward만 주는 action만 고르게 되는 것이기 때문에, action value값이 최대가 되는 actoin을 고르는 확률을 1로 하고 나머지는 전부 0으로 고르게 되는것이 바로 optimal policy라는 것을 알 수 있다.
제일 큰 action value만 선택하는 policy이기 때문에, 선택 가능한 행동이 어차피 한개로 정해지고 optimal policy를 따를 때의 action value가 state value와 같아지게 되는 것이다.
max operator를 넣은 수식이라 linear하지 않아서, iterative한 방법으로 구하는 수 밖에 없지만, 위의 두 식은 optimal policy를 따를 때 state value 와 action value이다.
Reference
https://www.notion.so/Markov-Decision-Process-9c7eb05268a043af821818d1fcdcbfed