DQN <4> Dynamic Programming

김동한·2024년 4월 28일

DRL

목록 보기

4/14

글에 들어가기 앞서 간단한 개념을 복기해보자. 현재 다루는 environment는 MDP조건을 만족하는 상황이다.

policy: state에서 action을 선택하는 확률이다.
optimum policy: policy중에서 최대의 return값을 가지도록 선택하는 걸 의미한다.
⚠️ environment와 agent간 행동이 완벽히 모델화 되었을 때 사용이 가능한다.

State s에서 받을 수 있는 return값을 최대가 되게끔 할 때, Bellman Equation

$v_*(s)=max_a\mathbb{E}[R_{t+1}+\gamma v_*(S_{t+1})|S_t=s,A_t=a]$
$=max_a\sum_{s',r} p(s',r|s,a)[r+\gamma v_*(s')]$

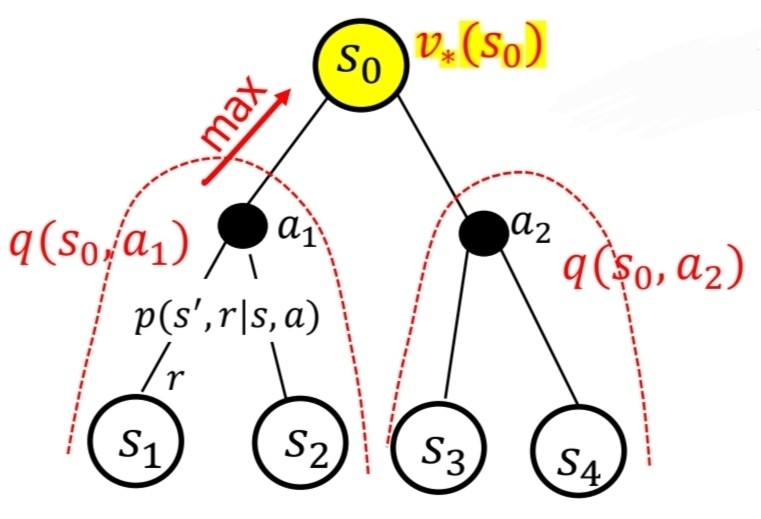
State s에서 a를 선택했을 때, 받을 수 있는 return값을 최대가 되게끔 할때, Bellman Equation

$q_*(s,a)=\mathbb{E}[R_{t+1}+\gamma max_{a'}q_*(S_{t+1},a')|S_t=s,A_t=a]$
$=\sum_{s',r} p(s',r|s,a)[r+\gamma max_{a'}q_*(s',a')]$

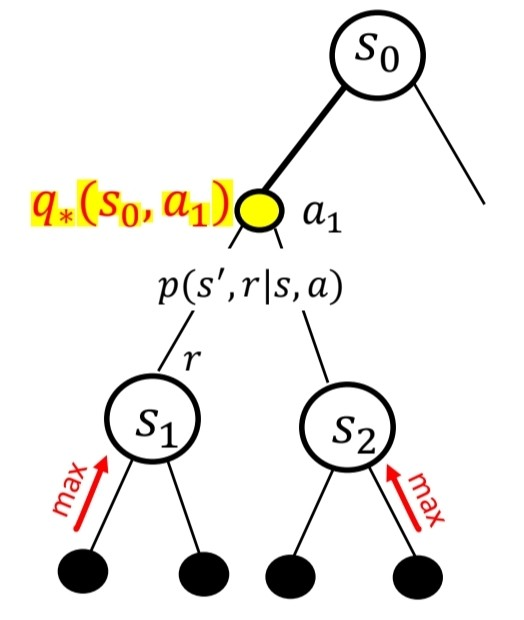
위와 같이, Bellman optimality equations를 작성할 수 있다.

기본적으로, 전지적인 관점이며, Model의 세상에 대해서 모든 것을 알고 있다는 전제를 가지고 있다. $p(s',r|s,a)$ 에서 모든 $s',r,s,a$ 는 알려져있다고 생각한다. Bellman equation을 사용해서 state, action value를 위와 같이 계산할 수 있었다. policy가 존재하는 MDP에서 최적의 policy를 구하기 위해서, 기본적으로 아래의 순서로 접근할 수 있다.

임의로 policy를 어떻게 할지 설정한다. (policy evaluation)

임의의 policy로부터 최적의 policy로 개선해 나가야한다. (policy improvement)

그중에서 policy evaluation에 대해서 먼저 알아보았다.

Policy Evaluation (prediction)

Dynamic Programming이란..?

state value function $v_\pi$ 는 임의의 policy $\pi$ 에 대해서 아래와 같이 계산되어진다.

$v_\pi(s)\dot{=}\mathbb E_\pi[G_t|S_t=s]$
이는 policy와 reward가 확률적인 값이기 때문에 평균값으로 계산한다.
$=\mathbb E_\pi[R_{t+1}+\gamma G_{t+1}|S_t=s]$
$=\mathbb E_\pi[R_{t+1}+\gamma v_\pi(S_{t+1})|S_t=s]$
평균은 확률변수 x 확률값과 같기 때문에 아래와 같다.
$=\sum_a\pi(a|s)\sum_{s',r}p(s',r|s,a)[r+\gamma v_\pi (s')]$

즉, $v_\pi(s),s$ 가 변수인 상태로 linear equation을 작성할 수 있지만, 매우 복잡해서, state의 수가 많아질수록, 선형적인 해결이 힘들어진다. 이를 해결하기 위해서, iterative하게 optimal policy를 찾아가는 방법을 Dynamic Programming이라고 한다.

Iterative method

$v_{k+1}(s)\dot {=} \mathbb E_\pi [(R_{t+1}+\gamma v_k(S_{t+1})|S_t=s]$
$=\sum_a\pi(a|s)\sum_{s',r}p(s',r|s,a)[r+\gamma v_k(s')]$

위와 같이 $v_{k+1}$ 을 이전 iteration에서의 state value값인 $v_{k}$ 통해 구하는 수식으로 표현 가능하다. 여기서, 전지적 시점을 기저에 두기 때문에, $\pi(a|s),p(s',r|s,a),r,\gamma$ 는 모두 알고 있는 상태이다. 따라서, 시간복잡도 측면에서 훨씬 절약가능하기 때문에, iteration method를 사용한다.

여기서 iteration( $v_{k+1},v_k$ )를 저장해둘 배열을 서로 다르게 하면, synchronous
서로 같게하면, asynchronous 방법이 되는 것이다.

이해하기 쉽게 synchronous 와 asynchronous 방법에 대한 예시를 각각 아래 살펴보는게 좋다.

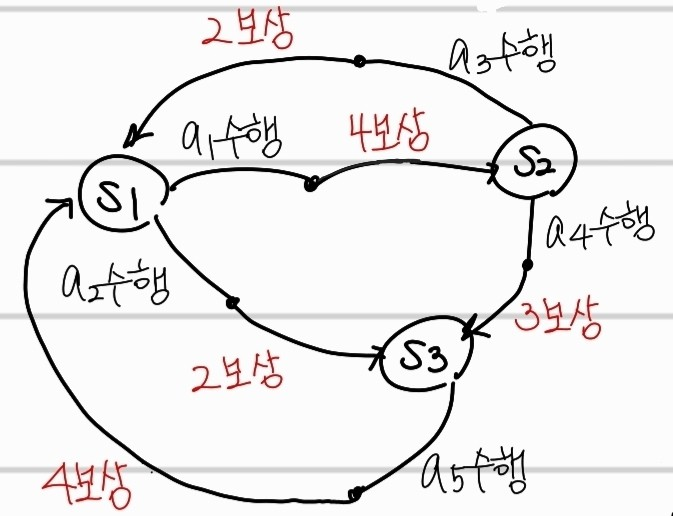위의 transition을 따르며, 간단하게 하기 위해서 아래와 같이 설정했다.

reward: 상수
action의 결과: deterministic
$v_0(s_1)=v_0(s_2)=v_0(s_3)=0$ 로 초기화함
$\gamma$ : 1
$\pi$ : random selection (ex:두개의 행동이 주어지면, 각 50% 확률로 수행)

Synchronous

1번째 iteration
$v_1(s_1)=0.5\times(4+v_0(s_2))+0.5\times(2+v_0(s_3))=3$
$v_1(s_2)=0.5\times(2+v_0(s_1))+0.5\times(3+v_0(s_3))=2.5$
$v_1(s_3)=1\times(4+v_0(s_1))=4$
2번째 iteration
$v_2(s_1)=0.5\times(4+v_1(s_2))+0.5\times(2+v_1(s_3))=6.25$
$v_2(s_2)=0.5\times(2+v_1(s_1))+0.5\times(3+v_1(s_3))=6$
$v_2(s_3)=1\times(4+v_1(s_1))=7$

.
.

Asynchronous

1번째 iteration
$v_1(s_1)=0.5\times(4+v_0(s_2))+0.5\times(2+v_0(s_3))=3$
$v_1(s_2)=0.5\times(2+v_1(s_1))+0.5\times(3+v_0(s_3))=4$
$v_1(s_3)=1\times(4+v_1(s_1))=7$
2번째 iteration
$v_2(s_1)=0.5\times(4+v_1(s_2))+0.5\times(2+v_1(s_3))=8.5$
$v_2(s_2)=0.5\times(2+v_2(s_1))+0.5\times(3+v_1(s_3))=10.25$
$v_2(s_3)=1\times(4+v_2(s_1))=12.5$

.
.
위의 두 예시를 비교해보면 알 수 있듯이, asynchronous 방법을 사용하면 더 빠르게 수렴한다는 것을 알 수 있다. list를 따로 두개 선언한뒤에 이전 iteration을 저장하는게 아니라, 현재 iteration에 해당하는 값이 갱신되었던 적이 있으면, 바로 그 값을 사용하였다. (위의 예시에서 $v_1(s_2)$ 계산 시를 확인해보면 알 수 있다.)

Policy Improvement (control)

임의의 policy $\pi$ 에 대해서 policy evaluation을 통해 state value를 알고 있기 때문에, action value가 최대가 되는 action만 선택하면, 이는 optimal policy를 따른다고 할 수 있다.

$\pi'(s)←argmax_a\sum_{s',r}p(s',r|s,a)(r+\gamma v_\pi(s'))$
$p(s',r|s,a)(r+\gamma v_\pi(s'))=q_\pi(s,a)$

즉 policy evaluation을 통해 state value에 대해서 알고 있는 걸 바탕으로, 행동별 action value를 구할 수 있고, 이 값이 최대가 되게하는 policy로 선택하는 것이다. 이때, 사실 evaluation과 동시에 optimal policy를 고르게끔 하는 것이 가능하다. 각각 policy iteration, value iteration이라고 한다.
policy iteration: evaluation과 optimal policy 구분
value iteration: evaluation과 optimal policy에 대한 구분 없음

policy iteration

이 알고리즘을 살펴보면, policy에대한 evaluation이 모두 마친 이후에 imporvement를 진행하는 것을 알 수 있다.

value iteration

max인 값을 계속 받아오는 것이기 때문에, iteration마다 변하는 최댓값에 의해 policy improvement가 자연스럽게 된다. 한번, value function의 값이 optimal하면, policy에 의해 나오는 값 또한 무조건 optimal한 성질을 사용해서 policy iteration보다 빠르게 optimal bellman equation을 구하는 것이다.