DQN <5> Monte Carlo

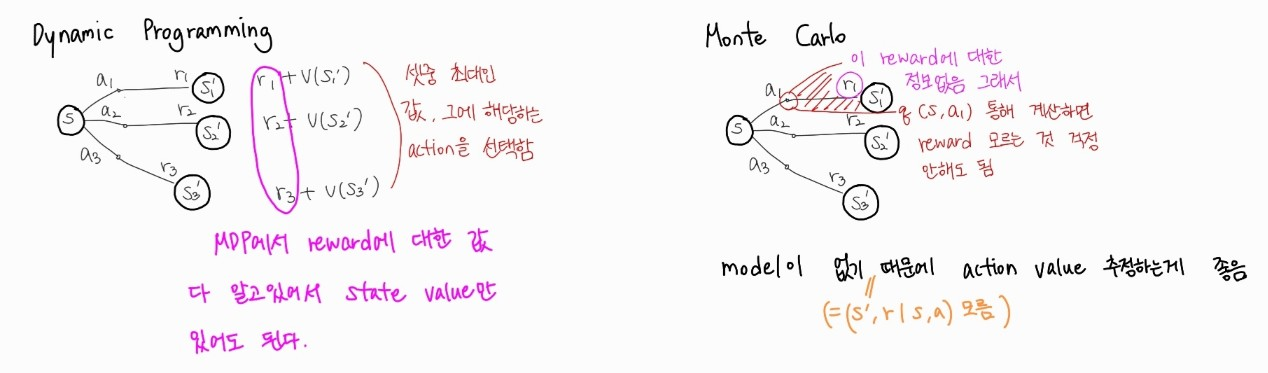
Model-Free Aproach Dynamic programming의 문제점

Dynamic programming은 치명적인 단점이 존재한다. 바로 Model에 대해서 모든 것을 알고 있다는 전제이다. 즉, state transition의 확률(policy), reward의 확률 등 모든 것을 알고 있기 때문에, next state에서의 state value를 알고 있다. 이를 활용해 iterative하게 state value를 update가능하다.

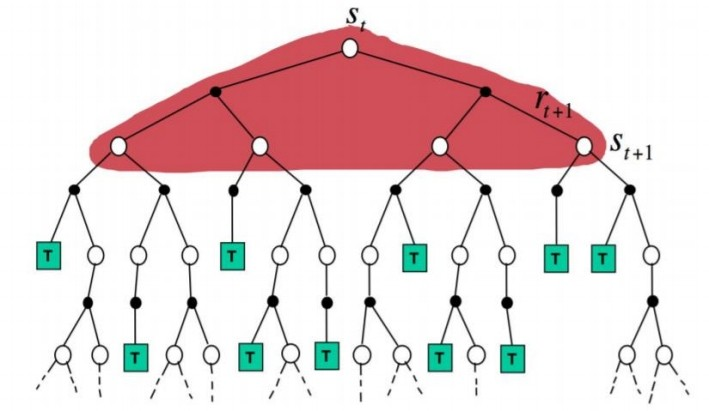
위의 이미지처럼, 어떤 state에서 한 step 지난 후의 모든 state를 사용해서 해당 state value를 update하기 때문에, Full width backup이라는 것을 알 수 있다. 하지만, MDP에 대해 모두 알고 있다는 전제는 현실적이지 않다. 따라서, 실제 강화학습에서는 transition과 reward에 대해서 알지 못하기 때문에, Model free approach에 해당하는, Monte Carlo(MC) method 아니면 Temporal Difference(TD) method를 활용한다.

Monte carlo Method

Monte carlo method의 주요 개념은 바로 sampling backup이다. 이 method에서는 우선 agent가 환경과 상호작용해 sample들을 얻는 과정을 거친다. 이는 $p(s',r|s,a)$ 확률 분포를 sampling하는 것과 동일하다. 여러번의 episode를 terminal state(종료 상태)까지 시행해본뒤, environment로부터 자연스럽게 얻은 sample들을 저장하는 것이다.

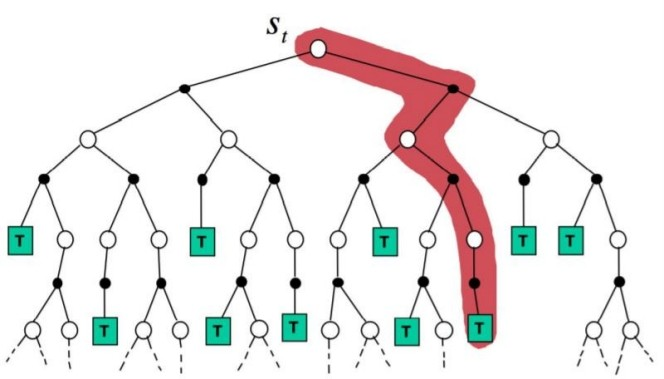
이전 Dynammic programming과 매우 다른 방법으로 state value를 예측하게 된다.

$v_\pi(s)=E_\pi[G_t|S_t=s]$
$E_\pi$:여러 episode에서의 return값의 평균
→iterative form
$v_{k+1}(S_t)←v_k(S_t)+\alpha[G_t-v_k(S_t)]$

iterative 한 방법의 수식에 대해서 이해하기 어려울 수 있다. 꼼꼼하게 수식에 대해 살펴보자.
먼저, $v_\pi(s)=E_\pi[G_t|S_t=s]$ 이 수식에 대해서 알아보자,
Monte carlo method는 terminal state까지 episode를 진행한 후 , 여러 episode를 통해 얻은 state value를 통해서 평균을 내어 state value를 구해야한다. 하나하나 에피소드를 진행하며, 여러 episode에서의 average값을 계산해야한다. 이 과정에서 어떠한 action이 계속 선택되지 않았다면, 해당 action이후의 state에 대한 value를 예측하는데 어려운 문제가 있다.

$NewEstimate ← OldEstimate + StepSize [Target-OldEstimate]$

iterative하게 새로운 값에 대해 예측할때 위의 수식을 따른다. 위의 형태를 그대로 Monte carlo method의 state value estimation에 사용할 수 있다.

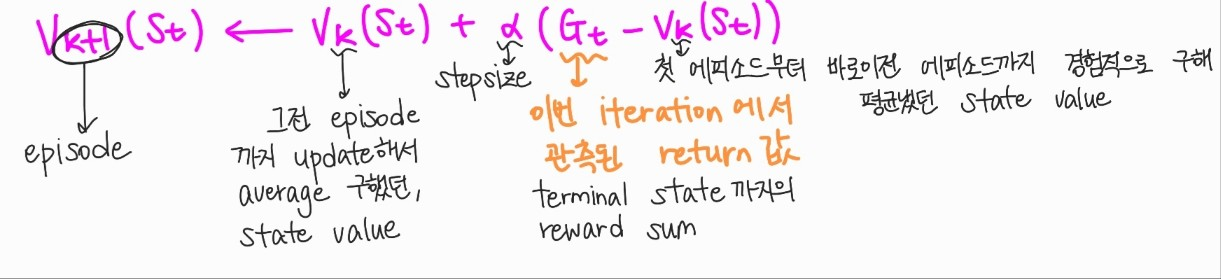
여기서 제일 헷갈릴 만한건, $G_t$값이다. 이는, 이번 iteration에서 관측된 return값을 의미한다. 즉 지금의 episode에서 terminal state까지의 모든 reward들의 sum이다. k번째 episode까지의 state value들에 stepsize $\alpha$와 함께, $G_t$ target return값을 수식에 사용하며, k+1번째 episode의 state value를 계산할 수 있다. Monte carlo method는 두가지 큰 문제가 있다.

• 방문을 아예 하지않는 (action,state)가 존재할 수 있다.
• terminal state가 없는 environment에 적용이 힘들다.

Monte carlo prediction

policy $\pi$ 가 주어진 상태에서 state value에 대해 estimate하는 것은 아래와 같다.
$v_\pi(s)=E[G_t|S_t=s]=E[R_{t+1}+\gamma G_{t+1}|S_t=s]$이다.

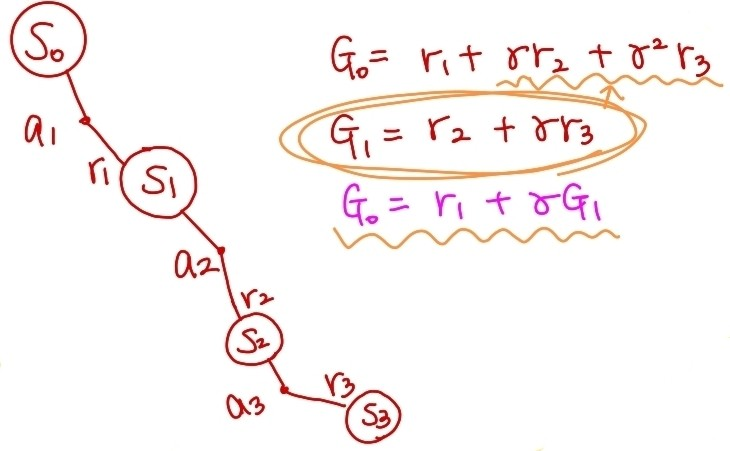
위의 이미지로 보면 이해하기 편하다. $S_0$에서의 $G_t$값은 바로 다음 수행하는 action $a_1$을 한 후의 reward $r_1$ 과 그 이후의 reward들에 대한 discount sum이 $S_0$에서의 return 값이다. 마찬가지로 다음 state들도, 바로 다음 reward와 그 이후의 discount된 reward의 총합이다.

위와 같이 한번 방문했던 state를 다시 방문하는 경우가 생길 수 있다. 이때 $S_0$ 에서의 $G_t$값을 첫번째 방문한 때의 기준으로 할지, terminal state에 가까운 상태를 기준으로 할지 고르는 것에 따라서, First visit/ Every visit Monte Carlo method라고 한다.

• First visit MC : 재방문했던 state 포함시키지않음
• Every visit MC : 재방문할때 state value 덮어씌워서 적용 및 계산.

Monte carlo method는 Dynamic Programming과 다르게 model에 대해서 알지 못하는 상황이기 때문에, reward에 대한 정보가 없다. 따라서, $q(s,a)$를 통해 계산하면 reward 모르는 것을 신경쓰지 않아도 되기 때문에, $(s',r|s,a)$ 를 모르는 상황에서 action value를 estimate해야한다. action value estimate에는 두가지 방법이 있다.

MC with 'exploring starts'

이 방법은 골고루 하기 위해서 임의의 state에서 임의의 action을 첫 시작점으로 잡는 것이다. MC에서는 아예 선택 되지않는 action이 생길 수 있어서 탐험이 필요한데, 이를 보완하기 위해서, episode의 시작점을 여러개로 잡아보는 것이다. 하지만, episode에서는 보통은 동일한 시작점을 가지기 때문에 이런 환경에는 적용하기 쉽지않다.

MC with 'epsilon soft'

이전의 multi armed bandit에서, 슬롯머신 선택하는데 랜덤성을 부여하기 위해 탐험했던 것처럼, epsilon greedy 방법을 사용하는 것이다.

종합적으로 위의 두가지 방법으로 임의의 policy를 따라 여러 episode에 대해서 탐험 및, 경험을 진행해본 뒤, 그 값들을 모아서 action value evaluation을 진행해, max Q(action value) 값을 고르게 policy update를 진행하는 방법으로 model free environment에 대해서, Monte Carlo method를 통해 reward, action value등을 estimation을 할 수 있다.