Temporal Difference

Temporal Difference 즉 TD method는 이전 글에서의 Monte Carlo와 같이 MDP를 Bellman Equation을 활용해서 해결하는 방법 중에 하나이다. 이전 Dynamic Programming과 Monte Carlo의 방법을 혼합하여, bootstrapping 그리고 random sampling이 모두 이루어져 다음 iteration에서의 value를 측정한다 state value bellman equation은 아래와 같다.

$V_{k+1}← V_k(s)+\alpha[R_{t+1}+\gamma V_k(s')-V_k(s)$ ($s'$: next state)

이 수식을 살펴보면, 다른 state에서의 value 추정치를 가져와서 현재 state value를 추정하는 것을 알 수 있다( $V_k(s')$ random sampling). 그리고 기존의 Monte Carlo method와 다르게, 모든 action을 측정하여 return값을 사용하는 것이 아닌, 임의의 policy에 의한 action 1개에 의한 리워드를 사용하는 것을 알 수 있다($R_{t+1}$ bootstrapping).

Temporal Difference(TD) learning은 아래와 같은 여러 이점이 존재한다.

• 빠르게 policy improvement가 가능하다.
• model free method로 MDP내에서의 여러 조건(transition, policy, reward)를 몰라도 적용 가능하다.
• terminal state가 없는 simulation에서도 적용이 가능하다.

---

지금까지의 상태가치 V(s)에 대해서 DP방법부터, TD방법까지의 여러 수식을 비교하면 아래와 같다.

V(s)와 Bellman Equation 이용한 solutions

V(s)에 대한 수식

$V(s)=E[R_{t+1}+\gamma R_{t+2}+ \gamma^2 R_{t+3}+...|S_t=s]$

Dynamic Programming

$V_{k+1}(s)←\sum_a\pi(a|s)\sum p(s',r|s,a)[r+\gamma V_k(s')]$

Monte Carlo

$V_{k+1}(s)←V_k(s)+\alpha [G_t-V_k(s)]$
📌 $k,k+1$ 각각 이전 에피소드, 현재 에피소드를 의미한다. $G_t$ 즉, 한 episode를 끝까지 실행해 observe한 reward값을 얻고 이를 target value로 생각한다.

Temporal Difference

$V_{k+1}(s)←V_k(s)+\alpha [R_{t+1}+\gamma V_k(s')-V_k(s)]$
📌Monte carlo method와 유사하지만, $G_t$ 부분에, $R_{t+1}+\gamma V_k(s')$가 target value로 사용된다. 이 target value는 k episode에서의 "next state value와 current state 에서 action a 이후 얻는 $R_{t+1}$ 리워드"를 사용하는것을 알 수 있다.

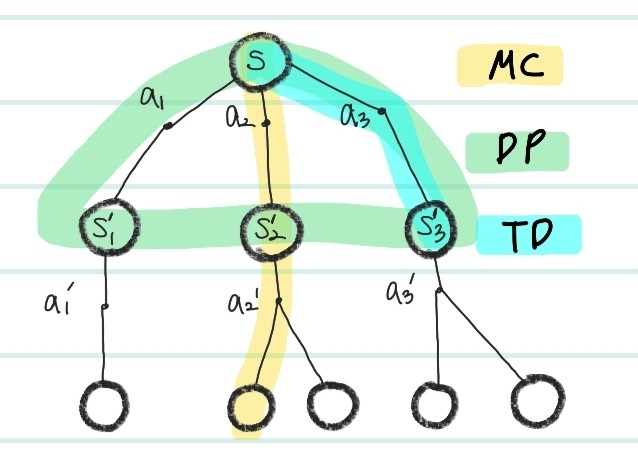
이를 그림으로 나타내면 아래와 같다.

• MC : episode의 끝까지 탐색
• DP : policy에 의한 다음 모든 action선택에 대한 정보 이용 (Model based)
• TD : policy에 의해 임의로 선택한 action에 대한 reward 이용

이제 Temporal Difference learning에 대해서 자세히 그 종류와 함께 공부해보자.

Temporal Difference learning에 대해서

Policy Evaluation

앞선 설명과 같이 td update에서는 bootstrapping과 random sampling 두가지를 모두 사용한다. 각각의 특성은 간단하게 생각하면 아래와 같다.

• Bootstrapping
  이전의 측정값을 사용하여 다음 값을 추정하는 것. in DP
  in TD:
  $V_{k+1}(s)←V_k(s')$ 사용해서 값 추정함.
• Random Sampling
  임의의 policy를 선택, 해당 action에 대해서만 측정한 값 사용. in MC
  in TD:
  $V_{k+1}←R_{t+1}$ 사용해서 값 추정함. 이는 한개의 임의의 action a를 수행했을때 얻는 reward임.

최종적으로 TD 방식은, bootstrapping과 random sampling 두가지의 특성을 모두 사용해 DP,MC에서의 방식을 골고루 섞어서 구현한 것이다. 정리하면 아래와 같다.

TD policy evaluation의 이점

• TD 방법은 우선, model free한 방법이기 때문에, 환경의 정보가 필요가없다. 실제로 모델이 action을 수행하고 얻는 리워드만 제공되면 계산이 가능하다. 이말은 DP와 다르게 state transition 등의 정보가 필요없다는 뜻이다.
• 최종 결과가 나오기 전에 update를 한다. 즉 update하는 것이 빠르다. MC는 한 에피소드가 모두 종료 되어야 update가 가능했지만, TD방법은 그렇지않다. 또한, terminal state가 등장하지않는 simulation에 대해서도 적용이 가능하다는 장점이 존재한다.
• 두번째 이유 덕분에 더 적은 메모리를 필요로 하고, 더 작은 peak computation을 요구한다.

MC와 TD의 converge(수렴) 비교

MC와 TD 모두 수렴하는 것은 fact이다. 하지만 무엇이 더 빠를까?? 바로 TD이다. 왜냐하면 MC는 에피소드마다 모두 수행해야하고, 충분한 양의 에피소드가 쌓여야 수렴하기 때문이다. 물론, MC는 추정치가 아닌 실제로 얻은 값 $G_t$를 사용해서 더 정확한 값으로 수렴 가능하지만, 현실적으로 무한히 수행하는 것은 컴퓨터 환경에서 불가능에 가깝다. (한 1년 컴퓨터를 켜놓을 수는 없으니까) 따라서, 조금 bias가 존재하지만 더 빠르게 수렴하는 TD method를 많이 사용하는 것이다.

What about using Action Value??

여기서 한가지 의문점이 든다. action을 수행한 후 얻는 reward값 r은 사실 확률값으로 정해진 값이 나오지않는다고 하지 않았던가?? 맞다. 예를 들어서, 슬롯머신을 사용하면, 그 reward는 당연히 확률 분포로 나온다. 따라서, state value를 사용하는 것보단, action value를 사용하는 것이 좋다. state value와 다르게, action value는 action마다의 가치를 알 수 있다. 간단하게 아래의 그림을 보면,

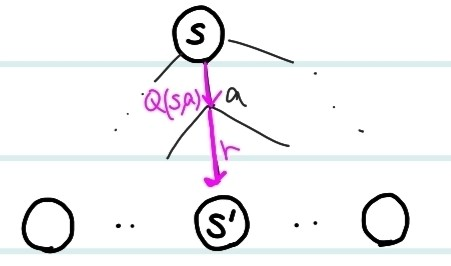next state인 s'과 s 사이에서 reward r값을 state value $V(s')$과 $V(s)$만 가지고 측정하는 것은 불가능하다. 따라서, $Q(s,a)$값을 사용한다. $Q(s,a)$는 기본적으로, s라는 state에서 a라는 action을 수행했을 때 얻는 가치 즉 reward값이기 때문에, 더 정확한 예측이 가능해지는 것이다. 이 값을 바로 Q value라고 하는 것이다.

최적의 policy를 구축하는 것을 최종 목표로 하여, TD policy evaluation을 하고, improvement 하는 것이다. policy improvement는 target과 current값의 차이인 loss를 최소화 하는 것을 목표로 policy를 수정해 나가는 것이다.

여기서 on policy, off-policy방법에 의해 TD method는 SARSA와 Q learning으로 나누어지는데, 이는 다음 글에서 알아보자.