기존의 다른 방법

기존의 DQN: Epsilon-Greedy Algorithm을 사용해 exploration을 수행

Prioritized Experience Replay: buffer에 저장되는 각 transtition에 대해서 우선순위( ${TD}_{error}$ 가 클수록 우선순위가 큼)를 두어, batch로 뽑을때 반영하는 방법이다.

Noisy added fully connected layer

Noisy network는 신경망의 가중치에 잡음을 추가하는 것이다. epsilon greedy method는 현 state와 전혀 상관없이 random한 것을 적용하지만, Noisy network는 state에 어느정도 dependent한 값을 적용 할 수 있다.

• 기존의 fully connected layer : $y=w_{(q,p)}x+b_{(q)}$
• Noisy fully connected layer : $y=(\mu^w_{(q,p)}+\sigma^w_{(q,p)}\ \odot \epsilon^w_{(q,p)})x+\mu^b_{(q)}+\sigma^b_{(q)} \odot\epsilon^b_{(q)}$

Element-wise 곱

$w→ \mu^w+\sigma^w \odot\epsilon^w$ , $b$ → $\mu^b+\sigma^b \odot\epsilon^b$ $A_{\space shape\space of\space A}$

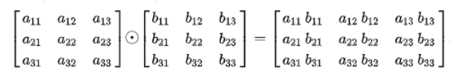
( $\sigma$: noise parameter $\epsilon$ : noise variable $\mu$: 잡음을 더하기 전의 w와 b)

noise variable은 gaussian 분포를 따르는 변수이고, 이를 noise paramter를 통해서 scaling함.

$\varepsilon$ (noise variable)

Gaussian distribution에서 noise를 추출해 이를 활용해서 $\varepsilon$의 값을 정한다.

1. Independent Gaussian Noise (A3C)

Gaussian distribution에서 p*q → $\varepsilon^w$ 개 q → $\varepsilon^b$ 개의 noise추출

• 직관적으로 gaussian distribution 에서 필요한 shape만큼의 noise를 추출함
  Initialisation parameters of noisy networks>
  

---

2. Factorised Gaussian Noise (DQN)

Gaussian distribution에서 p → $\varepsilon_p$ 개 q → $\varepsilon_q$ 개의 noise추출

• p, q개 만 distribution에서 추출한 뒤, 연산을 통해 noie variable의 shape에 맞춤
• $\varepsilon^w=f(\varepsilon_p)\otimes f(\varepsilon_q), \space \varepsilon^b=f(\varepsilon_q), \space f(x)=sin(x)\sqrt{|x|}$
• q*p개 p개의 noise를 추출하는 과정이 오래 걸리기 때문에 p, q개만 추출한 뒤 , $f(x)$를 사용해 $\varepsilon^w$과 $\varepsilon^b$를 구한다.
  Initialisation parameters of noisy networks>
  

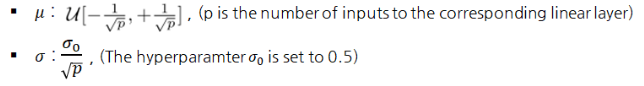
결론

• DQN에선 Factorised Gaussian Noise를 사용해 Noisy Net을 구현한다.
• action 선택시 weight에 더해진 noise 덕분에 random한 action을 고를 수 있게 된다.
• Agent가 자동적으로 noise의 정도를 조절한다. (noise parameter를 통해서)
• 지나친 state correlation이 생기는 것을 막기 위해 target network의 noise와 online network의 noise를 각각 생성한다.
• 결론적으로 강화학슴 알고리즘이 noise의 정도를 결정하기 때문에, hyperparameter의 tuning의 필요를 줄여주는 효과가 있다.
  
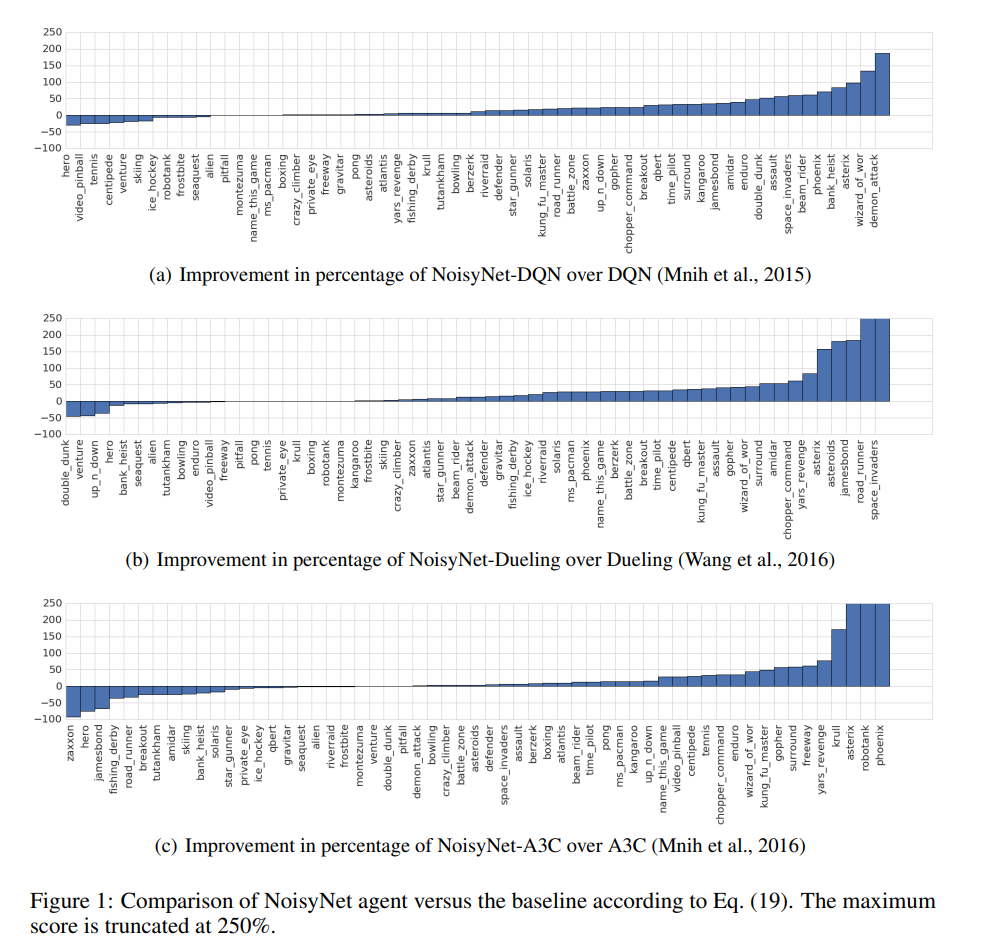
  Noisy network를 적용한 적용한 경우 성능이 대체로 더 좋아졌다.