자연어 생성에서 Decoding 과정
자연어를 생성하는 모델은 입력문장 x에 대해 문장 y를 출력하는 모델이다. (이때 x와 y의 관계는 한글로 된 글-영문 번역글 등이 존재한다) 학습이 완료된 이상적인 언어모델(LM)은 입력문장 x가 주어질 때, 다음으로 예측할 단어나 문장으로 확률이 가장 높은 y를 선택하게된다.
그렇다면, 가장 확률이 높은 y는 어떻게 선택해야할까?
Exhaustive search
모든 조합에 대해서 을 기준으로 가장 확률이 높은 문장을 선택하게 되는 것이다. 이는 큰 문제점을 가지고 있다.
Vocabulary의 크기가 v라고 가정하자. y 단어를 t번 예측할 때, 각 단어가 v의 크기를 가진다. 따라서, 개의 문장에 대한 계산이 필요하다. 즉, 계산량이 많아진다. 그리고 y를 예측할때의 수식을 한번 살펴보자
위의 식에서 최적의 를 한번에 찾는 것은 매우 힘들다. 하지만 조건부확률의 연쇄법칙을 사용해서 이를 분해할 수 있다. 아래는 가 조건부 확률일때의 분해 과정이다.
- 조건부 확률 연쇄 법칙
4개의 확률이 조건부 확률을 가질때 위처럼 표현할 수 있다. 위의 연쇄법칙을 활용해서 수식을 분해해보자.
-
기존 수식
-
예측한 y들을 각각 조건부 확률의 기저로 넣어서 연쇄법칙을 통한 수식 분해
-
Product 기호를 사용한 표현
즉, 이전 단어의 확률을 고려해서 다음 단어를 예측하는 Auto-regressive LM을 활용하게 된다. 그렇다면, 를 최대화하는 y는 뭘까?
Greedy Decoding
매 Time-step마다 가장 높은 확률값을 갖는 Token을 다음 Token으로 선택하는 것이다.
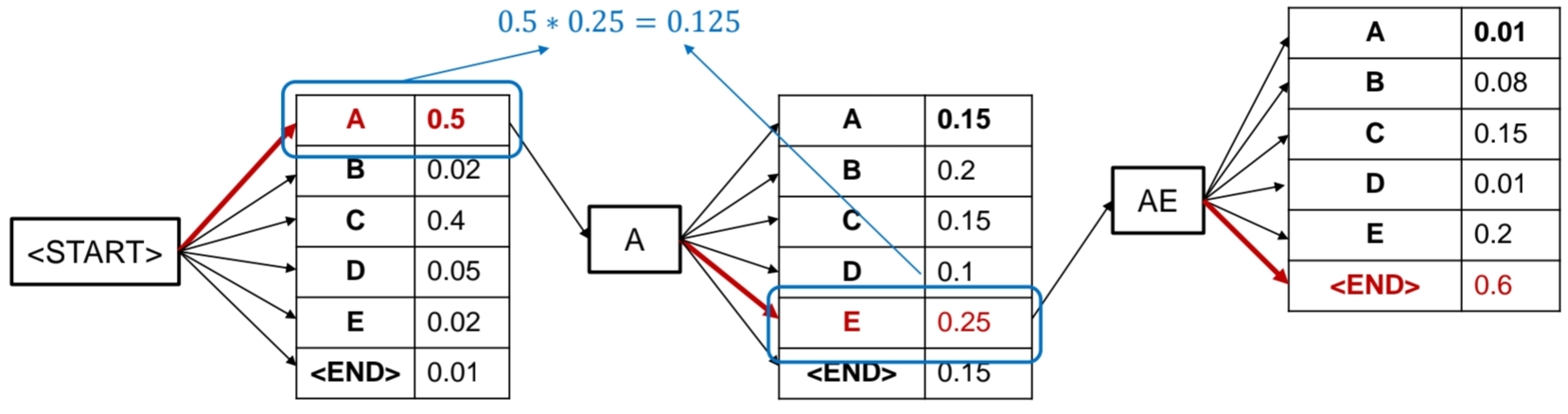
위의 사진과 같이, 무조건 확률이 현재 기준으로 가장 높은 단어를 선택하는 방법이다. 하지만, 이는 치명적인 단점이 있다.
현재 선택하는 Token이 다음 Token 선택시 확률에 영향을 준다는 것이다. 이는 아래와 같은 상황이 생길 수 있음을 의미한다.
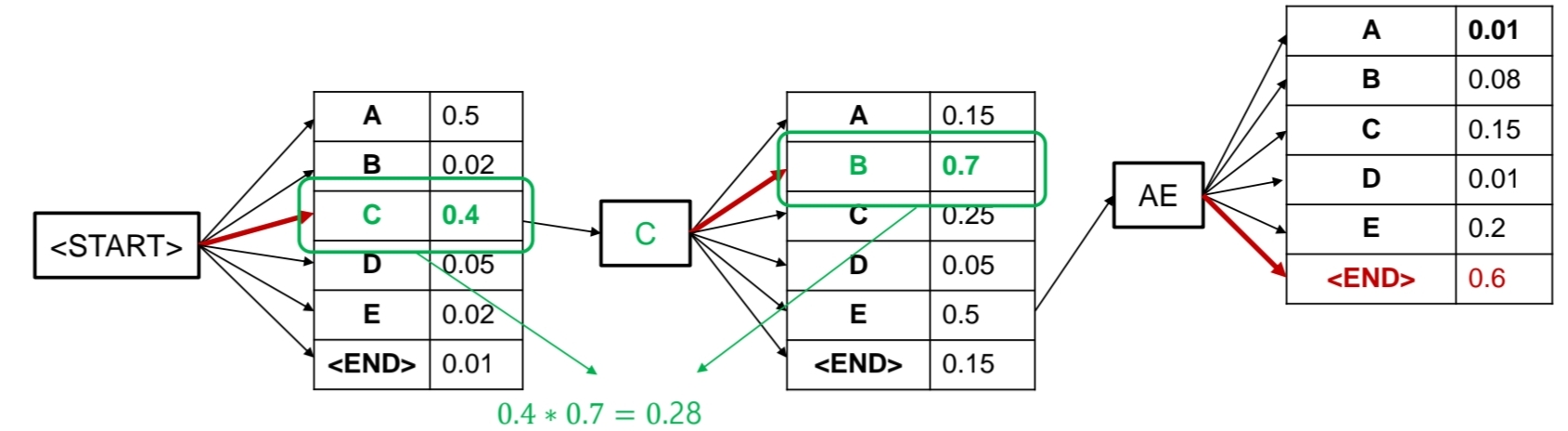
위와 동일한 상황에서 C를 선택할경우 다음 단어는 B가 가장 높은 확률로 두 단어의 생성 확률은 0.28 기존의 0.125보다 클 수 있다는 것이다.
를 근사하는 방법일 뿐 정확한 최적해를 보장하지 않는다는 것이다.
Greedy Decoding은 <END> token을 선택할때까지 token을 생성하게 된다.
Beam Search
해당 방법은 매 Time-step마다 k개의 후보 단어를 생성한다. 이때 k를 Beam size로 부른다. 후보 단어에서 선택되는 단어는 단어의 Score에 대한 비교로 이루어진다. score는 아래와 같이 계산된다.
기존의 에서 log를 붙인 형태이다
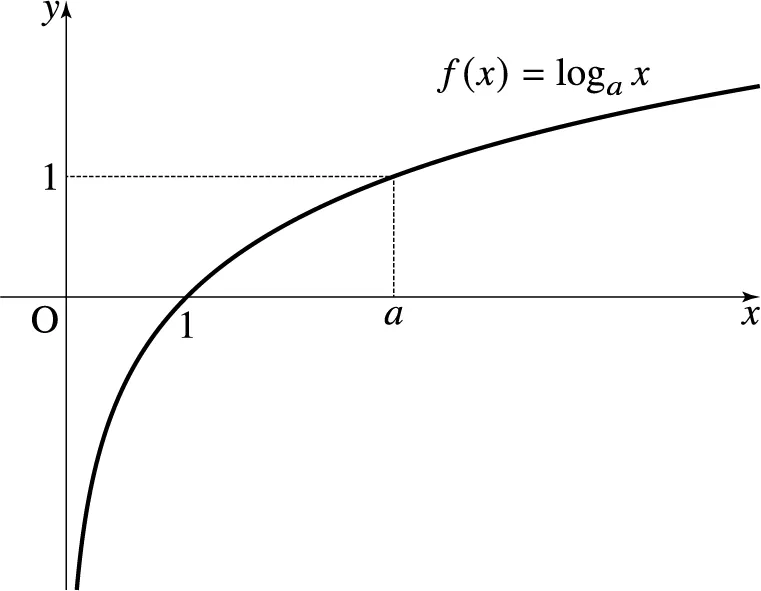
log함수의 그래프 개형은 위와 같은데, 이는 즉 Score는 모두 음수라는 것을 의미한다. (Softmax함수를 거친 P의 값은 무조건 0~1사이의 값이기 때문). 그래도 더 0에 가까운 음수일 수록 더 높은 score로 생각할 수 있다.
즉, Token을 생성할 때마다 score가 높은 k(Beam size)개를 선택하는 것이다. Beam Search 방법은 각 Beam마다 서로 다른 time step에서 <END> token을 선택할 수 있다.
생성이 끝난 갈래는 제외하고, 나머지는 계속 후보를 유지하면서 생성하게 되는 것이다. 그리고 최대 sequence길이를 설정하게 되는데, 이에 도달하게 되면 Decoding이 종료된다.
Beam Search 예시
beam size가 2일때를 예시로 beam search를 통한 decoding을 살펴보자
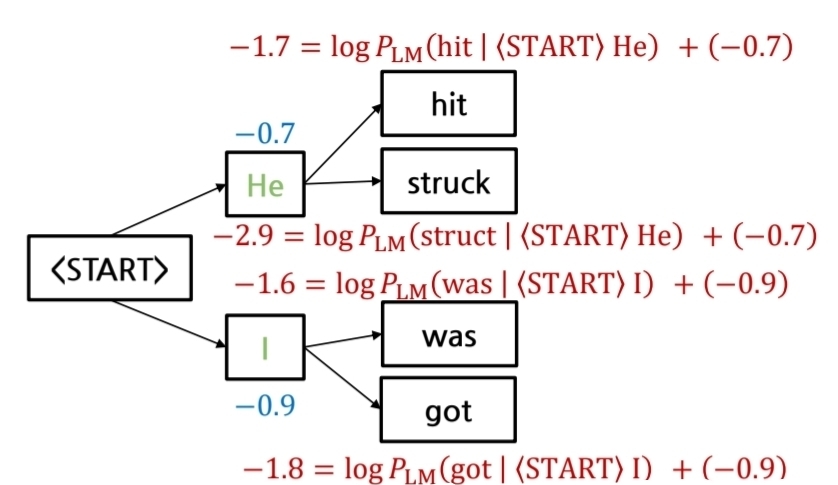
최초로 He와 I가 가장 높은 확률이 나왔다고 가정하고, 각 token별로 다음 k개(2개) 후보에 대한 확률을 계산한다. 이때 확률은 당연히 조건부 확률로 계산한다.
그리고 log를 취했기 때문에 이전에 계산해서 얻은 값은 +로 추가한다. 위의 계산 결과의 경우
hit : -1.7 struck : -2.9 was : -1.6 got : -1.8로 나왔다. 이중에서 다음 단계의 token 확률들의 비교는 hit와 was만 하게 되는 것이다.
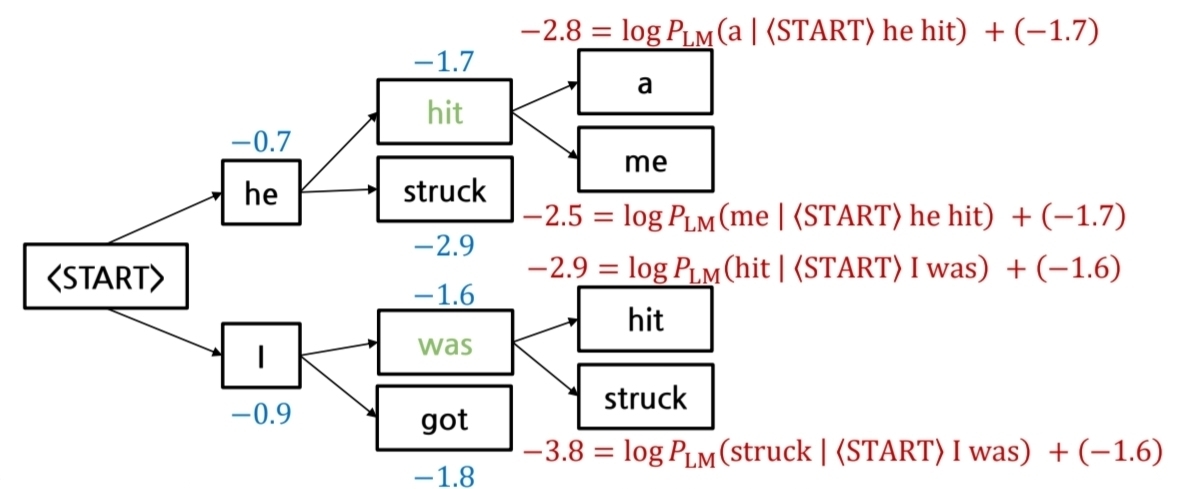
총 개의 후보 중에서 score가 가장 높은 k개를 선택하게 되는 것이다.
최종적으로, 가장 확률이 높은(0에 가까운 token)이 나오게 된 경로를 출력해서 문장을 완성한다.
생각해보면, 아무리 작은 값이더라도 계속 더해지면 음수가 더 커질 수 있다.(0에서 멀어진 더 작은 음수가 될 수 있다.) 따라서, 긴 문장은 무조건 낮은 확률이 될 수 있다. 이를 어느정도 완화하기 위해서 길이에 대한 정규화를 진행한다.
위처럼 t로 정규화를 진행한다. 즉 길어진 문장일수록 t가 커져 어느정도 값을 줄여주는 것이다.
하지만, Beam search는 반복에 매우 취약하고, 사실 인간은 무조건 확률이 높은 단어만을 쓰진 않기 때문에 가끔 쓰는 단어를 다양하게 구사하는것이 힘들다.
Sampling
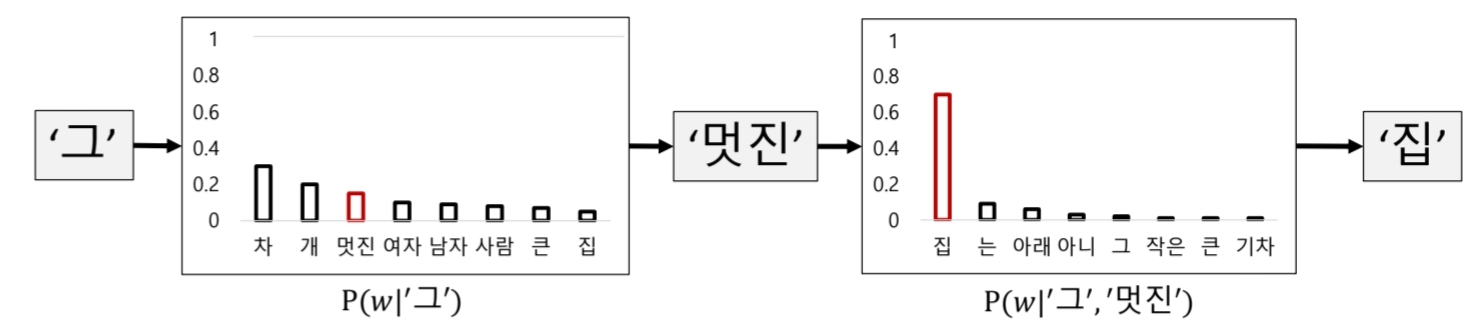
확률이 낮은 단어도 가끔 선택하게 된다면 어떨까? 사실 강화학습에 대해서 공부할때도 무조건 reward를 큰 action만 하지않게끔 epsilon greedy 기법을 사용하곤 한다. 확률이 낮은 단어가 선택될 수도 있게끔 확률 분포에 따라서 단어를 random sampling하게 된다.
위의 예시의 경우 차가 제일 높은 확률이지만, 멋진이 선택되기도 한다는 것을 보여준다.
Temperature
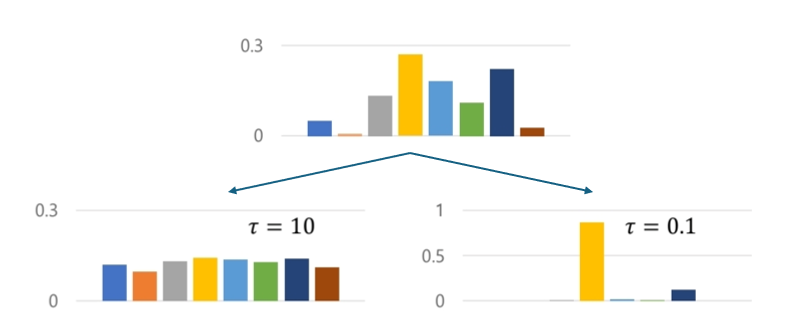
temperature는 언어 생성 모델에서 다양성과 정확성을 조절하는 parameter이다. 이는 실제로 학습과정에서 사람이 설정하는 값으로 클수록 다양한 표현을 선택할 수 있게끔 uniform 분포로 변화한다. 수식은 아래와 같다.
가 여기서 temperature에 해당하고, 이 값이 0이면 완전 Greedy decoding과 동일해진다.
Top-k Sampling
Top-k Sampling은 확률분포에서 어느정도 과감성에 제한을 두는 것이다. 너무 터무니 없이 작은 확률을 선택하면 성능이 떨어질 수 있기 때문에 k개의 단어만 선택해서 sampling을 수행하는 것이다.

이렇게 개수로만 sampling에 제한을 두게 되면 하지만, 확률로 막상 따져보면, 비슷비슷한 값들도 너무 많고 실제로 너무 작은 확률도 포함이 될 수 있다. 따라서, 개수가 아니라 실제 확률의 합으로 sampling을 제한을 두는 방법이 제안됐다.
Top-p Sampling
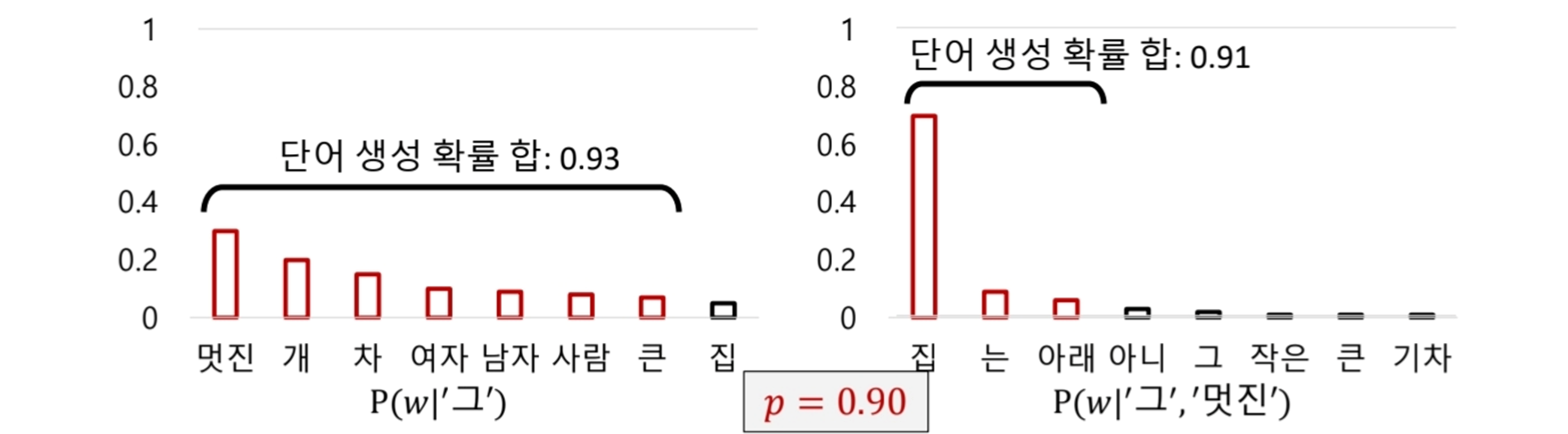
Top-p sampling의 경우 단어 생성 확률의 합이 p가 될때까지의 후보 단어를 선택해서 sampling하는 방법이다. 확률 분포가 평평하면 많은 단어가 후보로 포함되고, 뾰족하면 적은 단어만 후보로 포함되게 된다.
Reference
chatgpt
https://settlelib.tistory.com/52
https://velog.io/@mmodestaa/%EB%94%94%EC%BD%94%EB%94%A9-%EC%A0%84%EB%9E%B5-Greedy-Beam-Search-Random-Temperature-Top-K-Nucleus