인공지능은 x값(input)과 파라미터화된 함수 H를 통한 y값(output)으로 target값을 예측하는 것이다. 이때, 예측한 결과인 output과 target값 사이의 오차가 바로 loss이다. 다양한 방법으로 target값을 예측하고 loss를 정의하는 식도 다양하다. 차례로 알아보자. 일단 간단한 인공지능 모델인 linear regression에 대해 소개한뒤, 이 모델의 loss에 대해서 이야기해보며, loss의 기본적인 형태부터 시작하겠다. 만약 loss function에 대해 잘 안다면, 바로 SGD로 넘어가도 좋다.
linear regression
선형식으로 표현 가능한 hypothesis(가설) 모델을 세우는 것이다. 식은 아래와 같다.
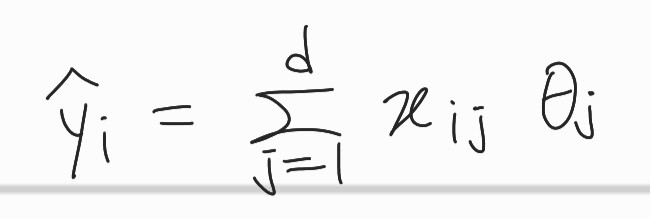
각 feature 마다 다 다른 가중치 를 부여한다. 지도학습으로 x에 대해 y target값을 구하는 선형적인 모델을 구하는 것이다.
학습시: → learner → 수정
test시: → predictor →
학습시, x input과 그 input에 맞는 정답값 y를 모델에 학습시켜 다른 새로운 x값이 input으로 들어왔을때, 알맞은 y값을 예측할 수 있도록 값을 update하는 것이다.
loss function
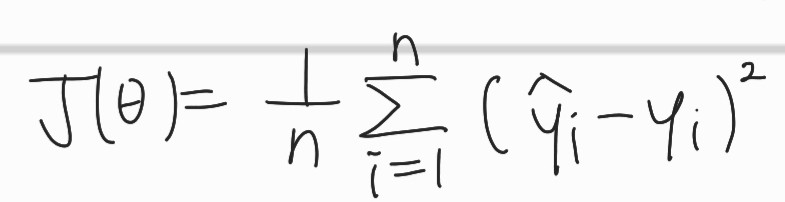
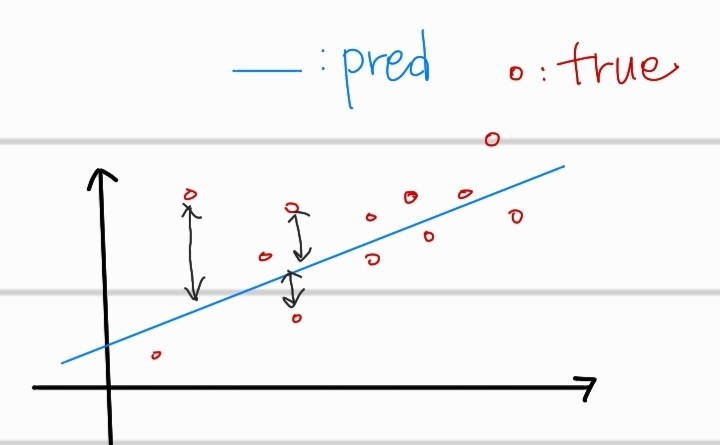
이는 target값과 predict값의 차이에 대한 loss함수 이다. 쉽게 예측값과 원래 정답인 값 사이의 오차를 계산하는데 음의 부호를 없애기 위해, 제곱을 취한 것 뿐이다. 또한, 절댓값을 취하는 것보다 좋은 이유는, 2차함수에 대한 미분도 편이하기 때문이다. 아무튼, 위의 식의 값을 최소화 하기 위해서 값을 update해야 한다. (x의 값을 수정할 수는 없음)
그렇다면 어떻게 를 수정해야 할까????
SGD(Stochastic Gradient Descent)
- Gradient Descent algorithm
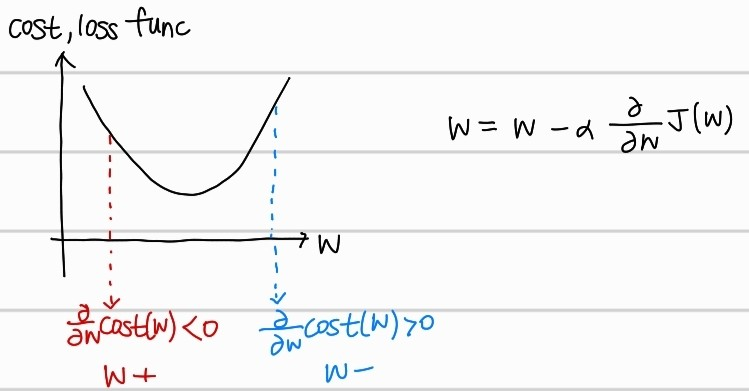
위의 cost 그래프를 보면, w의 값에 따라 기울기가 다름을 알 수 있다. w일때, cost 그래프에서의 기울기가 양수면 w를 감소시키고, w일대, cost 그래프에서의 기울기가 음수면 w를 증가시키는 방향으로 w를 update하는 것이다.이는 gradient descent algorithm의 큰 뼈대라고 할 수 있다.
수식에서의 는 learning rate로 얼마만큼 많이 w를 이동하는지를 조절해준다. 값이 크면 클수록 한번에 더많이 수정되는 것이다.
기본적으로 미분값을 토대로 w를 수정하는 것이다. 여기서 수정할때 보는 데이터의 크기로 다양하게 분류된다.
1) Batch Gradient Descent(BGD): 전체 데이터셋에 대해 error 구한뒤, 기울기 한번 계산 후 w 수정
2) Stochastic Gradient Descent(SGD): 임의의 하나의 데이터에 대해서 error구한 뒤, 기울 계산 후 w 수정
3) Mini-batch Gradient Descent(MGD): 전체 데이터셋 에서 mini-batch만큼 선정한 데이터에 대해서 기울기 계산후 그 평균기울기로 w 수정
여기서 batch라는 생소한 개념이 나왔는데 한번 잡고 가자.
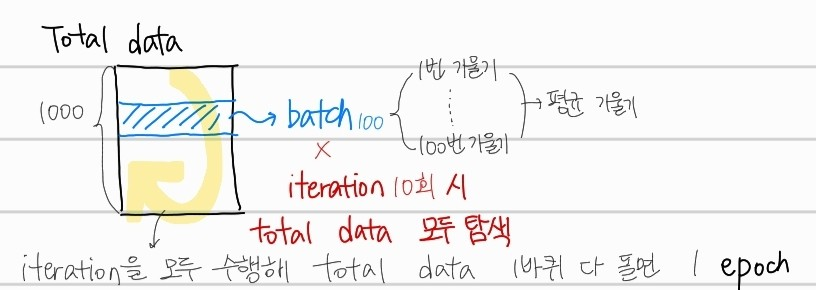
batch size만큼의 데이터를 total data에서 뽑아낸 뒤, 평균 기울기를 구하여 w를 수정한다. 이를 total data를 모두 사용할때까지 반복하게 되는데, 이 반복 횟수를 iteration이라 하고, 한번 total data를 모두 탐색하면 1epoch이라고 한다.
아쉽게도 모든 loss function이 2차함수의 꼴은 아니다. 실제로 다양한 결과값에 대해 예측한 값과의 차이를 비교하게 되면, local minima가 생기는 형태이다. 여기서 일반적인 gradient descent알고리즘은, w를 수정하다가 이 작은 구덩이에 빠져 못나오게 되어서 global minima 즉 최종 목적지에 도달하지 못할 수 있다. 이때 해결책으로 Momentum을 부여하자는 방식이 등장했다.
SGD+Momentum
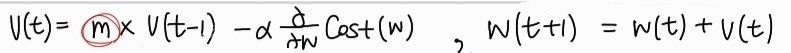
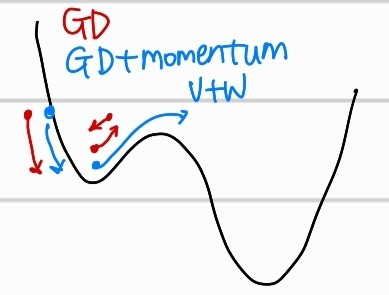
m은 관성계수로 0.9 정도의 값을 부여한다. 이전 미분값을 속도로 생각하고 활용해서, 이전 w의 위치가 경사진 곳이였다면 더 값이 커져서 속도가 붙듯이 더 많은 값만큼 w가 수정되어 local minima를 빠져나올 수 있는 방법이다. 여기서, local minima는 해결했지만, global minima에 도착하지못하고 이전 미분값에 영향을 받아 overshooting되는 상황이 생긴다. 즉 global minima에 도착하지못하고 계속 swing하게 되는 것이다. 이를 해결하기 위해서, 현재의 기울기에 대한 영향력을 키우기 위한 방법이 등장한다.
Adagrad(Adaptive Gradient Descent)

이 수식을 살펴보면, 현재 기울기 앖을 제곱해서 적용하는 것을 알 수 있다. G(t)의 값이 w 수정시 분모로 포함되어서, 최종적으로 기울기가 큰 상태일때 조금만 이동할 수 있게끔 w를 수정하는 것이다. 어느정도 overshooting을 해결하고 현재 기울기의 적용정도를 높일 수 있지만, 이때 가중치 변화율의 제곱을 사용하기 때문에, G값이 계속 누적해서 증가하는 점이 있다. 따라서, 아직 global minima에 도착하기 이전인데도, 누적도니 G값때문에 w에 대한 수정이 이뤄지지 않을 수 있다. 따라서, 이를 수정하기 위해서 이전 G값과 반영비율을 적용해서 G의 누적을 완화시킨 방법이 있다.
RMSprob

값을 활용해서, 이전 G값과 비율을 설정함으로써, G가 누적되어, 기울기와 연관없이 누적된 G때문에, w가 조금 수정되는 점을 수정하였다.
Adam
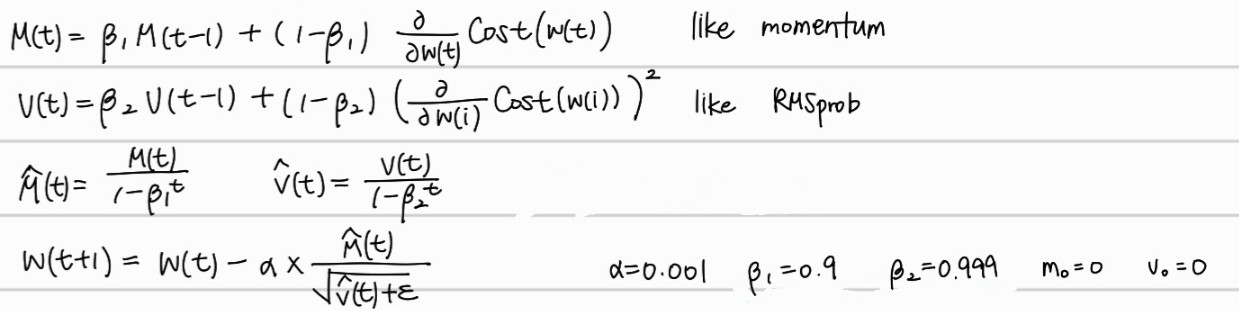
adam optimizer는 momentum과 adagrad 및 RMSprob을 합친 알고리즘으로, 속도에 대한 값과, 이전 G값과 현재 G값에 대한 비율 반영을 모두 적용한 알고리즘으로 딥러닝에서 가장 많이 사용되는(거의 이것만 사용하는) 알고리즘이다. 와 를 사용하는 이유는 학습 초기에 가중치가 너무 작게 반영되어서 계산될까봐, 초기 미분값을 작아지지 않게 반영할 수 있게 해준다.
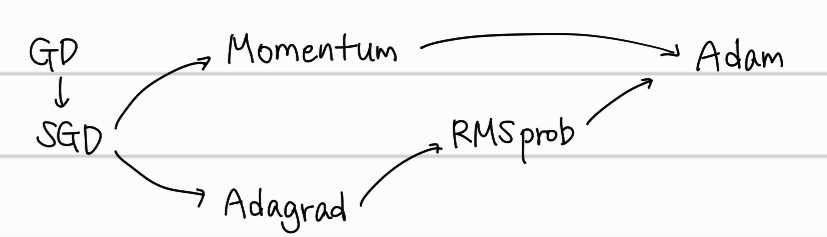
다음은 optimization의 다양한 종류에 대한 발전 과정을 단순하게 그려본 것이다.