지난 글에 이어 overfitting을 해소하기 위한 Batch normalization에 대해서 작성해보고자 한다. 먼저 정규화를 하는 이유와, Normalization, Standardization, Regularization 모두 정규화로 해석 되는데, 모두 다르다는 것을 짚고 넘어가자.

Normalization , Standardization , Regularization

위는 Normalization부터 Regularization까지 수식을 정리하고 간단한 특징이다.

Normalization

• 값의 범위를 0~1 사이로 바꿔주는 방법
• 특정 feature의 값이 너무 클때 해당 값이 학습에 주는 영향을 줄이는 효과
• 오버피팅을 방지해줌

Standardization

• 값의 범위를 $\mu$=0 $\sigma^2$=1 로 바꿔주는 방법
• 정규분포를 표준정규분포로 변환하는 것과 동일함
• 오버피팅을 방지해줌

Regularization

• Loss함수에 weight의 절댓값(Lasso)나 제곱(Ridge)를 더해줘 특정 weight가 영향을 많이 주는 모델이 되지않게 만들어줌 → 네트워크에서 weight의 분포가 고르게 규제하는 방법
• 오버피팅을 방지해줌

---

위의 방법들 모두, 특정 feature가 학습과정에서 큰 영향을 주지 못하게 억제하는 방법인데, 이는 오버피팅을 막기 위해서이다. 학습하는 과정에서 특정 feature의 weight가 커지게 되면, 훈련 데이터에 대해서 너무 과적합된 모델이 된다.

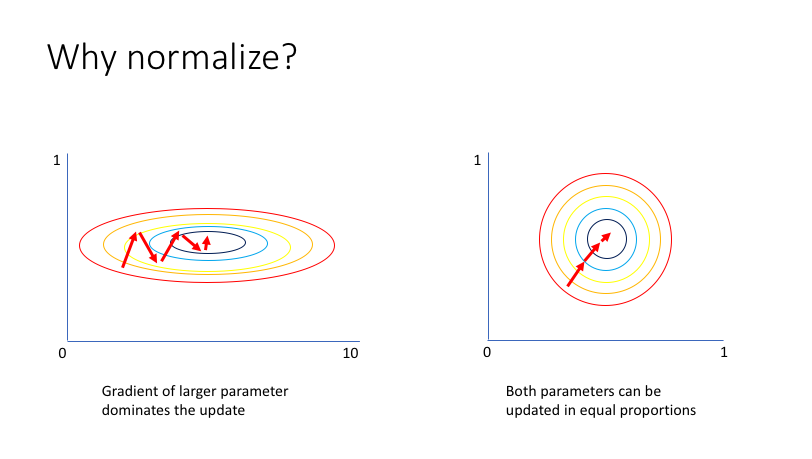
위의 좌측 case를 보면 x축의 feature가 너무 크기 때문에 x축을 위주로 파라미터가 갱신되어 y축 방향의 feature가 상대적으로 무시되어 오른쪽의 정규화된 case보다 비효율적으로 최적화 과정을 거치게 된다.

Feature 간 값의 범위를 조정하여 효율적으로 학습하도록 설계하여도, 딥러닝의 경우 layer를 통과할때마다 각각 출력값의 데이터 분포가 다르게 나타나는 현상이 있다. 이를 Internal Covariate Shift 현상이라고 한다.

Internal Covariate Shift(ICS) 내부 공변량 변화

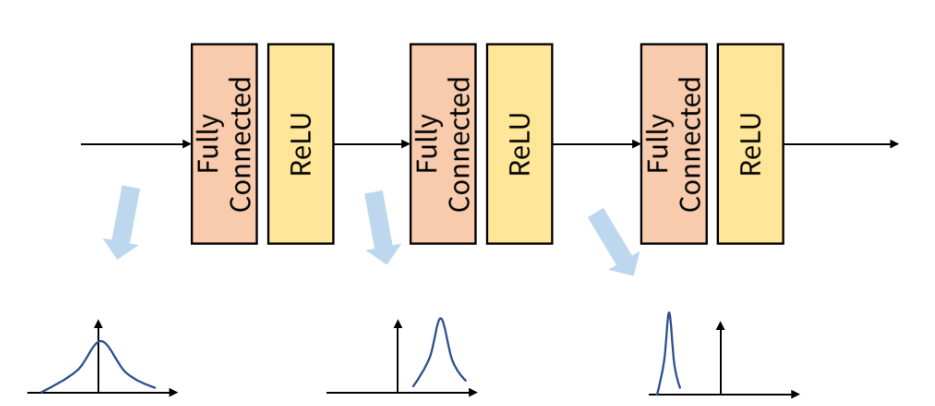
위의 그림과 같이 매 layer마다 다른 형태의 표준정규분포곡선을 보인다. 이처럼 한개의 Batch를 대상으로 layer를 지날때마다 layer간 차이가 있을 수 있지만, Batch 간에서도 이 현상은 발생한다.

  Mini Batch SGD에서 특히 문제가 발생할 수 있다. 이렇게 배치마다, layer를 통과할때마다 각각 다른 output이 나오게 되면, 하나의 learning rate를 설정하기 어렵다. 너무 작은 learning rate를 설정하게 되면 local minimum에 갇혀 update되지 않고 학습이 종료 될 수 있다. 혹은 weight initialization을 생각해볼 수 있지만, 초기 가중치는 random으로 설정한뒤, backpropagation을 통해 학습해 나가는 것이 더 효율적이다. 따라서 Batch normalization을 수행하는 것이다.

Batch normalization

Batch Normalization은 Batch 별 평균과 분산을 이용해서 Normalization을 해 Internal Covariate Shift 현상을 완화시키는 것이다.

Training 과정

Train 단계에선 위의 순서대로 진행된다. 먼저 배치의 크기에 맞는 평균, 분산을 계산해주고, 이를 활용해서 정규화를 진행한다. 여기서 $\varepsilon$은 분모가 0이 되어 값이 발산하는 것을 막아주기 위한 clipping이다. $\hat x_i$는 평균이 0이고 분산이 1인 분포를 따르게 된다. 여기서 $\gamma$ 와 $\beta$를 사용하여 scale shift를 진행 한 후에, 이를 activation function에 입력하는 것으로 진행한다.

최종적으로 Activation 함수에 Bias를 포함하지 않은 $Wx$값만 Batch normalization을 거친 후에 입력한다. 어차피, $\beta$값이 존재하기 때문에, Bias를 포함하지 않아도 된다.

여기서 $\gamma$와 $\beta$는 learning parameter 즉 학습하는 파라미터이고, 역할은 밑에 자세하게 다루겠다.

Testing 과정

Test하는 과정은 Training과정과 동일하게 진행할 수 없다. Trianing시엔, batch size에 맞게끔 모델에 입력하기 때문에 배치마다 평균이나 분산을 구할 수 있지만, Test시 32개씩 입력값을 넣고 test를 할 수는 없기 때문이다. 따라서, Test 과정에서는 Training시 계산했던 평균과 분산을 이용해서 진행한다.

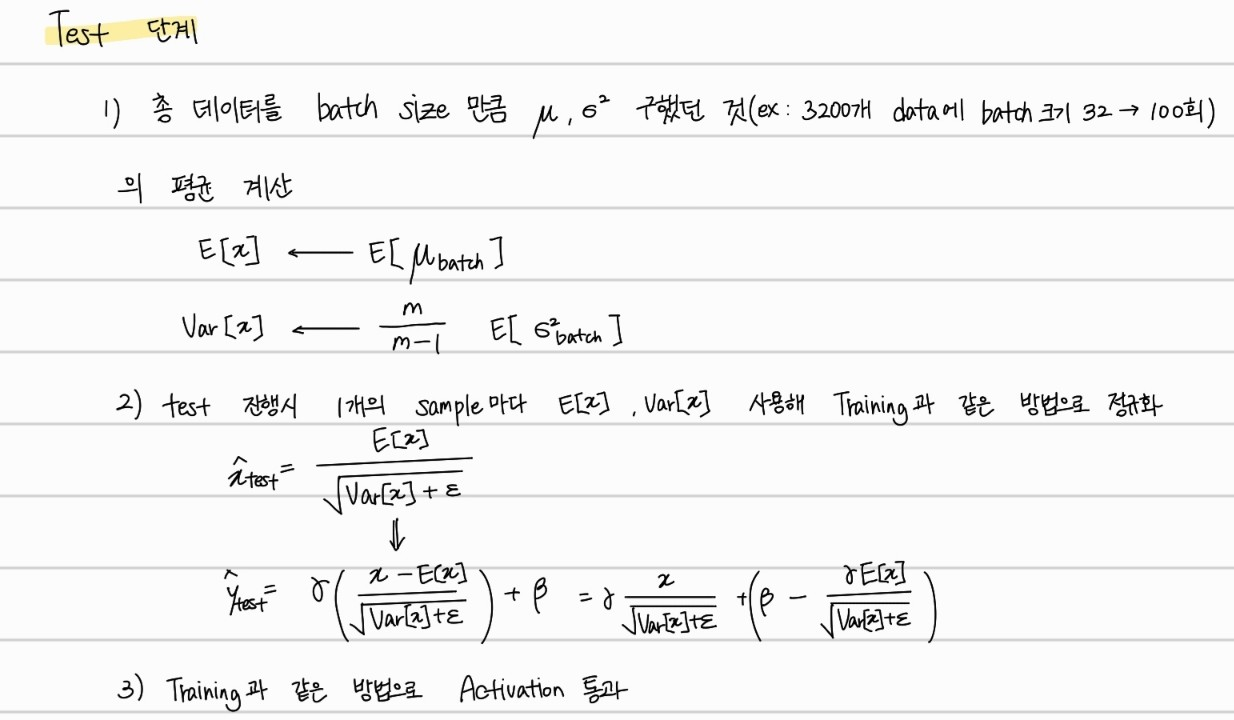
위의 방식대로, Train 과정에서 계산한 평균과 분산의 평균을 계산하여 이를 활용해 각 test sample마다 정규화 된 값으로 output을 가지게 진행한다. 여기서 의문점은, 학습 초기의 배치 평균과 학습이 어느정도 이뤄지고 난 후의 배치 평균은 다를 것이라는 점이다. 학습 초기의 배치 값들은 초기화된 값에서 크게 바뀌지 않아 불필요한 값들이 존재할 가능성이 높다 이에 대해서도 밑에 자세하게 다루겠다.

분산의 평균을 구할 시 $\frac m {m-1}$을 곱한 이유

Training 과정에서 계산한 분산에 대한 평균을 구하면 이는 $\frac {m-1} m$ 이라는 bias값을 가지게 된다. 따라서, Training 과정에서 얻은 분산에 대한 평균을 구했을때 모분산(전체 데이터 셋)에 대한 분산을 얻을 수 있게 하기 위해서 곱해준 것이다.

Batch 평균과 분산의 평균 사용시 학습 초기값시 garbage 값 control

Exponential moving average를 사용하여 여러 Batch 평균과 분산 중 학습 초기에 얻은 값들은 최대한 잊어가면서 평균을 구하는 방법을 사용한다.
Exponential moving average에 대한 설명 포스트

$\gamma,\beta$의 직관적이 이해

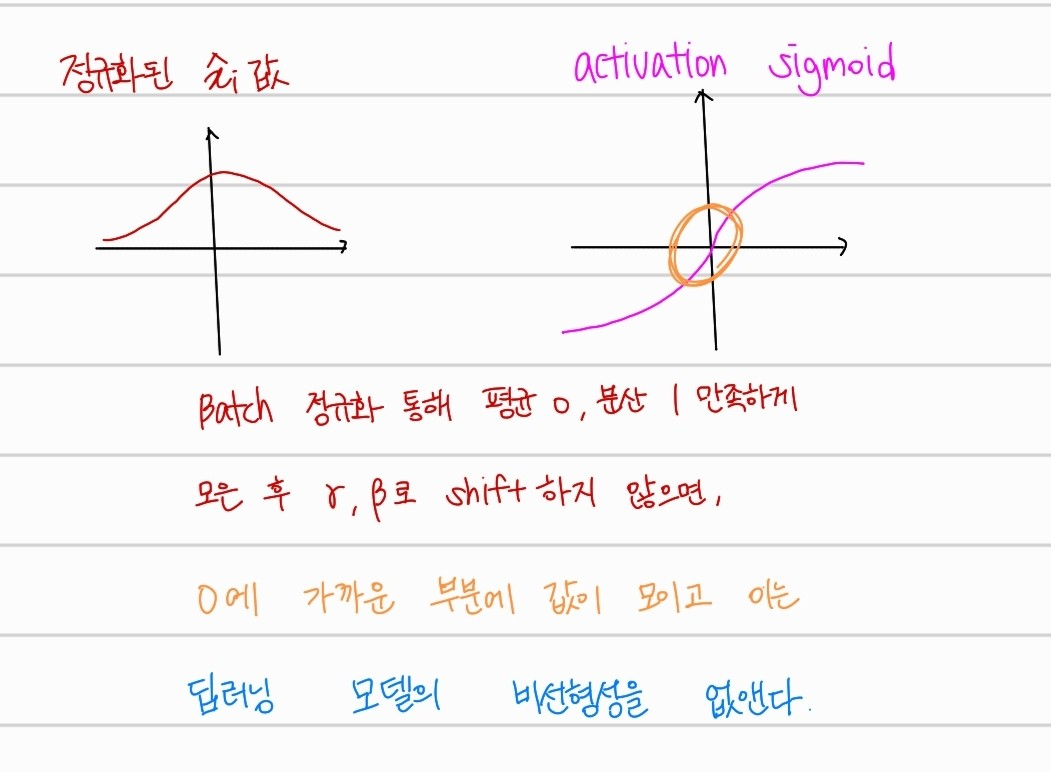
위의 그림과 같이, 정규화한 값들을 $\gamma,\beta$로 다시 shift하지 않는다면, layer를 지나는 모든 배치의 값들이 0에 가까운 곳에 위치하게 된다. 이는, 딥러닝에서 제일 중요한 비선형성을 잃게 만드는 것이다. 따라서, learning parameter로 $\gamma,\beta$ 를 설정해 비선형성을 유지하면서, 배치간 Internal Covariant Shift 현상을 극복하는 method이다.

---

Reference

https://heytech.tistory.com/438
https://www.youtube.com/watch?v=m61OSJfxL0U