NN <4> Bias, Variance trade off 및 오버피팅(1)

김동한·2024년 6월 13일

Nerual Network

목록 보기

5/10

Overfitting

딥러닝은 결국 모델이 실제 값 $y$ 와 차이 (loss) 가 최소화되는 값 $\hat y$ 을 예측하게끔, 즉 올바른 값을 예측하도록 neuron의 weight 값을 update하는 것이다.
머신러닝과 다르게 train data의 feature,pattern등을 딥러닝 모델이 직접 알아간다. 이때, train data의 loss를 너무 작아지게끔 weight가 update되면 train data에만 맞는 모델이 된다. 즉, 새로 들어오는 test data에 대해 제대로 된 값을 예측하지 못하게 된다. 이를 overfitting 이라고 한다. overfitting에 대해서 자세하게 알기 위해서 bias와 variance에 대해서 알아보자.

Bias,Variance

$Bias[\hat y]=E[\hat y-y]$
$Var[\hat y]=E[(\hat y-y)^2]=E[\hat y^2]-E[ y]^2$

Bias는 모델이 예측한 값과 실제 값의 차이의 평균을 나타낸다. 즉, Bias값이 크면 모델이 예측한값이 실제 값과 차이가 큰 값이라는 것이다. Variance는 예측값이 어느정도로 다양하게 변화할 수 있는지를 나타낸다. 모델이 예측한 값이 얼만큼 퍼져서 다양한 데이터셋에 대해 예측가능한지 정도이다. Bias와 Variance는 실제로 trade off관계에 있다. 아래의 그림을 통해서 쉽게 알아보자

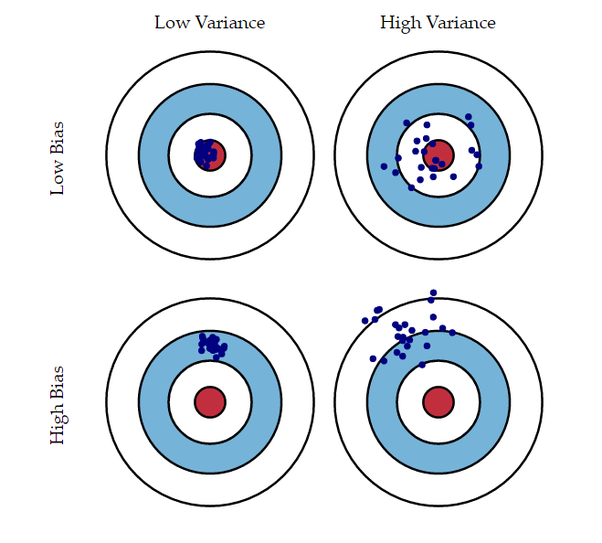위의 그림에서 빨간색 원은 정답의 위치이다. Bias가 작고 Variance가 높은 경우는 overfitting된 경우, Bias가 크고 Variance가 낮은 경우는 underfitting된 경우이다. 그러면, Bias가 작고 Variance도 작으면 괜찮은거 아닌가? 라는 생각을 할 수 있지만, 사실 저 case는 불가능하다. 아래의 그래프를 보자.

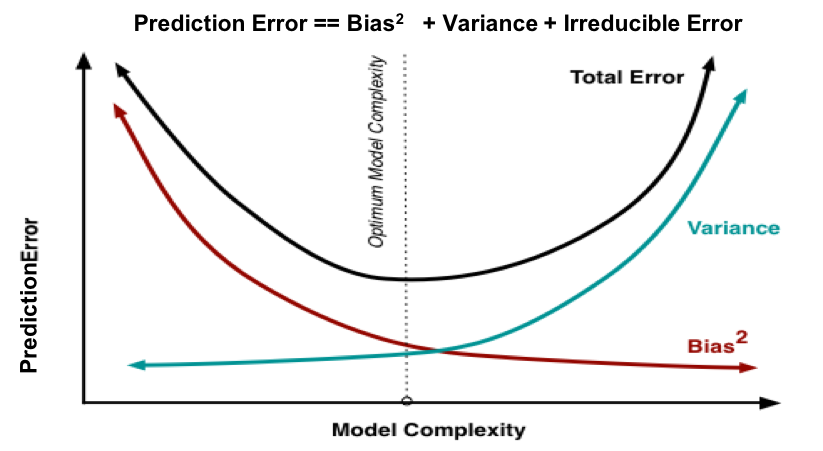이 그래프는 model의 complexity와 Bias,Variance의 관계를 나타낸다. complexity가 클수록 Bias는 작아지고 Variance는 높아지는 것을 알 수 있다. 사실 당연한 이야기이다. model이 복잡할수록, 더 train data에 대해서 잘 학습하게 된다. 무조건 잘 학습된다고 좋지않다. 너무 잘 학습하게 되기 때문이다.
다양한 noise가 존재하는 train data에 너무 잘 학습하게 되고, 즉 train data에 대해 많이 퍼지는 예측값을 예측하게 되는 것이다. 그리고 train target값과 train predict값의 차이는 즉 예측이 틀린 정도는 무조건적으로 작아질 수 밖에없고 이는 Bias가 감소한다는 것을 의미한다.

즉, 어느정도 Bias ( $E[\hat y-y]$ )가 있는 상태의 모델. 즉 train data에 대해 적당히 복잡한 모델이어야 오히려 과적합되지않는 것이다. 아래로 정리할 수 있다.

Bias가 크고 Variance가 낮은 경우 → underfitting (모델이 너무 단순함 → train data도 학습 잘 못함)

Bias가 작고 Variance가 큰 경우 → overfitting (모델이 너무 복잡함 → train data에 정교하게 학습함)

간단한 classification의 예시로 그래프를 보자.

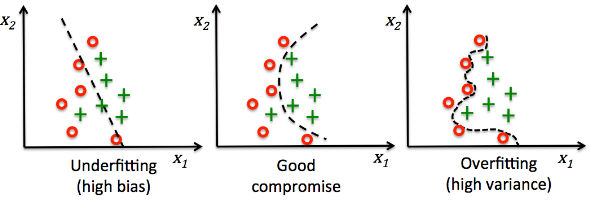
첫번째 예시는 너무 구분을 못하고 마지막 예시는 너무 상세하게 구분해서 새로운 데이터에 좋은 성능을 내지 못한다. 따라서 적당한 Bias와 Variance를 갖는 모델을 구축하는 것이 목표이다. 이렇게 overfitting 되는 상황을 해결하기 위해 다양한 방법이 있다.

Regularization

모델이 너무 train data에 잘 학습하지않게끔, Loss 함수에 규제 함수(Regularization term)을 추가해 학습시 손실함수가 너무 작아져서 overfitting되는 것을 방지하는 기법으로 특정 weight에 너무 의존하지않고, 균등하게 weight를 반영할 수 있게끔 weight에 penalty를 주는 방법이다.

L1(Lasso), L2(Ridge) Regularization

먼저, 두 정규화의 차이를 알기 위해 Norm에 대해 짚고 넘어가자. Norm은 유한한 벡터 공간에서 벡터간 거리, 벡터의 절대적인 크기(Magnitude)를 나타낸다.

$L_p=(\sum_i^n|x_i|^p)^\frac 1 p$

p=1 → L1 norm , p=2 → L2 norm 을 의미한다. n은 벡터의 요소 갯수를 의미한다. Norm의 계산 결과는 원점에서 벡터 좌표까지의 거리 (Magnitude)를 의미하고, 이 L1,L2 norm값을 loss function에 더해줌으로써 penalty를 부여하는 것이다.

L1 norm (Manhattan distance)

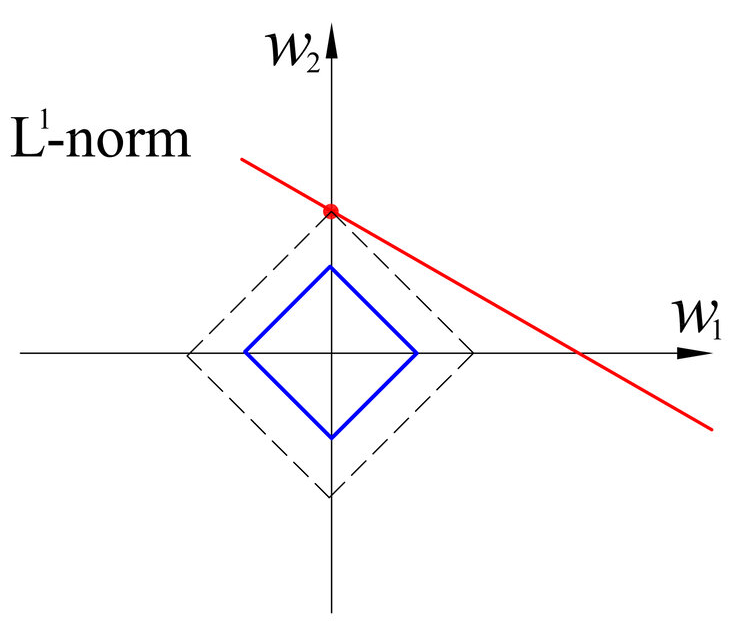특정 방향으로 움직일 수 있는 조건이 있다면 두 벡터간 최단 거리를 찾는데 사용된다. 실제 값과 예측한 값 오차들의 절댓값에 대한 합 ( $L_1=\sum_i^n|y_i-\hat y_i|$ ) 으로 나타낸다.

L2 norm (Euclidean distance)

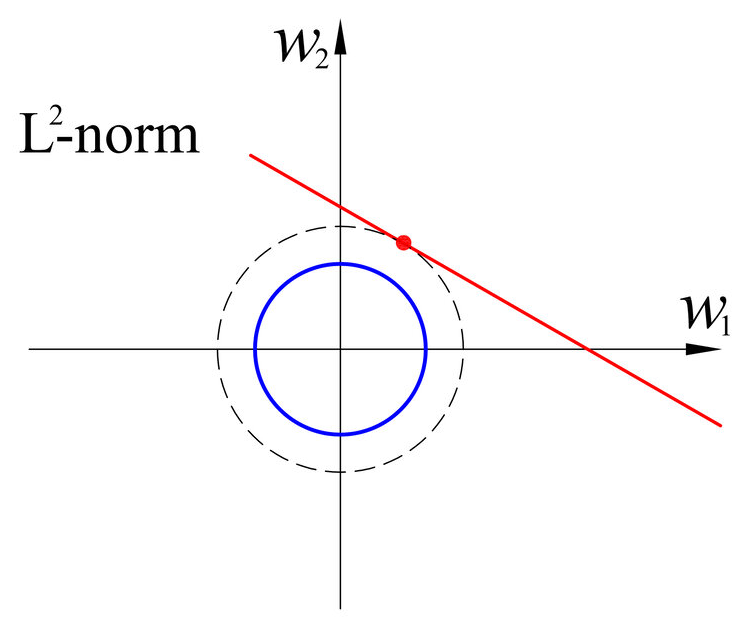두점사이의 최단 거리를 측정할때 사용된다. 우리가 흔히 아는 오차의 제곱합이다. 실제 값과 예측한 값 오차들의 제곱의 합( $L=\sum_i^n(y_i-\hat y_i)^2$ )으로 나타낸다.

L1 Regularization

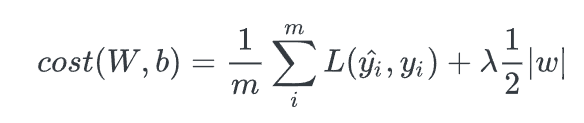
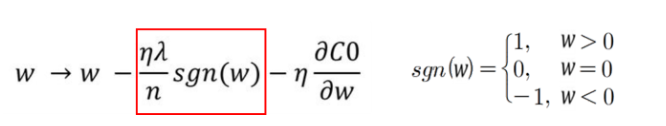
L1 regularization은 loss function에서 가중치의 절댓값의 합을 더하는 형태이기 때문에 미분했을 때의 weight의 크게 상관없이 부호로 상수값을 빼거나 더해주기 때문에, 특정 weight을 0으로 만들 수 있다. 즉 feature selection이 가능하다. 특정 weight만 사용할 수 있다.
또, 오차의 절대값을 사용해서 L2 보다 outlier에 더 강인하다. 하지만, 0에서 미분이 불가능하다. gradient를 기반으로 하는 학습(Gradient Descent) 에서 이 점을 유의해야하고, 편미분을 하게 되면, weight의 부호만 남아 weight의 크기가 커진다고해서 규제값이 커지는게 아니기 때문에 Regularization하는 효과가 L2보다 덜하다.

L2 Regularization

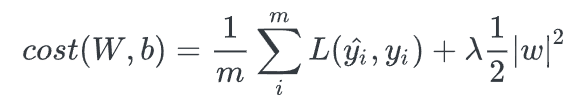
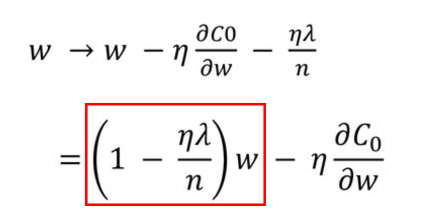
L2 regularization은 loss function에서 가중치의 제곱의 합을 더해주는 형태라서 weight의 크기에 따라 weight값이 큰 값을 더 빠르게 감소 시키는 weight decay기법이다. weight의 크기에 따라 페널티의 정도가 바뀌는 L2는 L1보다 더 효과가 좋다. $\lambda$ 를 통해서 규제하는 정도를 조절가능하다. outlier에 대해 L1보다 더 민감하게 반응하지만, weight의 크기만큼 페널티를 줄 수 있어 일반적으로 더 좋은 학습 효과를 얻는다.

간단한 예시일 수 있지만, 위의 사진에서는 $w_2$ 이 $w_1$ 보다 더 균등하게 가중치가 분포한 더 옳은 예시임을 알 수 있다. 이를 L1 규제를 계산해보고, L2 규제를 계산해보았을때 loss function에 더해지는 값을 위와 같이 계산 할 수 있다. L1 규제를 사용했을 때 둘의 차이를 내지 못한 반면, L2 규제에선 $w_2$ 가 더 올바른 weight 분포임을 알게 해준다.