RNN gradient exploding/vanishing

김동한·2024년 9월 1일

NLP

목록 보기

10/21

RNN에서의 gradient vanishing, exploding 문제를 한번 수학적으로 파악해보자.

먼저, 간단한 예시로 확인해보기 위해서 RNN에서 사용되는 weight matrix를 모두, scalar로 가정하고 접근해보았다.

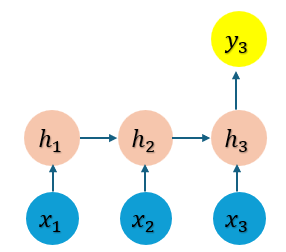
위와 같은 RNN에서 $x_3$ 까지의 input에 대한 backpropagation 과정을 진행해보자.

먼저 위의 RNN에 대한 수식을 간단하게 아래와 같이 정리해보았다.

h_1=\text{tanh}(ah_0+bx_1+c)\newline h_2=\text{tanh}(ah_1+bx_2+c)\newline h_3=\text{tanh}(ah_2+bx_3+c)\newline y_3=dh_3+e

위는 feed forwarding 즉 순전파에 해당하는 수식이다. 그냥 간단하게 이전 hidden state에 a를 곱하고, input에 b를 곱해 더하고, bias c를 추가한 것이다.

여기서, $\frac {df} {dh_1}$ 를 구해보자. 이는, 첫번째 hidden state에서의 gradient을 의미한다.

backpropagation 과정에서는 합성함수의 미분이 이뤄진다. 따라서, $\frac {df} {dh_1}$ 는 아래와 같다.

\frac {df} {dh_1}=\frac {dh_2} {dh_1} \times \frac {dh_3} {dh_2} \times \frac {dhf} {dh_3}

위의 수식의 우변에 해당하는 각 항들은 좌측부터 차례로, $h_2$ 를 $h_1$ 으로 미분한 gradient 부터 최종 output 함수에 해당하는 $f$ 를 $h_3$ 으로 미분한 gradient이다.

차례로 각각 어떤 값인지 계산해보자. 먼저,

$\frac {dhf} {dh_3}=d$

$y_3$ 를 구하는 수식을 $h_3$ 로 미분한 것이기 때문에 쉽게 d인것을 알 수 있다. 그다음으로,

$\frac {dh_3} {dh_2}\leq a\times1$

마지막으로 첫번째 항의 미분 값도 계산해보면, 같은 값을 가지는 것을 알 수 있다.

$\frac {dh_2} {dh_1}\leq a\times1$

최종적으로 $\frac {df} {dh_1}$ 은 아래와 같이 부등식으로 표현할 수 있다.

\frac {df} {dh_1}\leq a\times1\times a\times1\times d

즉, hidden state의 수 만큼, a가 곱해지는 것을 알 수 있다. 따라서, a가 1보다 크다면 gradient exploding, 1보다 작다면 vanishing 문제가 발생하게 된다.

원래로 돌아와 RNN의 $h_t$ 의 수식은 아래와 같다.

h_t=\text {tanh} (W_{hh}h_{t-1}+W_{xh}x_t+b)

$h_t$ 는 최초의 hidden state vector에 hidden state를 연결하는 weight matrix를 반복으로 곱하는 것과 유사하다. 즉, 아래와 같이 표현할 수 있다.

h_t\propto W_{hh}^{t-1}h_1

이때, $W_{hh}$ 가 eigen decomposition을 통해 $VDV^{-1}$ 로 분해될 수 있다고 가정하면, D는 Eigen value의 대각행렬로, Eigen value의 지수승을 곱하게 된다.

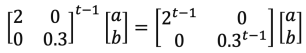
가중치 행렬 $W_{hh}$ 를 Eigen decomposition 했을 때, Eigen value의 절대값이 1보다 크면 exploding, 보다 작으면 vanishing이 일어난다는 것을 알 수 있다.

tanh 미분

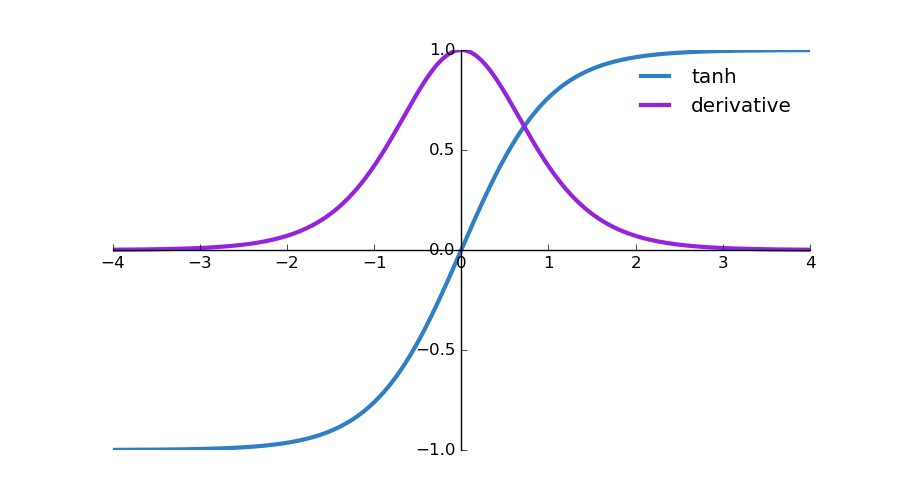
임을 알 수 있다 그 이유는 tanh의 미분은 최대로 나올 수 있는 값이 1이기 때문이다. 먼저, tanh 함수는 다음과 같다. $y = \tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}$ 위를 미분하게 되면, $\frac{dy}{dx} = \frac{(e^x + e^{-x})(e^x + e^{-x}) - (e^x - e^{-x})(e^x - e^{-x})}{(e^x + e^{-x})^2}$ 몫의 미분법에 의해 위와 같은 수식이 되고 이를 정리하면, $\frac{d}{dx} \tanh(x) = 1 - \tanh^2(x)$ 라는 미분값을 얻을 수 있다. 이 미분 결과의 최대값은 tanh가 0일때 1이다.

(●'◡'●)