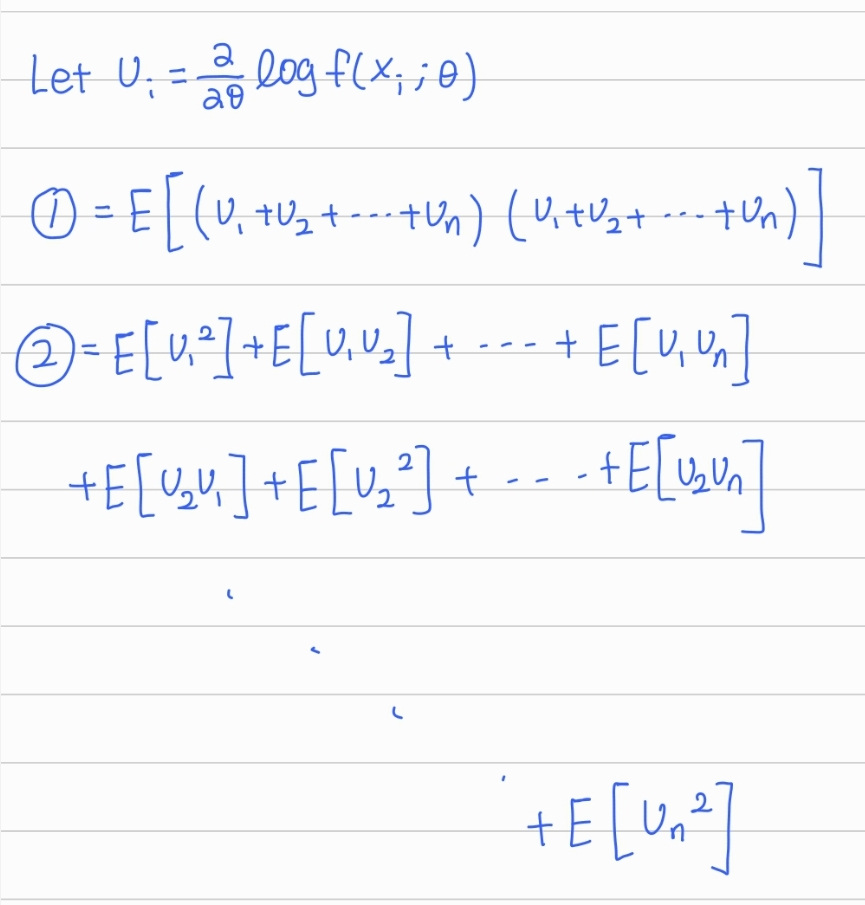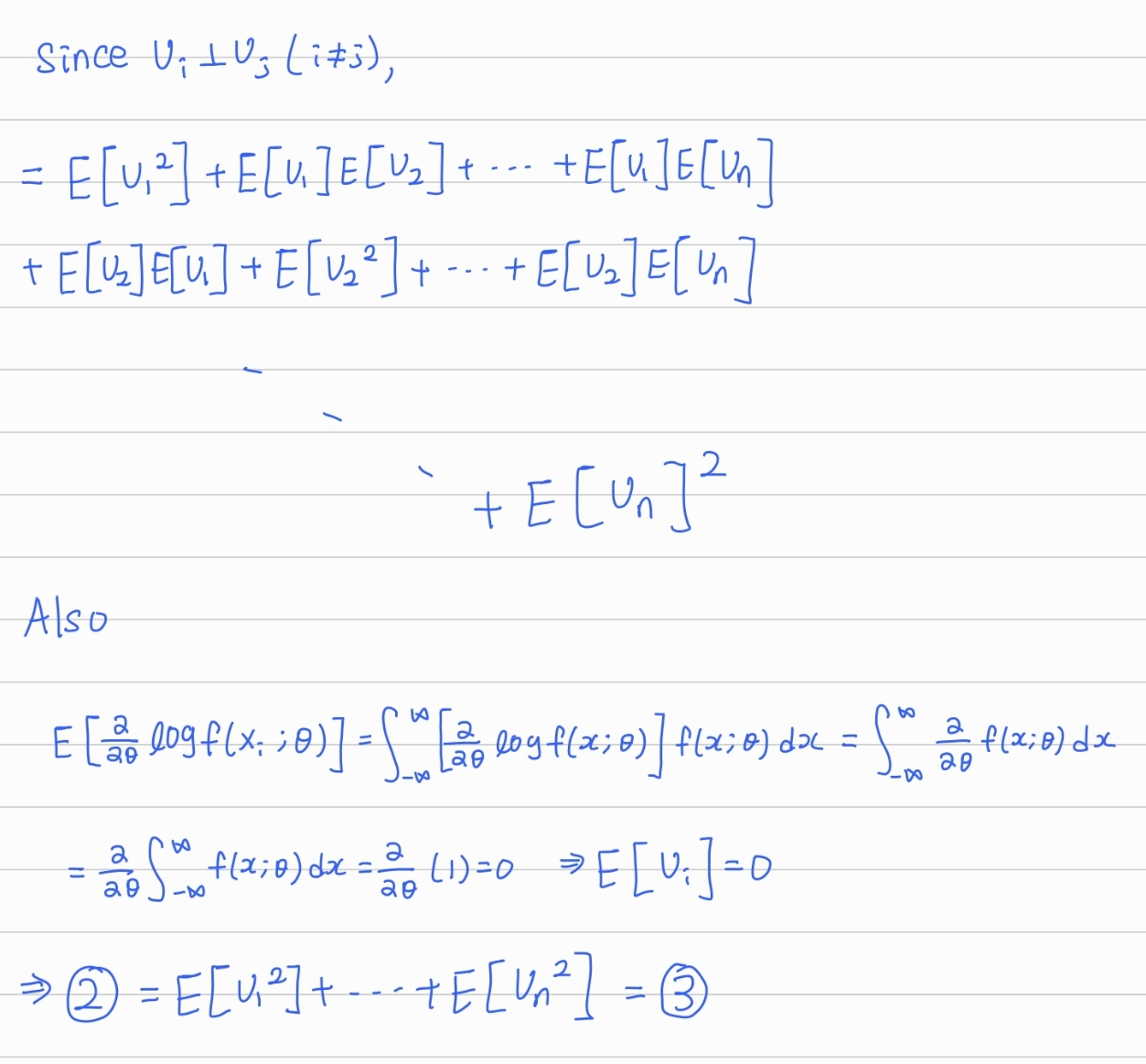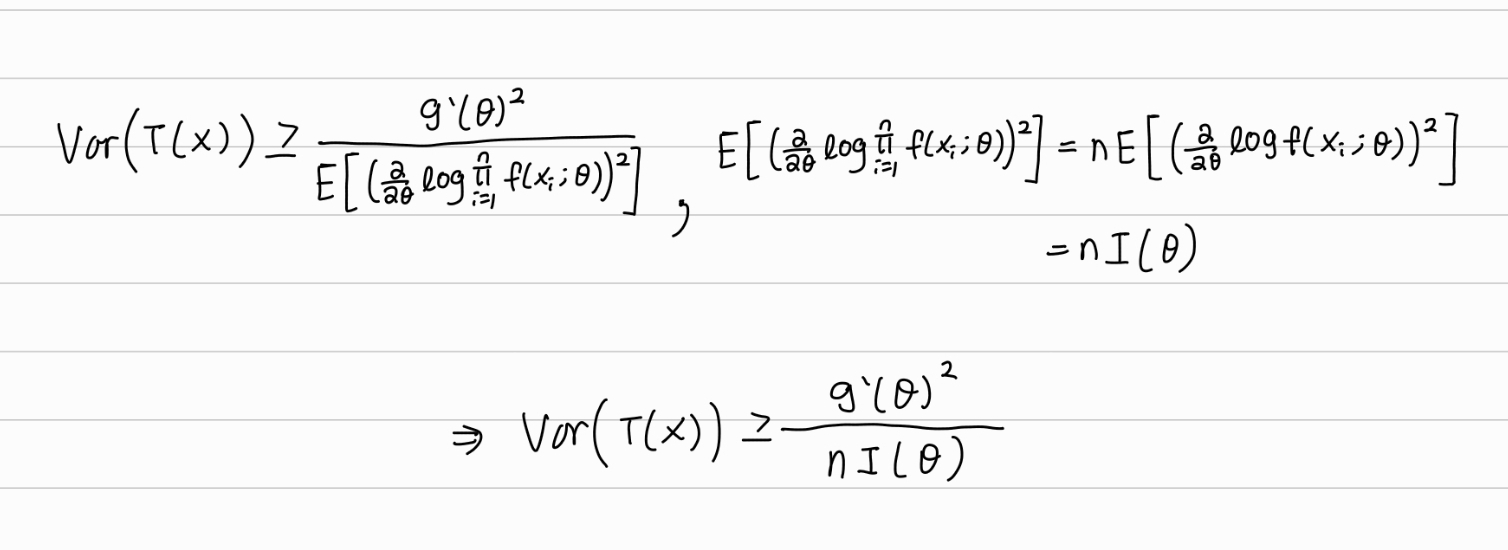MVUE, 크래머-라오 하한

MVUE

최소분산비편향추정량(MVUE)는 비편향추정량 중에서 분산이 가장 작은 추정량을 의미한다.

추정량의 모수와의 평균적인 거리를 나타내는 지표인 MSE는 다음과 같이 편향과 분산으로 분리 가능하다.

그런데 비편향추정량인 경우 bias는 0이 되므로 MSE는 추정량의 분산이 된다.
따라서 분산을 최소화하는 추정량을 찾으면, 추정량의 실현값들이 모수 근처에서 정밀하게 추출된다. 이 것이 MVUE를 찾으려는 이유이다.

MVUE
1. $E(T^*(X)) = \theta$
2. $\theta$에 대한 임의의 비편향추정량 $T(X)$에 대해 $Var(T^*(X)) \le Var(T(X))$

1.과 2.를 만족하는 $\theta$의 비편향추정량 $T^*(X)$가 존재하면 $T^*(X)$는 $\theta$의 MVUE다.

크래머-라오 하한

MVUE를 탐색하는 첫번째 방법은 크래머-라오 하한을 이용하는 것이다. 크래머-라오 하한은 비편향추정량의 분산이 가질 수 있는 하한값을 제시한다. 따라서 만약 비편향추정량의 분산이 하한값과 동일하다면 해당 추정량은 MVUE가 된다.

정칙조건

크래머-라오 하한을 도출할 때 가정하는 확률함수에 대한 몇가지 조건이 있다.

1. $\theta \neq \theta' \Rightarrow f(x;\theta) \neq f(x;\theta')$
2. $f$는 모든 $\theta \in \Omega$에 대해 동일한 서포트 $A= \{x|f(x;\theta) > 0\}$를 가진다.
3. 모든 $x \in A, \theta < \Omega$에 대해 $logf(x;\theta)$는 두번 미분 가능하고, 도함수가 연속이다.
4. $T(X)$가 모든 $\theta \in \Omega$에 대해 $E(T(X)) < \infin$이면, 다음을 만족한다.

$\frac{\partial}{\partial \theta}\int_{-\infin}^{\infin} \cdots \int_{-\infin}^{\infin} T(x_1, ..., x_n) \prod_{i=1}^n f(x_i;\theta)dx_1 \cdots dx_n \\ = \int_{-\infin}^{\infin} \cdots \int_{-\infin}^{\infin} T(x_1, ..., x_n) \left[\frac{\partial}{\partial \theta}\prod_{i=1}^n f(x_i;\theta)\right]dx_1 \cdots dx_n$

다음은 크래머-라오 하한의 결과의 증명이다.

모든 $\theta \in \Omega$에 대해 $Var(T(X)) < \infin, E(T(X)) = g(\theta), 0 < I(\theta) < \infin$이면, $g(\theta)$는 미분가능하고

$Var(T(X)) \ge \frac{g'(\theta)^2}{nI(\theta)}$

를 만족한다.

증명)

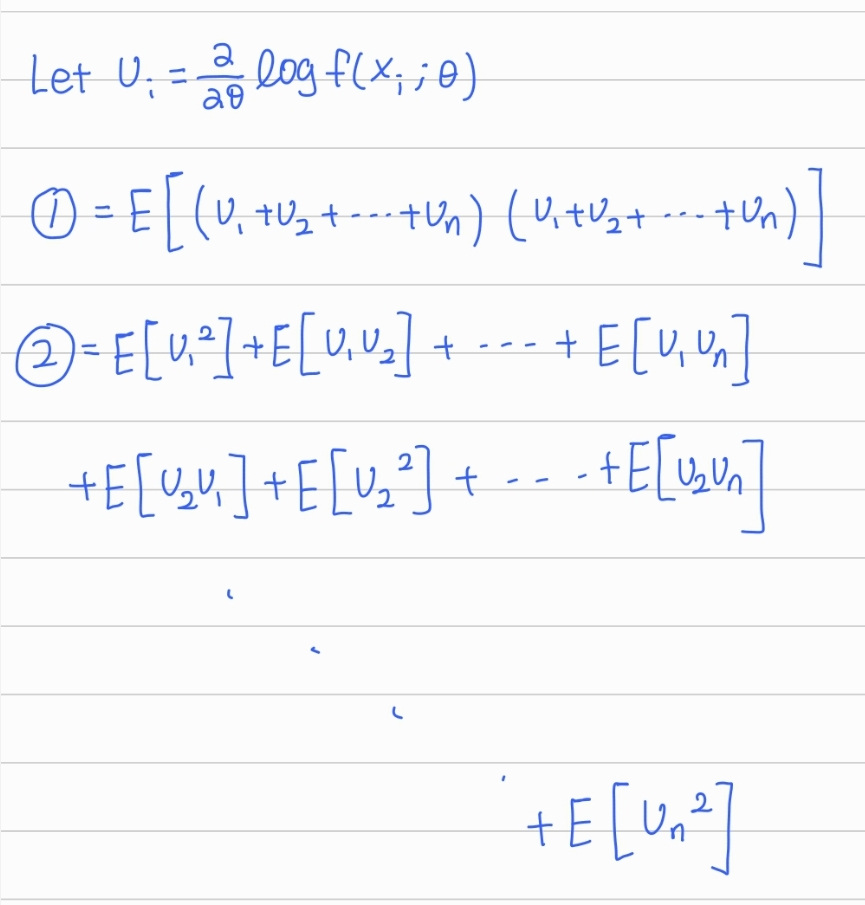
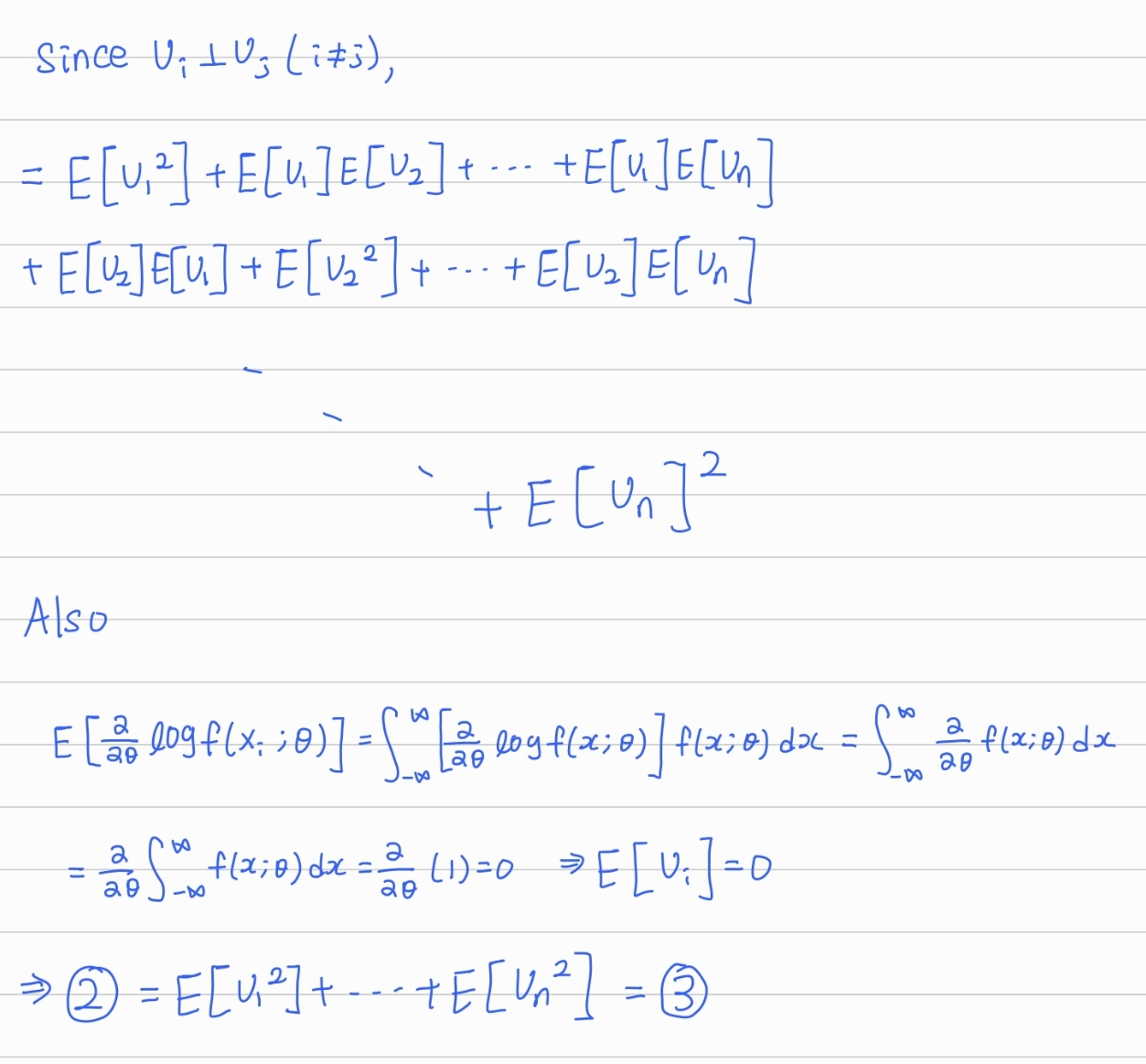
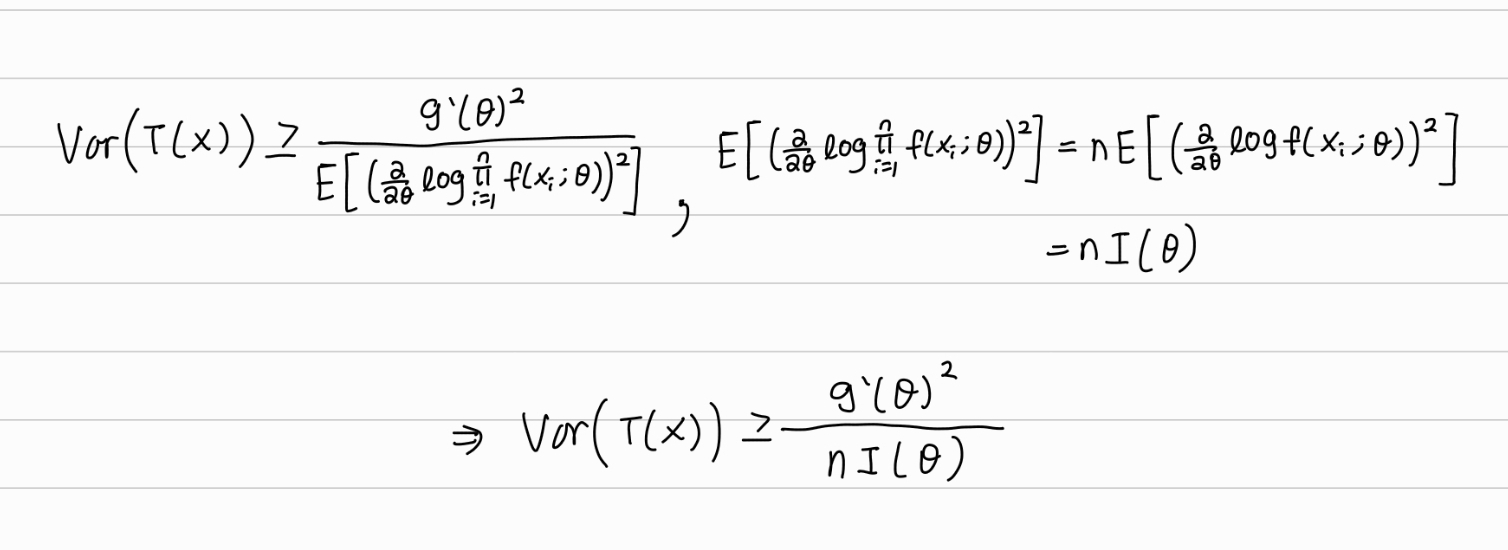
크래머-라오 하한을 이용한 MVUE 탐색의 한계점

1. 추정량의 분산이 꼭 크래머-라오 하한이 아니어도 MVUE가 될 수 있다. 크래머-라오 하한은 추정량의 분산의 하한을 제공할 뿐, 최소값을 제공하는 것이 아니다.

2. 정칙조건이 위반되는 겨우 크래머-라오 하한보다 더 작은 분산을 가지는 비편향추정량도 존재할 수 있다.