피셔 정보량의 직관적인 이해

STATS·2023년 8월 13일

목록 보기

37/40

피셔 정보량

피셔 정보량의 정의는 다음과 같다.

I(\theta) = E \left[\{\frac{\partial}{\partial \theta} log f(X ; \theta)\}^2\right]

피셔 정보량은 흔히 "표본이 모수를 추정하는데 얼마나 많은 정보를 주는가?"라는 뜻이라고 한다. 그런데 이 표현은 너무 추상적이다. "정보"란 무엇인가? "정보의 양"은 무슨 뜻인가?

이를 이해하기 위해서는 피셔 정보량의 함의를 살펴야 한다.

바틀렛 항등식

피셔 정보량의 뜻을 더 자세히 파헤치기 위해 바틀렛 항등식이라는 정의를 도입하자. 바틀렛 항등식의 성립조건이나 증명은 이 글에서는 중심 내용이 아니므로 생략하겠다.

1. E\left[\frac{\partial}{\partial \theta} logf(X ; \theta)\right] = 0 \\ {} \\ 2. E \left[\frac{\partial^2}{\partial \theta^2} logf(X;\theta) \right] + Var\left[\frac{\partial}{\partial \theta} logf(X;\theta)\right] = 0

피셔 통계량이 함의하는 것

이제 바틀렛 항등식을 이용해 피셔 통계량을 다르게 정의하자.

I(\theta) = E \left[\{\frac{\partial}{\partial \theta} log f(X ; \theta)\}^2\right] = E \left[\{\frac{\partial}{\partial \theta} log f(X ; \theta)\}^2\right] -0^2 = \\{} \\ E \left[\{\frac{\partial}{\partial \theta} log f(X ; \theta)\}^2\right]- E\left[\frac{\partial}{\partial \theta} logf(X ; \theta)\right]^2 = Var\left[\frac{\partial}{\partial \theta} logf(X;\theta)\right]

따라서 피셔 통계량은 로그-우도 함수( $l(\theta)$ )의 도함수의 분산임을 알 수 있다.

여기서 한가지 더 문제가 발생한다 : 로그-우도 함수의 도함수는 뭐고 도함수의 분산은 무엇을 의미하는가? 먼저 그 분포부터 살펴보자.

로그 우도 함수의 도함수 : 확률변수?

먼저 드는 의문은 로그 우도 함수는 $\theta$ 에 대한 함수인데 어떻게 확률 분포를 가지는가?이다.
이를 이해하기 위해서 앞으로 우리가 사용할 가정을 먼저 설정하자.

확률변수 $X$ 는 $N(0, 1)$ , $Y$ 는 $N(0, 25)$ 을 따른다고 하자. 그런데 각각의 모평균을 모른다고 가정하고, $X \sim N(\theta_1, 1)$ 이고, $Y \sim N(\theta_2, 25)$ 일 때 $\theta_1$ 과 $\theta_2$ 를 각각 추정하려 한다. 표본의 크기는 두 경우 모두 1000이라고 하자.

그렇다면 각각의 로그 우도 함수의 도함수는 다음과 같이 주어진다.

\frac{\partial}{\partial \theta}l_{\theta_1}(\theta) = \left(\sum_{i=1}^n X_i\right)-1000\theta \\ {} \\ \frac{\partial}{\partial \theta}l_{\theta_2}(\theta) = \left(\frac{1}{25}\sum_{i=1}^n X_i\right)-40\theta

따라서 로그 우도 함수의 도함수는 표본 $\{X_1, ..., X_n\}$ 에 대한 함수임을 알 수 있다. 따라서 로그 우도 함수의 도함수의 확률 분포는 어떤 고정/가정된 $\theta$ 에 대한 확률 분포를 의미한다.

로그 우도 함수의 도함수의 확률 분포

이제 로그 우도 함수의 도함수의 확률 분포를 직접 살펴보자.

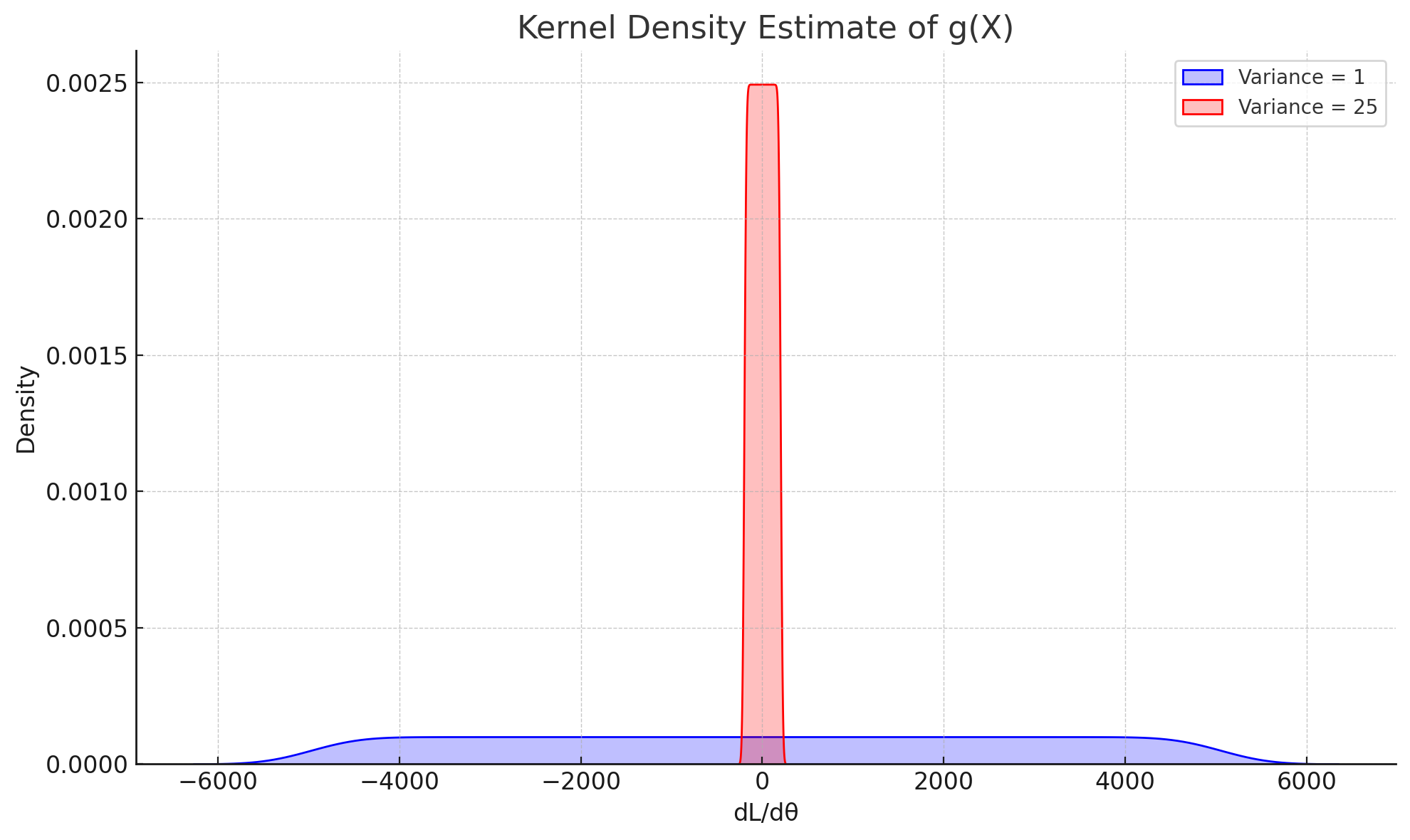
각각은 $\frac{\partial}{\partial \theta} l(\theta)$ 의 확률분포를 나타낸다.
$\sigma^2 = 1$ 의 $dl/d\theta$ 의 분포가 $\sigma^2 = 25$ 의 $dl/d\theta$ 의 분포보다 분산이 훨씬 큰 것을 알 수 있다. 피셔 정보량을 정의했던 것을 떠올리면 $\sigma^2 = 1$ 의 경우가 피셔 정보량이 크고, $\sigma^2 = 25$ 의 경우가 피셔 정보량이 작다.

분산이 크다는 것은 확률 변수가 가지는 값이 평균에서 멀리 떨어진 곳에서도 자주 추출된다는 것이다. 따라서 $\sigma^2 = 1$ 의 경우 $\sigma^2 = 25$ 에 비해 극단적인(평균인 0에서 멀리 떨어진) $dl/d\theta$ 가 자주 발생한다.

로그 우도 함수의 도함수

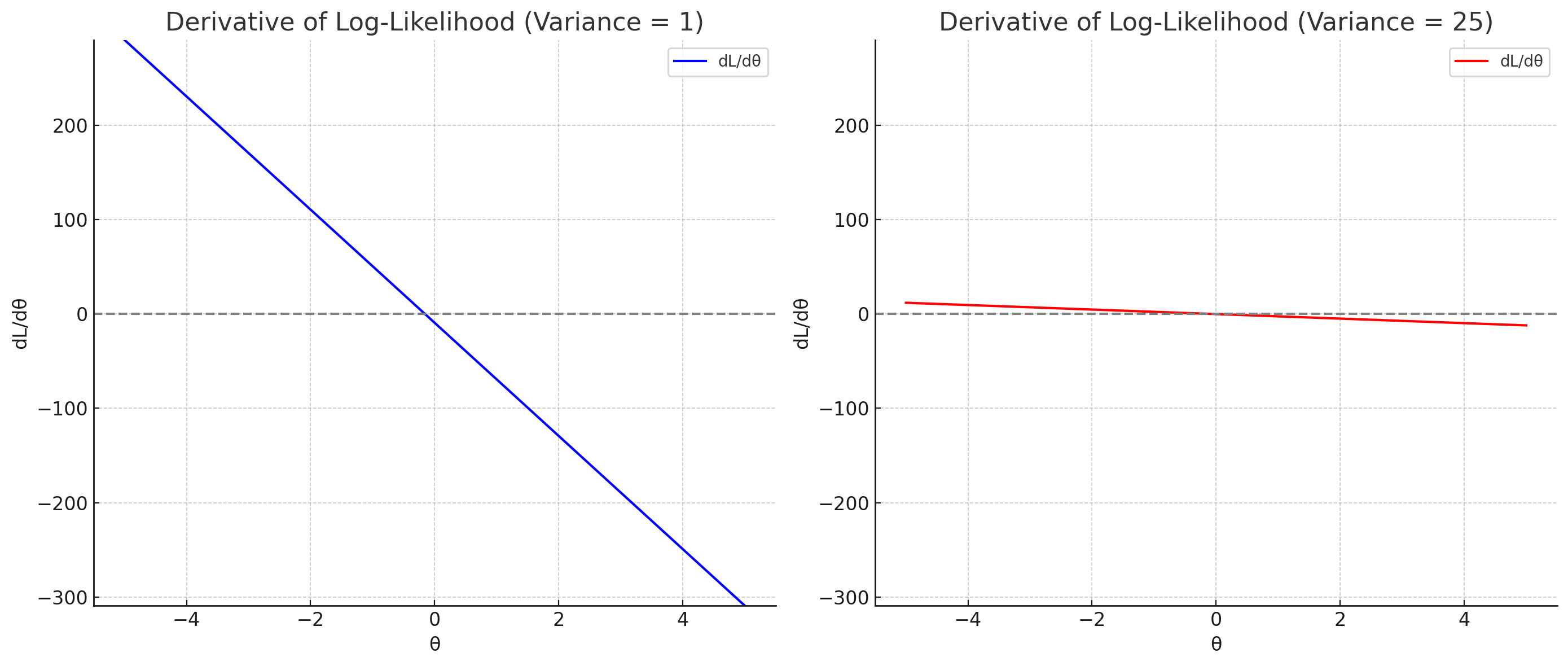
왼쪽 플롯은 위에서 $\frac{\partial}{\partial \theta} l(\theta)$ 의 분산이 컸던 경우를 의미한다. 분산이 크기 때문에 도함수들의 기울기 크기가 큰 것을 알 수 있다. 도함수의 기울기가 크다는 것은 $l_{\theta_1}(\theta)$ 의 곡률이 크다는 것이고, 극점이 매우 뾰족하게 나타날 것이다.

반대로 오른쪽 플롯은 분산이 작았다. 따라서 도함수의 기울기 크기가 0 근처에 뽑힐 것이고, 왼쪽과 비교했을 때 훨씬 완만한 것을 알 수 있다. 이 경우 반대로 곡률이 상대적으로 작고, 극점에서도 주변의 값과 차이가 거의 없이 완만하다고 볼 수 있다.

곡률에서 알 수 있는 것

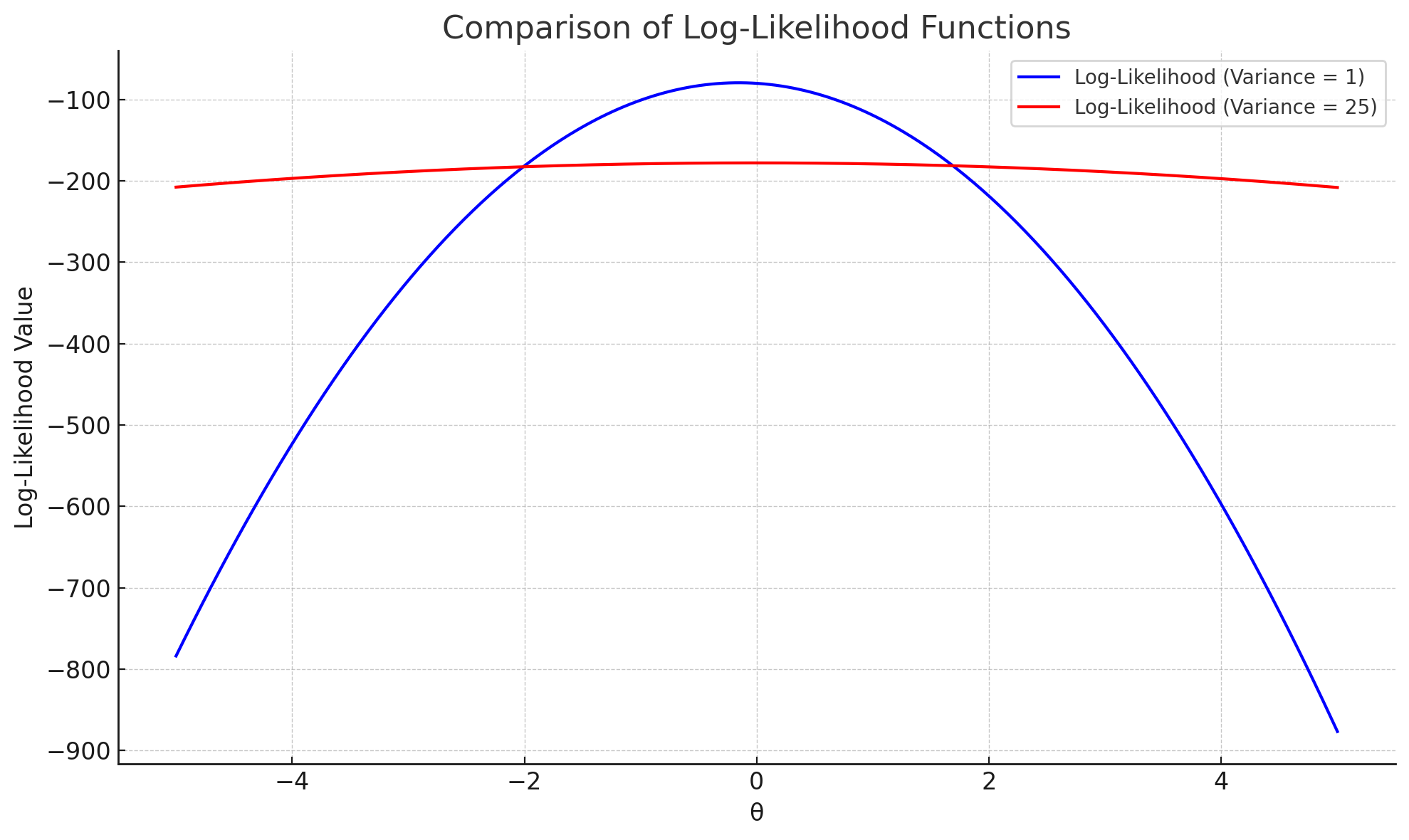
마지막으로 로그 우도 함수를 시각화해서 실제로 극점에서 완만함의 차이를 확인하자.

우리의 목표는 최대 우도 추정량; 즉, 로그 우도 함수를 최대화 하는 $\theta$ 를 찾는 것이다.
두 분포의 모평균이 0이라는 것을 아예 모르는 상황일 때, 곡률이 큰 $\sigma^2 = 1$ 의 경우 $\theta = 0$ 에서 함수가 매우 뾰족하다. 따라서 $\theta=0$ 에서 함수가 최대값을 가짐을 파악하기 쉽다.