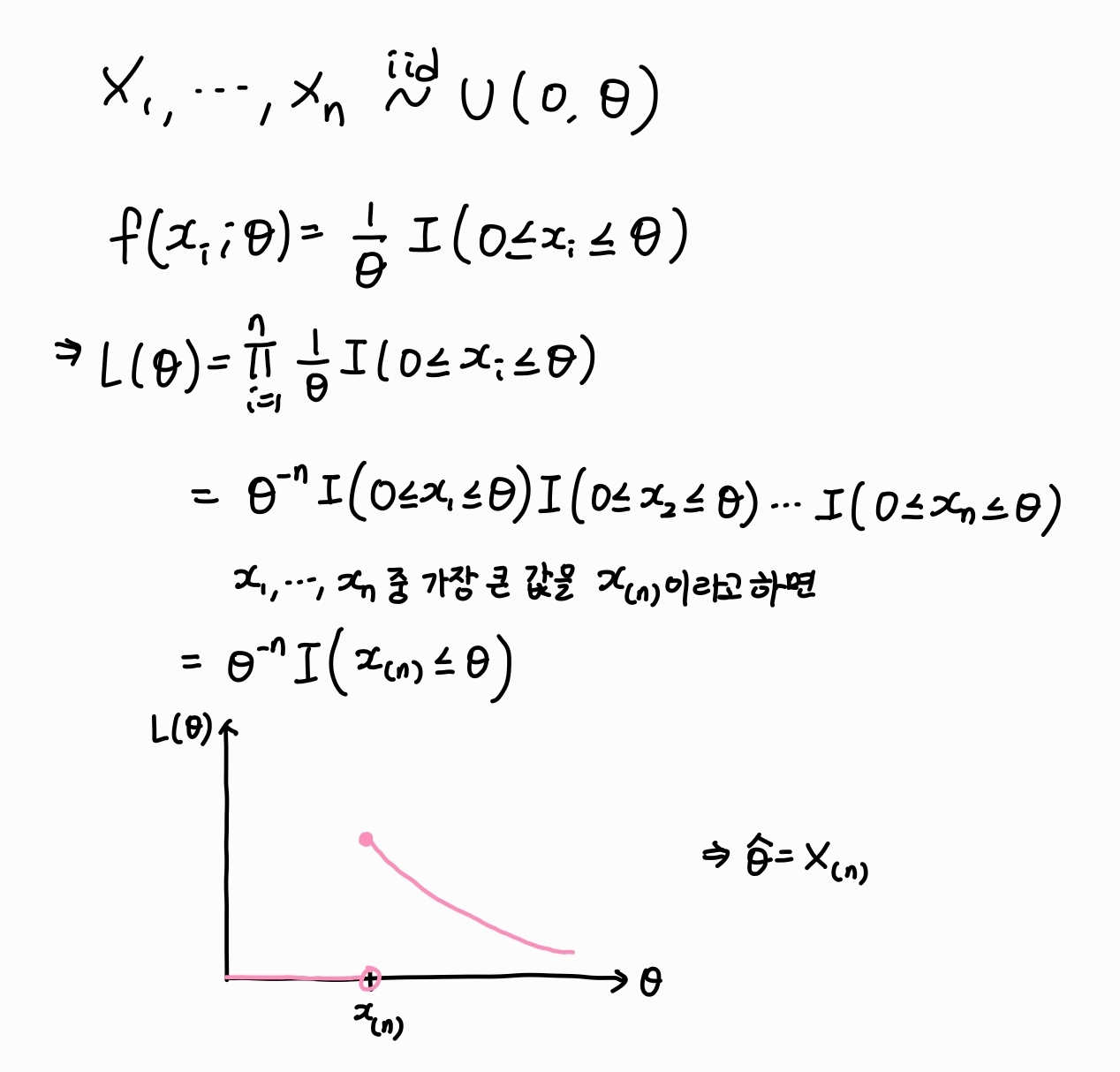우도 함수
이 동일한 pdf 에서 각각 독립적으로 추출된 랜덤 표본이라고 하자.
를 우도 함수(likelihood function)이라고 정의한다.
우도 함수는 랜덤 표본의 실현 이 주어졌다고 가정할 때, 임의의 에 대해 실제 모수가 인 경우 이 랜덤 표본으로 추출될 가능성을 계산한다. 직관적으로 이야기 하면 표본이 어떤 분포에서 뽑혔는지는 알겠는데(예상했는데), 모수가 어떤 값일 때 이런 표본이 나오는 것이 가장 자연스러울까(가능성이 높을까)를 수치화 한 함수다.
따라서 동일한 에 대해서도 표본의 실현 이 다르게 주어진다면 의 값은 변한다.
예를 들어 첫번째 표본의 실현 과 두번째 표본의 실현 이 주어졌다고 하자. 라면 의 값과 의 값은 다를 것이고, 따라서 와 는 달라지게 된다.
따라서 우리의 관심은 자연스럽게 우도 함수를 최대화 하는 로 가게 된다. 그런 가 존재한다면 수학적으로 뽑힌 표본을 가장 잘 설명할 수 있는 경우의 수가 되기 때문이다. 우도 함수의 최대값을 만족하는 를 찾는 과정을 최대 우도 추정법(Maximum Likelihood Estimation)이라고 한다.
로그 우도 함수
우도 함수는 확률 함수들의 곱으로 정의되기 때문에 미분 연산이 복잡해진다는 단점이 있다. 따라서 우도 함수에 로그를 씌워서 곱을 합으로 바꿔준다면 미분 연산을 비교적 쉽게 할 수 있다.
를 로그-우도 함수라고 정의한다.
로그 함수는 단조 증가 함수이므로 로그-우도 함수는 원래의 우도 함수가 극점을 가지는 곳에서 동일하게 극점을 가진다. 따라서 로그-우도 함수가 최댓값을 가지는 와 원래 우도 함수가 최댓값을 가지는 는 동일하다.
최대 우도 추정량
최대 우도 추정법에 의해 혹은 를 최대화 하는 를 찾아야 하기 때문에, 함수를 미분해서 미분계수가 0이 되는 극점 중에서, 이계도함수의 값이 음수인 점을 탐색한다. 만약 그러한 점 가 존재하는 경우 를 최대 우도 추정량이라고 한다.
가 스칼라가 아닌 벡터의 경우도 비슷하다. 함수를 각 에 대해 미분한 기울기 벡터를 구한 후, 기울기 벡터가 0이 되는 값을 찾는다. 이 때 함수의 이계도함수는 헤세 행렬의 꼴로 나타난다. 만약 헤세 행렬의 고유값이 위에서 구한 벡터 에서 모두 음수면 극대점이므로 최대 우도 추정량이 된다.
최대 우도 추정량 유도 예시
1. 지수 분포
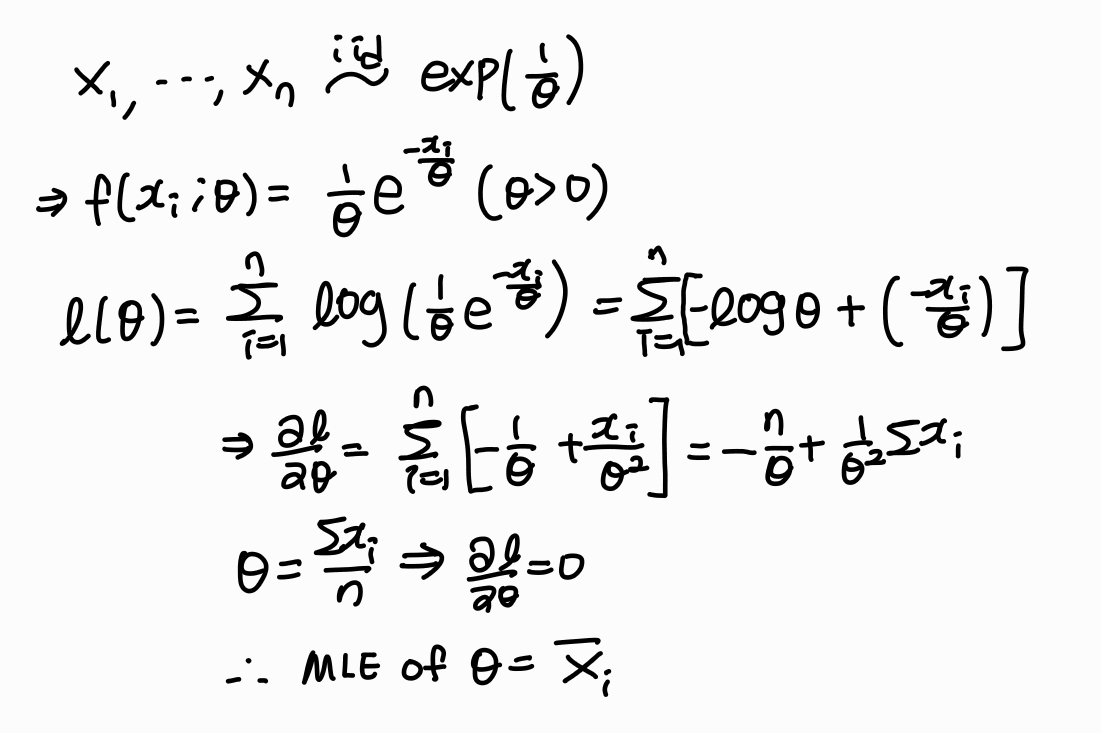
2. 라플라스 분포
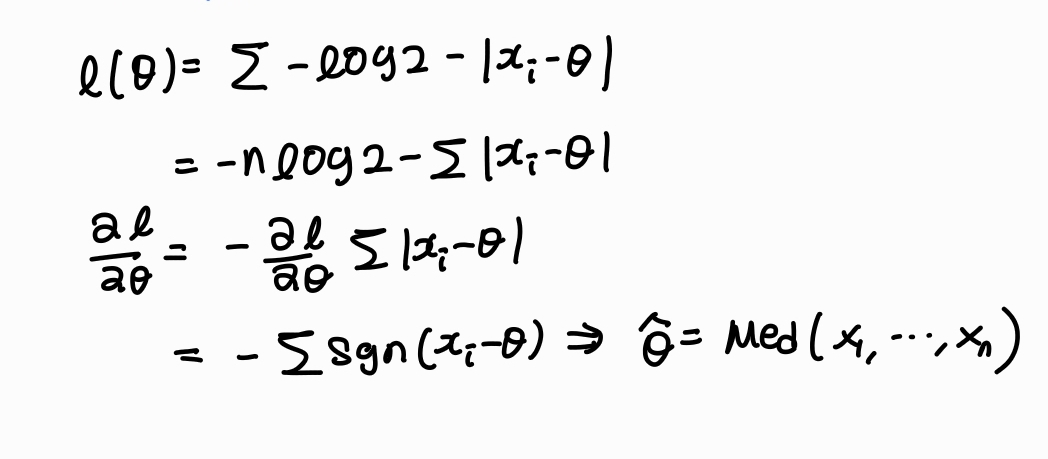
3. 로지스틱 분포
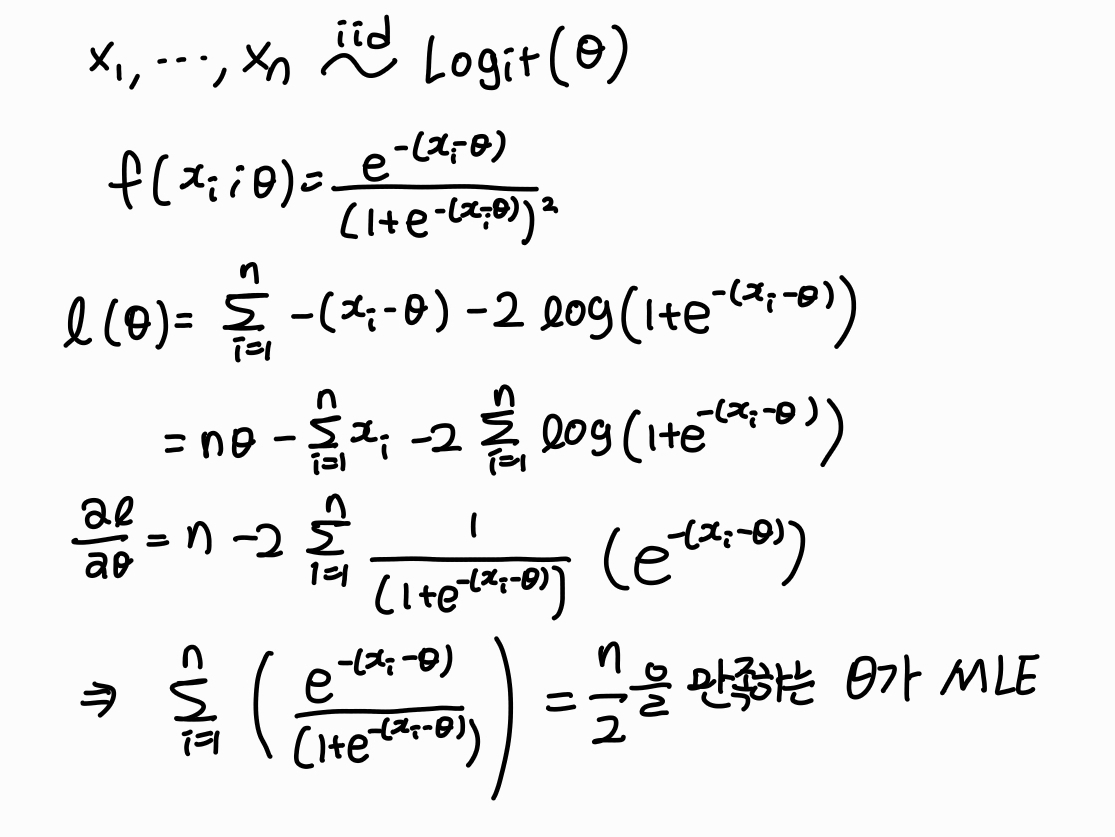
4. 균등 분포