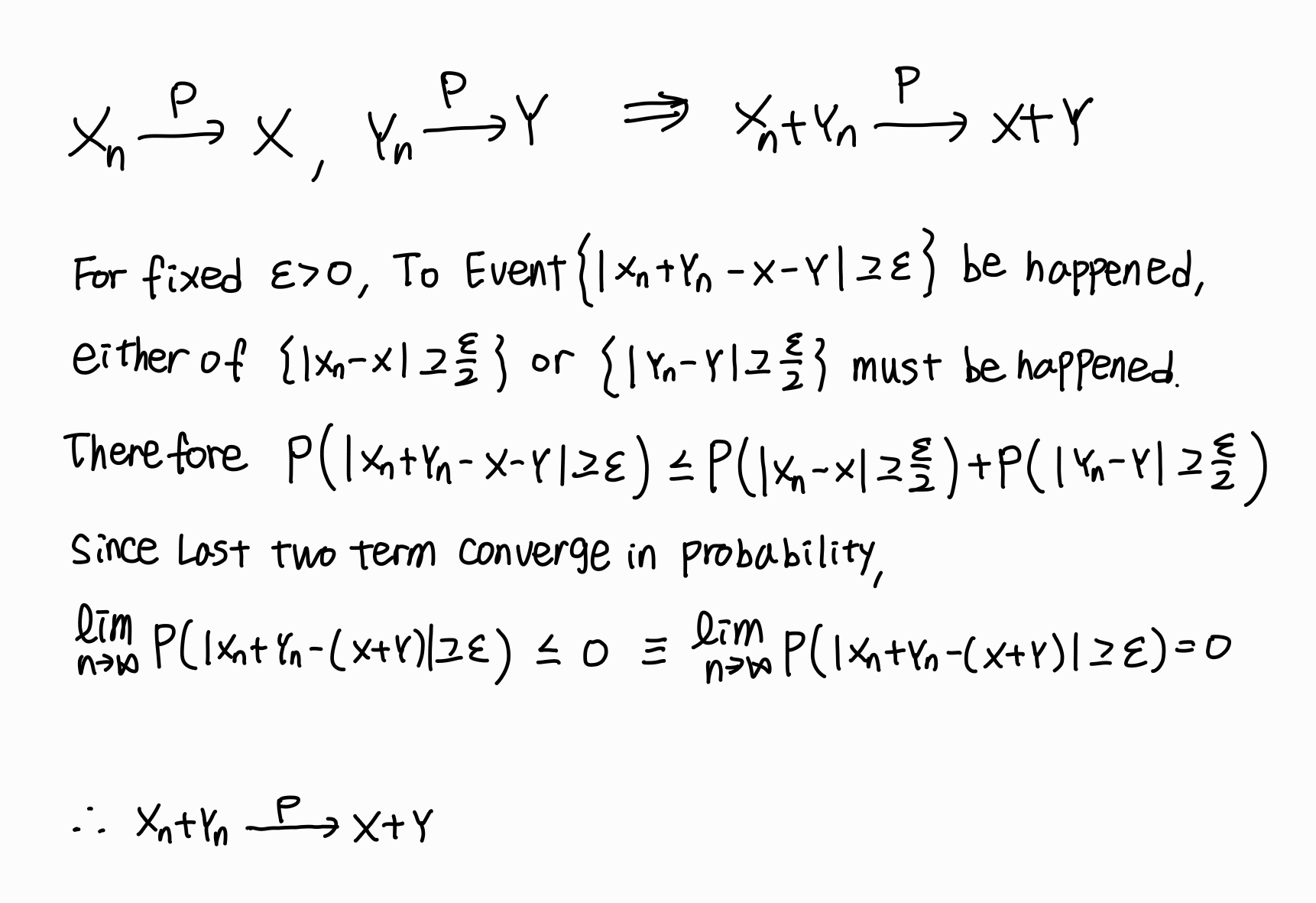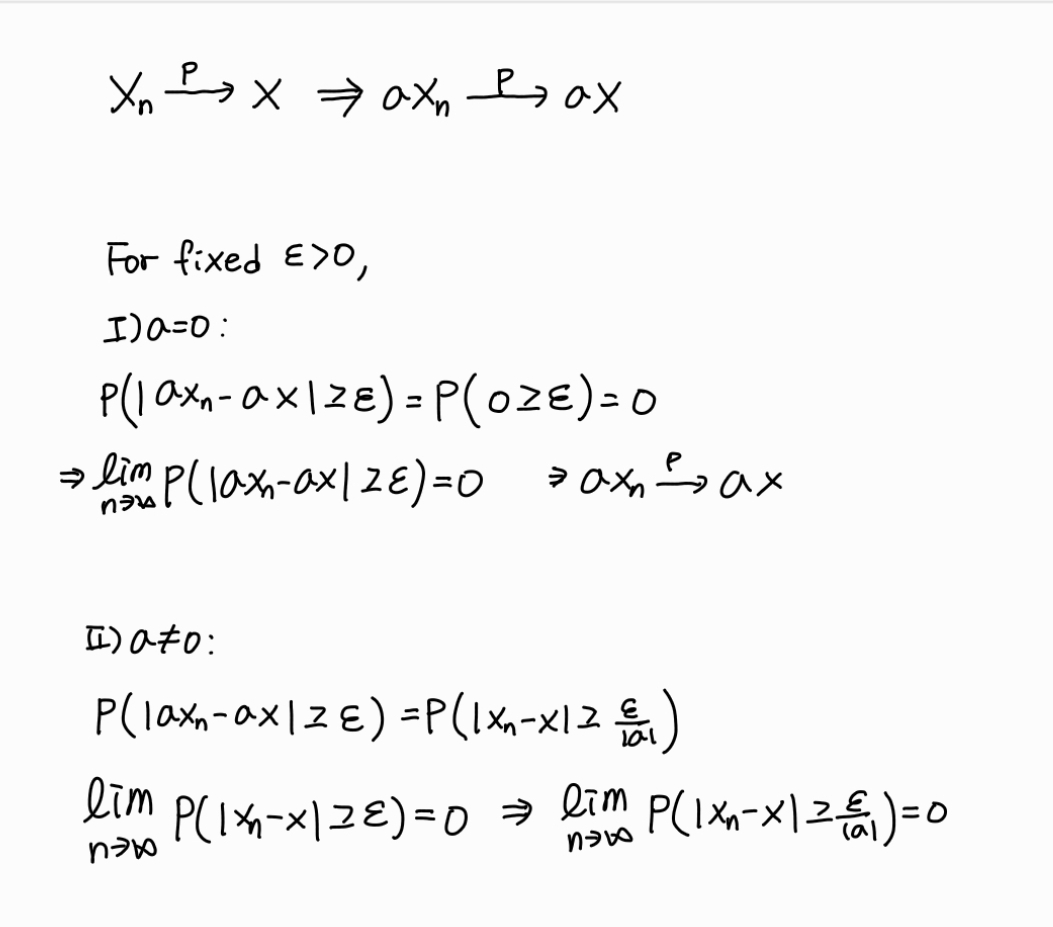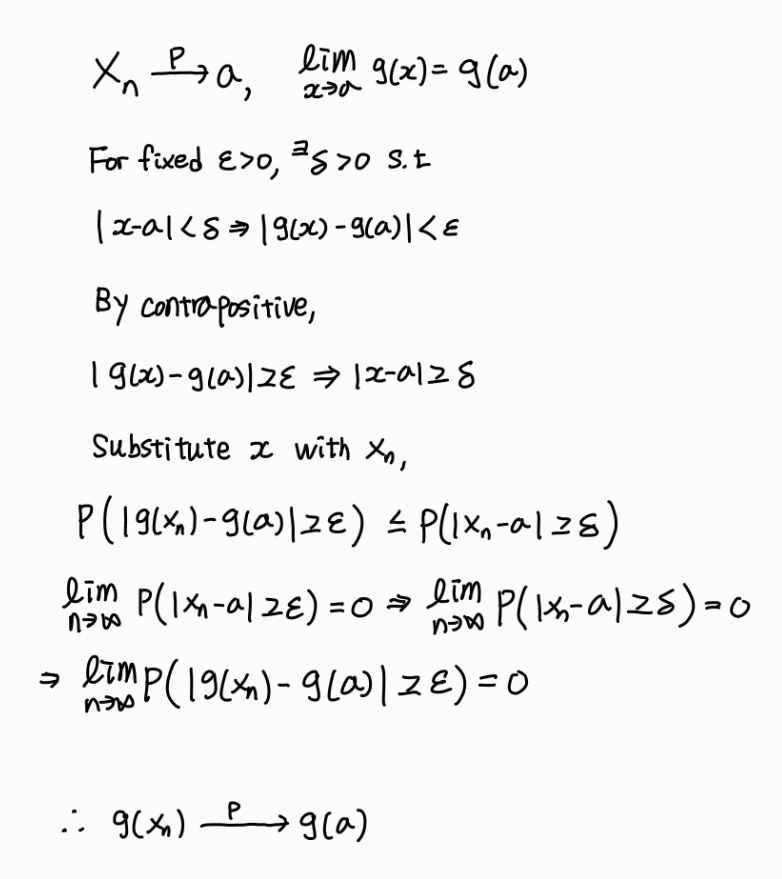확률 수렴의 성질, 추정량의 일치성

확률 수렴의 성질

확률 수렴하는 확률변수열은 유용하게 사용될 수 있는 몇가지 성질들을 가진다.

1. 확률 수렴하는 확률변수열의 합
   

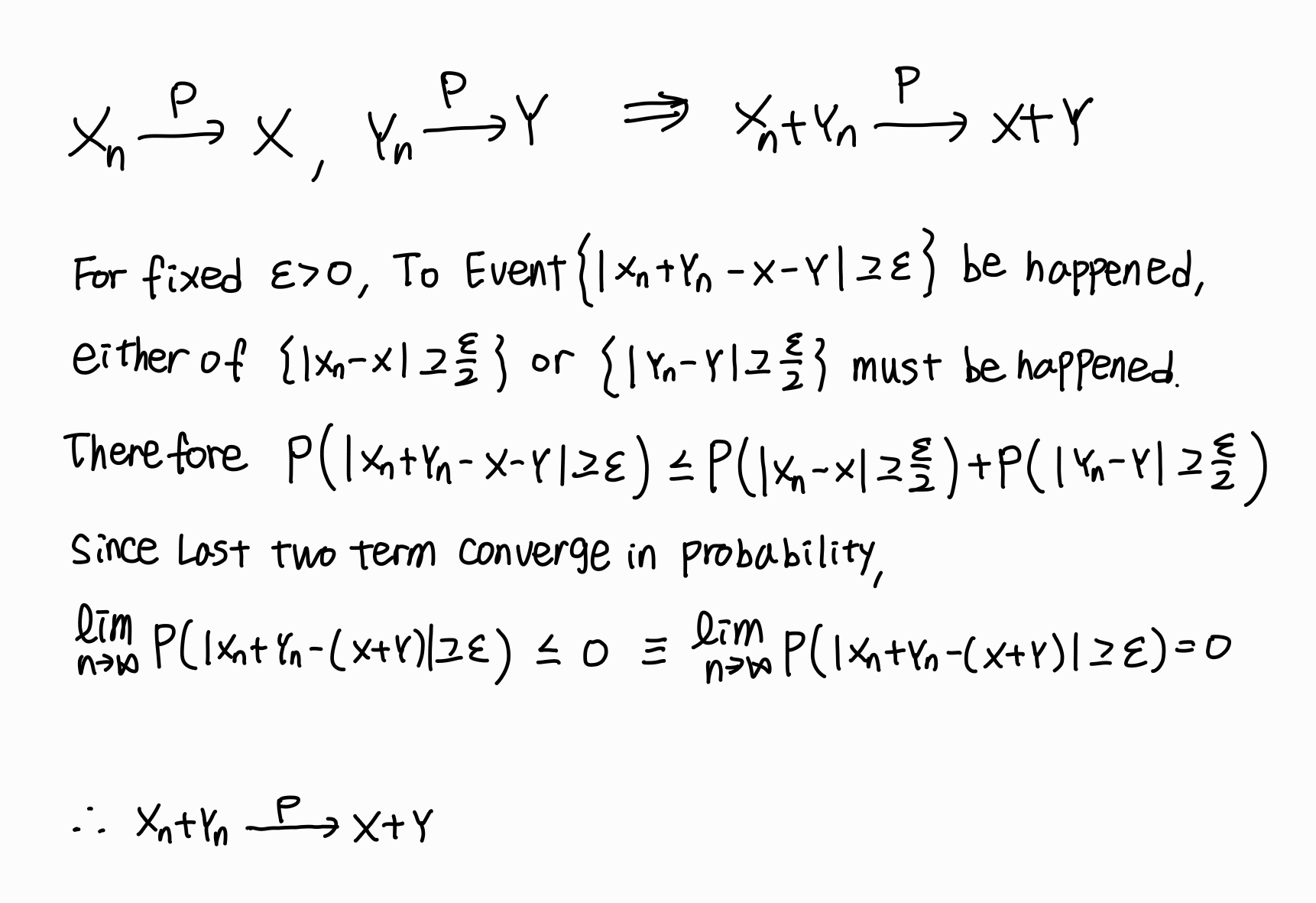
2. 상수배된 확률 수렴하는 확률변수열
   

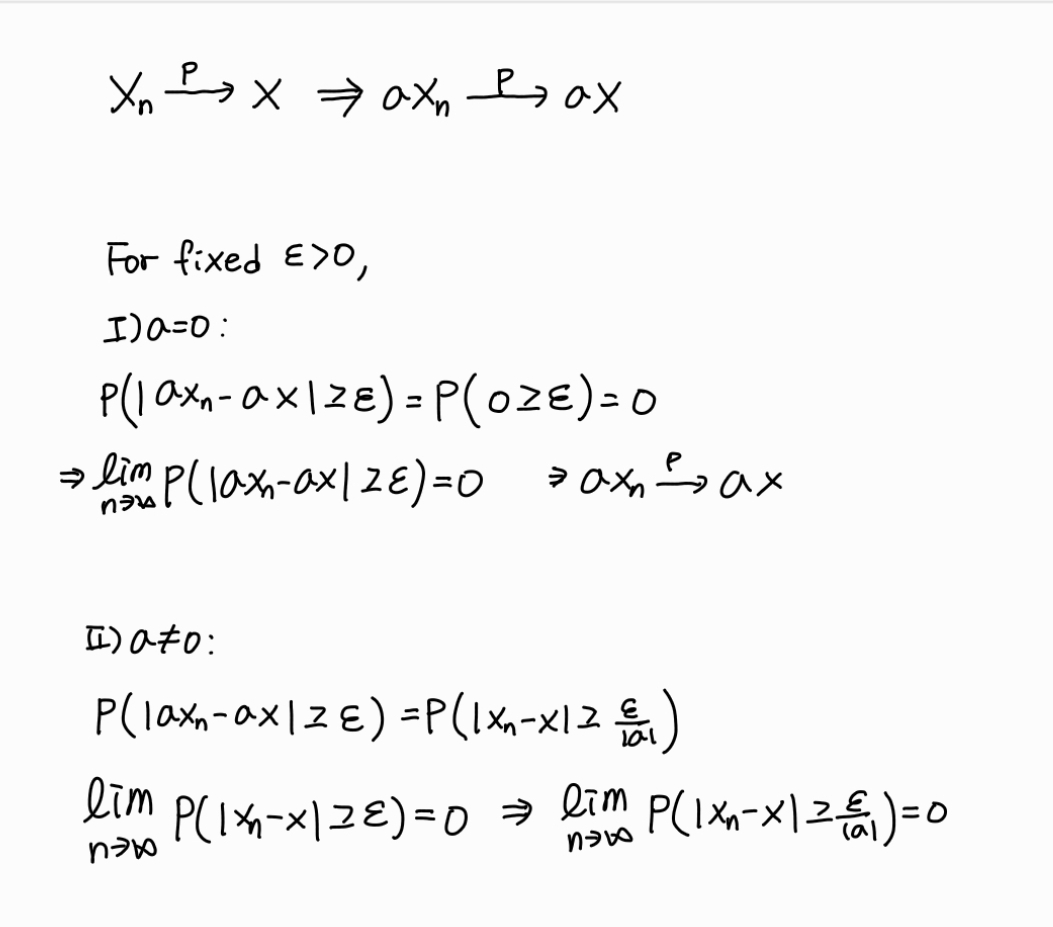
3. x=a에서 연속인 함수 g에 대한 확률 수렴
   

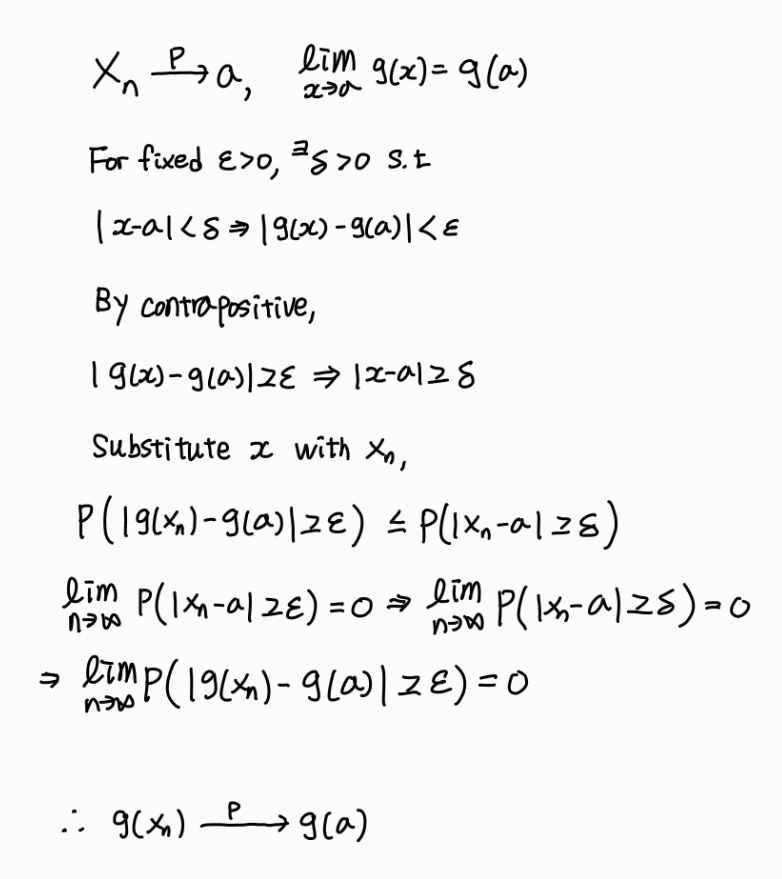
추정량의 일치성

모수 $\theta$에 대한 추정량 $T_n$이 있을 때, $T_n \rightarrow^P \theta$, 즉 $T_n$이 $\theta$로 확률 수렴하면 $T_n$을 일치추정량이라고 한다.

표본분산의 추정량 특성

$X_1, X_2, ..., X_n$이 $X$의 랜덤 표본일 때, 표본 분산은 다음과 같다.

1. 불편성

   $E(S_n^2) = E(\frac{\sum_{i=1}^n (X_i - \bar{X}_n)^2}{n-1}) = \frac{n}{n-1}[E(X_1^2) - E(\bar{X_n}^2)] \\ {} \\ = \frac{n}{n-1}[E(X_1^2)-\frac{\sigma^2}{n}-E(X_1)^2] = \frac{n}{n-1} \cdot \frac{n-1}{n}\cdot \sigma^2 = \sigma^2 \\ {} \\ \therefore E(S_n^2) = \sigma^2$

2. 일치성

   $S_n^2 = \frac{n}{n-1}(\bar{X_i^2}-\bar{X_n}^2) \\ {} \\ \text{By Weak Law of Large Number, }\bar{X_i^2} \rightarrow^PE(X_1^2) \\ {} \\ \bar{X_n} \rightarrow^P E(X_1), g(X) = X^2 \text{ is continuous in } \R \Rightarrow \bar{X_n}^2 \rightarrow^P E(X_1)^2 \\ {} \\ \frac{n}{n-1} \rightarrow^P 1 \\ {} \\ \therefore S_n^2 = \frac{n}{n-1}(\bar{X_i^2}-\bar{X_n}^2) \rightarrow^P \sigma^2$

따라서 표본분산은 불편추정량이며 일치추정량이다. 기본적으로 표본분산의 기댓값은 $\sigma^2$이며, 표본 크기가 커질수록 $S_n^2$의 값이 $\sigma^2$과 가까울 확률이 높아진다는 경향성이 있다.