확률 수렴의 정의, 약한 대수의 법칙

실수열의 수렴

확률 변수의 수렴이라는 개념을 잘 이해하기 위해, 배경지식이 되는 실수열의 수렴을 알아보자.
실수열 $a_n$이 상수 $a$로 수렴하면 $lim_{n \rightarrow \infin}= a$이다.
직관적으로 $n$이 커질수록 $a_n$의 값은 $a$ 근처에 존재한다는 것을 의미한다.

확률 변수의 수렴 : 불확실성

확률 변수에도 실수열의 수렴과 비슷하게 "확률 변수의 값이 어떤 상수에 수렴한다"와 같은 정리가 있으면 매우 유용할 것이다.

그러나 확률 변수는 값의 불확실성(확률)을 내포하고 있기 때문에, 매 실험마다 확률 변수의 값은 바뀔 것이고, 따라서 항상 확률 변수가 어떤 상수로 수렴한다는 성질을 만들기가 힘들다.

대신 비슷한 아이디어를 빌려와서, "확률들이 점점 어떤 값 근처로 점점 몰린다"고 생각하면 완벽하지는 않지만 유용한 정리로 사용할 수 있다.

확률 수렴

확률 변수의 열 $\{X_n\}$과 상수 $a$가 있다고 하자. 이 때 다음을 만족하면 $X_n$은 $a$로 확률 수렴하고, $X_n \rightarrow^p a$로 표기한다.

정의를 직관적으로 이해하자면 다음과 같다.
실수열의 수렴의 아이디어를 빌려오면, $n$이 작은 경우에는 $a$에서 비교적 멀리 떨어진 값도 $X_n$의 값이 될 확률이 높다.

그러나 $n$이 점점 커질수록, $X_n$에서 $a$와 거리가 먼 값이 튀어나올 확률이 작아진다. 그림으로 보면 다음과 같다.

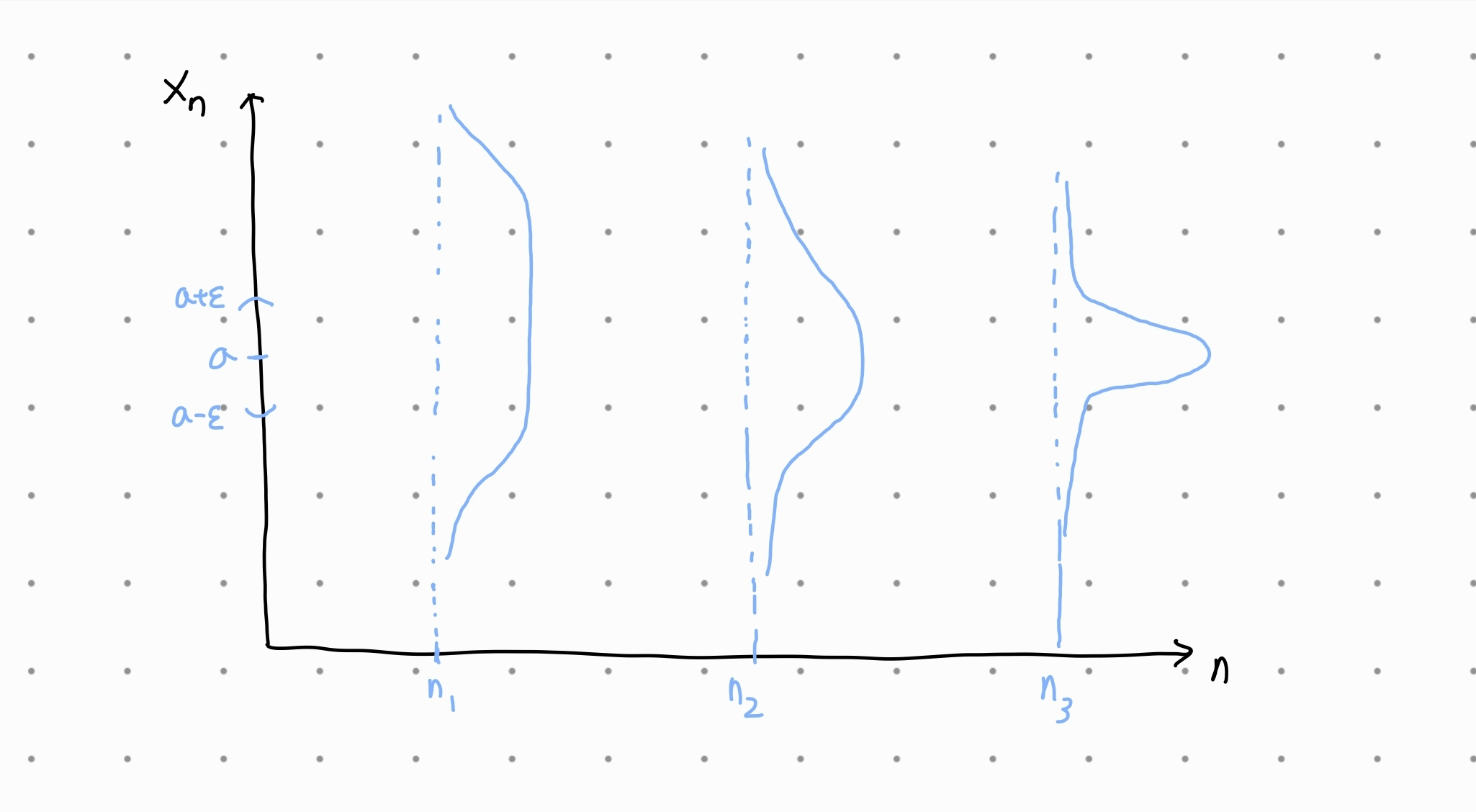
위 그림에서는 $n$이 점점 커짐에 따라 $a$에서 먼 값이 나올 확률이 줄어드는 것을 볼 수 있다.

모든 임의의 양수 $\epsilon$에 대해 이 현상이 성립하려면, n이 커질수록 위와 같은 확률이 $a$에 가깝게 점점 모이는 추세가 계속 되어야 한다.

따라서 확률변수열 $\{X_n\}$이 상수 $a$로 확률 수렴한다는 것은 $n$이 커짐에 따라 $X_n$의 값이 $a$ 근처가 될 확률이 높다는 의미다.

하지만 아무리 $a$에서 먼 값이 나올 확률이 낮다고 해도, 확률이 0이 아닌 이상 발생할 수도 있기 때문에 어떤 충분히 큰 n에 대해 $P(a - \epsilon < X_n < a + \epsilon) = 1$이라는 명제는 거짓이다.

확률 수렴은 $X_n$이 항상 $a$ 근처라는 "보장"은 못하지만, "경향성"은 설명할 수 있는 유용한 정리로 활용된다.

약한 대수의 법칙 (Weak Law of Large Number)

확률 수렴의 응용 예시로 약한 대수의 법칙을 들 수 있다. 약한 대수의 법칙은 표본 크기가 커질수록 표본 평균이 모평균과 비슷해지는 "경향성"이 있다는 것을 증명한다.