1. MDP - Markov Decision Process

MDP 가정

• environment가 fully observable 하다

• Machine의 state는 markov property 를 갖는다
  $P[S_{t+1}|S_t]=P[S_{t+1}|S_1,...,S_t]$
  즉, 이전 state에 상관없이 바로 직전 state에만 영향을 받는다.

• Markov Process는 set of finite state인 S와 state transition probability matrix P의 튜플을 의미한다.
  State transition matrix는 아래와 같은 식을 의미하며 $P_{ss'}$은 state s에서 s'으로 갈 확률을 의미한다.
  $P=\begin{bmatrix} P_{11} &...&P_{1n} \\ \vdots \\P_{n1} & ... & P_{nn} \end{bmatrix}$
  그리고 이 때 각 행의 합은 1이다.

Markov Reward Process

• 위의 Markov Process에 Reward 개념을 더한 process를 의미한다.
  $R_s=E[R_{t+1}|S_t=s]$ 이고 현재 시간에 대한 reward이지만 시간은 t+1임에 유의하자

• Return $G_t$는 아래와 같이 정의되고 $\gamma$는 discount factor로 미래에 얻는 수익은 감산하여 취급된다고 이해하면 된다 (금전적인 보상의 경우 이율을 의미할 수 있고 생명체가 얻는 보상의 경우 현재 이득을 더욱 값지게 느낀다는 형태로 이해)
  $G_t=R_{t+1}+\gamma R_{t+2}+...$

• state value function v(s)는 현재 state가 s일 경우 expected return 을 나타내는 함수이고 수식으로는 아래와 같이 표현된다
  $v(s)=E[G_t |S_t=s]$

• state value function 에서 Bellman equation을 도출할 수 있다.

Bellman equation for MRP (Markov Reward Process)

• 위의 value function 을 이용해 Bellman equation을 도출하는 과정은 아래와 같다.

$\begin{aligned} v(s)&=E[G_t |S_t=s]\\ &= E[R_{t+1}+\gamma R_{t+2}+...|S_t=s]\\ &=E[R_{t+1}+\gamma G_{t+1}|S_t=s]\\ &=E[R_{t+1}+\gamma E[G_{t+1}]|S_t=s] \\ &=E[R_{t+1}+\gamma v(S_{t+1})|S_t=s] \\ &=R_s + \gamma \sum_{s'\in S}P_{ss'}v(s') \end{aligned}$
다이어그램으로 나타내면 아래와 같다.

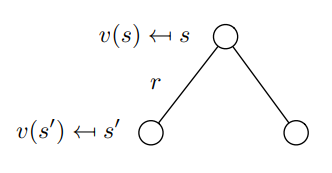
• value function은 역행렬로 연산가능 하지만 state 개수 n에 대해 $O(n^3)$ 의 time complexity를 갖기 때문에 향후 우리는 DP, Monte Carlo, Temporal-Difference 방법에 대해 배우게 된다.

Markov Decision Process

• Markov Reward Process에 finite action set A가 추가되며 state transition probability matrix와 reward function 에 action A에 대한 조건이 추가된다.
  $P_{ss'}^a=P[S_{t+1}=s'|S_t=s,A_t=a]\\ R_s^a=E[R_{t_+1}|S_t=s,A_t=a]$

• policy는 아래와 같이 정의된다.
  $\pi(a|s)=P[A_t=a|S_t=s]$
  이로부터 deterministic policy가 아닌 state s에서 어떤 action a를 취할 probability를 나타내는 stochastic한 방식을 택함을 알 수 있다

• MDP에서 MRP로의 변환방법은 아래와 같다. 둘의 차이는 state transition probability matrix와 reward function에 있고 MDP에서 모든 action에 대해 합을 구한다면 action에 대해 고려하지 않은 MRP를 구할 수 있을 것이고 수식은 아래와 같다
  $P_{ss'}^\pi=\sum_{a\in A}\pi{(a|s)}P_{ss'}^a \\ R_s^\pi=\sum_{a\in A}\pi(a|s)R_s^a$

• value function은 이제 policy dependent하게 계산되며 식은 아래와 같다.
  $v_\pi(s)=E_{\pi}[G_t|S_t=s]$
  새로운 개념인 action-value function이 도입되며 식은 아래와 같다.
  $q_\pi(s,a)=E_\pi[G_t|S_t=s,A_t=a]$
  현재 state가 s이고 취하는 action이 a일 때 얻을 수 있는 return의 기대값을 의미한다.

Bellman equation for MDP (Markov Decision Process)

• 직관적인 표현식은 각각 다음과 같다.
  $v_\pi(s)=\sum_{a\in A}\pi(a|s)q_\pi(s,a) \quad ...(1)\\ q_\pi(s,a)=R_s^a+\gamma \sum_{s'\in S}P_{ss'}^av_\pi(s') \quad ...(2)$
  
  
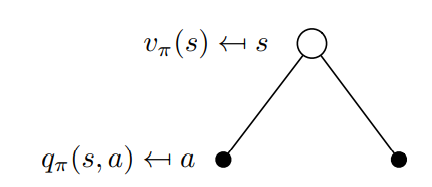
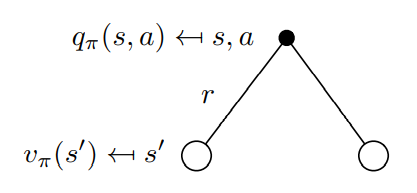
  수식 (1)은 모든 action에 대한 확률과 action시 reward를 곱한 값으로 다음 action에 대한 기대값으로 이해할 수 있다.
  수식 (2)는 현재 택한 action에 대한 reward $R_s^a$와 action 으로 인해 전환된 다음 state s'에서 얻을 return 의 기대값을 더한 것으로 이해할 수 있다.

• 이로부터 value function 은 value function으로만, state value function은 state value function 으로만 표현하면 아래와 같다.
  $v_\pi(s)=\sum_{a\in A}\pi(a|s)(R_s^a+\gamma \sum_{s'\in S}P_{ss'}^av_\pi(s')) \\ q_\pi(s,a)=R_s^a+\gamma\sum_{s'\in S}P_{ss'}^a\sum_{a'\in A}\pi(a'|s')q_\pi(s',a')$

optimal value function

• optimal state-value function 과 optimal action-value function은 각각 모든 policy에 대해 최대 값을 갖는 함수를 나타낸다.
  $v_*(s)=max\,v_\pi(s) \\ q_*(s,a)=max\,q_\pi(s,a)$

optimal policy

• 어떤 Markov Decision Process에 대해서도 $\pi_* \geq \pi \quad \forall \pi$를 만족하는 optimal policy $\pi_*$가 존재한다.
  그리고 이 policy는 optimal value function을 도출한다.

• optimal policy를 찾는 법은 optimal action value function에서 모든 action 들 중 가장 값을 최대로 만드는 action을 찾고 stochastic action 표현에서 그 action 에 대해서만 확률 1을 갖도록 만들면 되기 때문에 아래와 같이 표현가능하다.
  $\pi_*(a|s)=\begin{cases} 1 & \text if \quad a=argmax_{a \in A} \; q_*(s,a) \\ 0 & \text otherwise \end{cases}$

Bellman optimality equation

• optimal value function은 다음과 같이 표현될 수 있다.
  $v_*(s)=max\;q_*(s,a)$
  $q_*(s,a)=R_s^a+\gamma \sum_{s'\in S}P_{ss'}^av_*(s') \\$
  위 식을 각각 다시 자신만을 사용해서 나타내면 아래와 같다
  $v_*(s)=max\; (R_s^a+\gamma \sum_{s'\in S}P_{ss'}^av_*(s'))$
  $q_*(s,a)=R_s^a+\gamma \sum_{s'\in S}P_{ss'}^amax\;q_*(s',a' )$

• Bellman Optimality Equation은 max 함수 때문에 non-linear 하므로 iterative 한 방식으로 접근해야 한다.