Attention is all you need - Transformer

1. Attention 아이디어

decoder 에서 출력 단어를 예측하는 시점에서 인코더 전체 문장을 참고하는데 전체를 같은 비율로 참고하는 것이 아닌 해당 시점에서 예측해야 할 단어와 연관있는 단어에 비중을 두어 참고

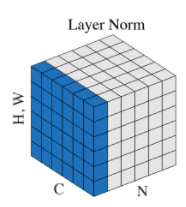
• 디코더에서 attention 계산이 일어나는 과정
  Query : t 시점에서 디코더 셀의 은닉상태
  Key : 모든 시점에서 인코더 셀의 은닉상태
  Value : 모든 시점에서 인코더 셀의 은닉상태
  현재 Query 가 봐야할 값은 Key와 dot product을 통해 그 연관성을 계산하고 Value에 weight로 곱해져 최종적으로 참고해야 할 결과를 얻는다

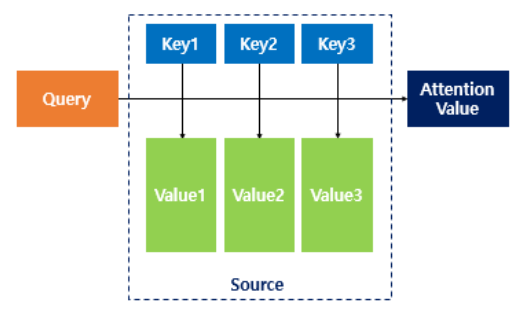
• Query, Key, Value 계산에 대한 이해
  (차원의 측면에서)
  $d_{model}$ 이 embedding vector의 차원을 의미할 때 한 단어 토큰에 대해 key, query, value가 갖는 dimension인 $d_k$ 혹은 $d_v$ 는 multihead attention의 head 개수가 n개 일 때
  $d_k$ or $d_v$ = $\frac{d_{model}}{n}$ 으로 결정된다.
  그러므로 우리는 각각의 단어 토큰에 대해 각각의 query, key, value를 구하기 위해 $R^{d_{model}\times d_{v}}$ 차원의 weight를 갖게 되며 아래의 그림과 같이 도식화하여 표현할 수 있다.
  

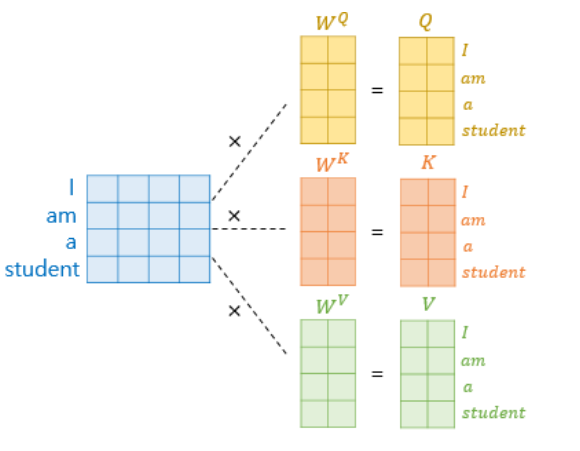
• Attention 값이 계산과정
  
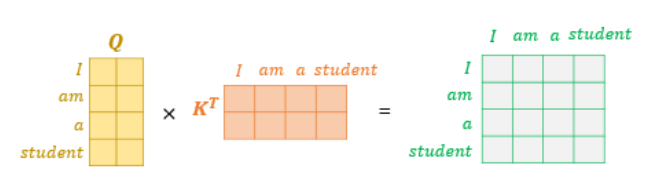
  위의 그림과 같이 어떤 쿼리에 대해 각 key 값들이 갖는 연관성을 Matrix multiplication 형태로 한번에 계산할 수 있고 하나의 query에 대해 softmax를 취해 [0,1]로 다른 토큰과의 영향성을 정규화 할 수 있다.

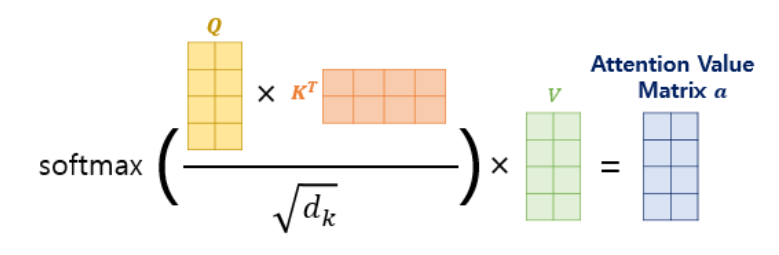
위에서 계산한 attention에 value를 곱해 얻은 attention value matrix는 아래와 같은 수식으로 표현된다 .
$Attention(Q,K,V) = softmax(\frac{QK^T}{\sqrt{d_k}}V)$

• Scaled dot Product Attention을 사용하는 이유
  dot Product를 통해 얻은 attention을 바로 사용하지 않고 scalar 값으로 나눠주는 이유는 softmax의 backpropagation 과정을 살펴보면 알 수 있다.
  먼저 softmax의 성질을 알아야 하는데 softmax에서 scale 값이 클수록 큰 값은 1에 근접하고 작은 값은 0으로 근접한다는 것을 알 수 있다.
  $R^n$ 차원을 갖는 벡터 z가 softmax를 통과한 이후 얻는 벡터를 s 라 하자
  이는 $R^n \rightarrow R^n$ 으로 가는 함수이기 때문에 Jacobian matrix는 아래와 같이 표현될 수 있다.
  $J_{soft} = \begin{pmatrix}\frac{\partial s_1}{\partial j_1} &\frac{\partial s_1}{\partial j_2}&...&\frac{\partial s_1}{\partial j_n}\\\frac{\partial s_2}{\partial j_1}&\frac{\partial s_2}{\partial j_2} &...&\frac{\partial s_2}{\partial j_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial s_n}{\partial j_1} & \frac{\partial s_n}{\partial j_2} & ... & \frac{\partial s_n}{\partial j_n} \end{pmatrix}$
  이 때 i 번째 softmax 원소의 j 번째 변수에 대한 편미분, 즉 Jacobian Matrix의 (i,j)번째 원소는 아래와 같이 표현가능하다.
  $\frac{\partial s_i}{\partial z_j}=s_i*(1\{i=j\}-s_j)$
  n=4 인 경우 아래와 같으며 대칭 행렬이라는 것을 알 수 있다.
  
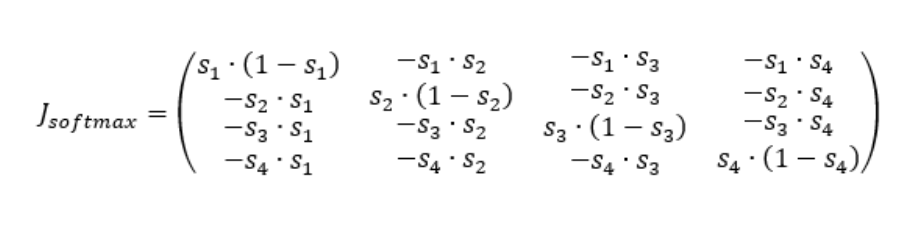
  이제 backpropagation에 대해 계산해보자
  앞서 s가 z를 softmax 한 결과임을 가정했으므로 backpropagation에서는 z에 대한 미분이 나중에 얻어질 것이며 수식으로는 아래와 같이 계산된다.
  $\frac{\partial L}{\partial z_j}=\sum_{i=1}^n \frac{\partial L}{\partial s_i}*\frac{\partial s_i}{\partial z_j}=\begin{pmatrix} \frac{\partial s_1}{\partial z_j} &\frac{\partial s_2}{\partial z_j}&...&\frac{\partial s_n}{\partial z_j} \end{pmatrix} *\begin{pmatrix} \frac{\partial L}{\partial s1} \\ \frac{\partial L}{\partial s_2} \\ \vdots \\ \frac{\partial L}{\partial s_n} \end{pmatrix}$
  앞선 항은 Jacobian Matrix의 j번째 column에 대응한다는 것을 알 수 있으므로 전체 s , v 벡터에 대해 일반화한다면
  $\frac{\partial L}{\partial z}=J_{soft}^T *\frac{\partial L}{\partial s}=J_{soft}\ *\frac{\partial L}{\partial s} (\because$ J is symetric $)$
  위의 결과에서 softmax 결과가 0이나 1에 가까워 지면 전체 jacobian이 0으로 수렴한다는 사실을 알 수 있고 이는 gradient 소멸과 연결된다는 것을 수식을 통해 파악할 수 있다.
  [참고]
  https://towardsdatascience.com/transformer-networks-a-mathematical-explanation-why-scaling-the-dot-products-leads-to-more-stable-414f87391500

2. Transformer안에 있는 attention의 종류

2.1 Self Attention

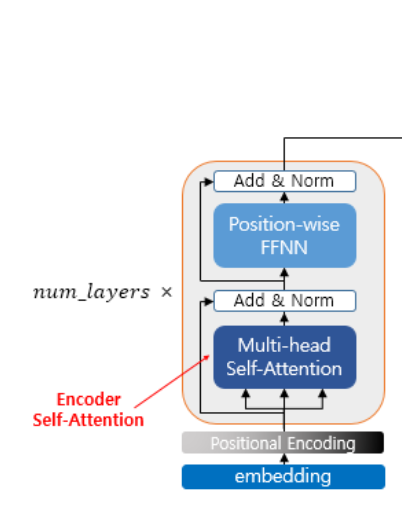
Transformer의 encoder 부분에서 같은 input으로부터 유래된 Q,K,V에 대해 attention 값 계산을 의미하며 아래와 같은 효과를 갖는다.

문맥 상에서 여러 의미를 가질 수 있는 it에 대해서도 문장 구조 상 어떤 의미를 가질 확률이 큰지 inference 할 수 있다.

2.2 Encoder - Decoder Attention

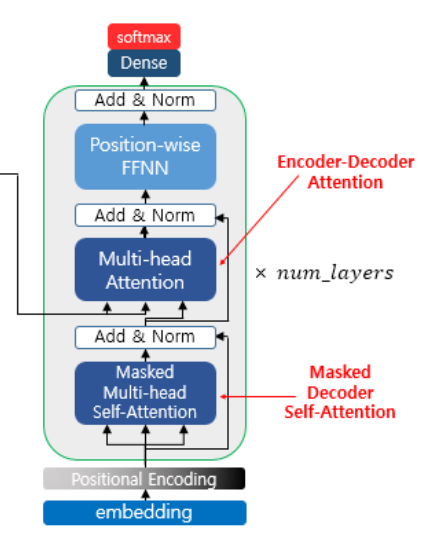
key 와 value는 encoder에서 발생한 것을 가져오는 반면 query는 decoder에서 발생한 것을 가져온다

2.3 Masked Decoder self Attention

Decoder는 원칙적으로 현재 시점 t 이후의 input 정보를 볼 수 없는 상태에서 훈련하는 것이 맞기 때문에 t+1 이후의 input 토큰들에 대해서는 masking 처리한 후 attention 값을 계산한다.
<pad> 토큰이나 decoder self attention을 mask 하기 위해 아주 작은 실수값을 곱해 0과 비슷하게 처리한다

2.4 Multihead attention

latent space에 있는 토큰 벡터들을 head 개수만큼 나눠 병렬적으로
$\frac{d_{model}}{n_{heads}}$ 크기의 벡터들에 대해 attention 연산을 진행한다.
이후 각각의 결과 vector들은 다시 concatenate 된 이후 $W_o$ 의 dense layer를 지나 최종적인 Attention 값으로 변환된다

Positional Encoding

RNN과 다르게 각 input 벡터에는 sequence 정보가 포함되어있지 않고 이를 보완하기 위해 주기함수를 각 input 벡터에 더해 성질을 부여할 수 있도록 하였다.
논문에서 사용한 주기 함수
$PE_{(pos,2i)}=sin(pos/10000^{2i/d_{model}})$
$PE_{(pos,2i+1)}=cos(pos/10000^{2i/d_{model}})$

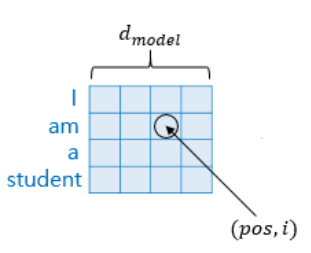
변수 pos는 문자열 내부에서 단어가 위치하는 index를 의미하며 $d_{model}$은 embedding vector의 차원, 트랜스포머의 출력 차원을 의미한다.
변수 i는 임베딩 벡터 안에서의 위치 index를 의미하며 도식화하여 쉽게 표현하면 아래와 같다.

FFN (Feed Forward Network)

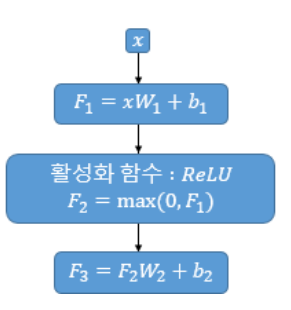
Attention 연산을 거친 벡터는 FFN block을 지나게 되는데 이는 FC layer-ReLU-FC layer의 구조로 이뤄져 있다.
입력 받는 x의 크기는 $R^{seq\times d_{model}}$ 이며 출력 dimension은 $R^{seq\times d_{ff}}$ 이다. 마지막 FC-layer를 통과하는 과정에서 $R^{seq\times d_{model}}$로 다시 변환된다.
논문에 사용된 $d_{ff} = 2048$ 이다.

Add and Norm

각각은 residual connection과 layer normalization을 의미하며 residual connection은 ResNet에서 봤던 skip connection과 동일한 개념으로 생각하면 되고 layer normalization은 batch가 아닌 layer 방향에 대한 normalization으로 아래의 그림과 같이 이래할 수 있다.