Dynamic programming 용어정리
- Prediction 이란 model 에 대한 정보 (MDP나 MRP)와 policy π가 주어졌을 때 value function을 구하는 과정을 의미한다.
- Control이란 MDP가 주어졌을 때 optimal value function과 optimal policy 계산을 의미한다.
- Policy evaluation 이란 주어진 policy π에 대해 vπ로 수렴하는 value function을 구하는 과정을 의미하고 iterative policy evaluation은 이런 과정을 반복적인 bellman expectation 적용을 통해 계산한다
Iterative Policy evalutaion
- policy 가 주어졌을 때, 앞서 1장에서 소개한 v로만 표현된 state value function에 대한 bellman equation 식으로부터 iterative 한 과정을 반복하며 아래의 수식에서 첨자 k는 iteration 횟수를 의미한다.
vπ(s)=∑a∈Aπ(a∣s)(Rsa+γ∑s′∈SPss′avπ(s′))vk+1(s)=∑a∈Aπ(a∣s)(Rsa+γ∑s′∈SPss′avk(s′))
위의 식은 원래 bellman equation을 나타낸 것이며 아래 식은 이를 iterative 버전으로 바꿨을 때 결과를 나타낸다.
Policy improvement
- action-value function을 최대로 만드는 action을 취할 경우 value function을 improve 한다는 사실을 증명할 수 있다.
먼저 policy는 deterministic 하다고 가정(a=π(s))하고 greedy 하게 행동하는 과정을 수식으로 아래와 같이 나타낸다.
π′(s)=argmaxa∈Aqπ(s,a)
이렇게 선택한 policy에 대해 action value function은 현재 state value function보다 크다는 것을 보일 수 있다.
qπ(s,π′(s))=maxa∈Aqπ(s,a)≥qπ(s,π(s))=vπ(s)
이제 qπ(s,π′(s))≤vπ′(s)임을 보이면 vπ(s)≤vπ′(s) 임을 보일 수 있다.
qπ(s,π′(s))=Eπ′[Rt+1+γvπ(St+1)∣St=s]≤Eπ′[Rt+1+γqπ(St+1,π′(St+1)∣St=s]≤Eπ′[Rt+1+γRt+2+γ2qπ(St+2,π′(St+2))∣St=s]≤Eπ′[Rt+1+γRt+2+...∣St=s]=vπ′(s)
- policy improvement가 중단되었을 때의 value function이 optimal policy 임은 아래의 식을 통해 알 수 있다.
qπ(s,π′(s))=maxa∈Aqπ(s,a)=qπ(s,π(s))=vπ(s)
한편 1장의 Bellman optimal equation 에 의하면 v∗(s)=maxq∗(s,a) 인데 현재 policy인 π가 이를 만족하고 있으므로
vπ(s)=v∗(s)∀s∈S 이다.
Policy iteration
- policyiteration=policyevaluation+policyimprovement
- 위의 과정은 policy evaluation 과정에 관해 설명했다면 이 절은 policy evalution 과 improvement를 합친 policy iteration에 관한 설명이고 아래의 수식과 같이 정리할 수 있다.
vπ(s)=E[Rt+1+γRt+2+...+∣St=s]π′=greedy(vπ)
policy를 평가하고 (V를 통해) 여기서 얻은 V 중 가장 greedy 하게 만드는 policy를 고르는 행위의 iteration을 통해 optimal 한 값에 수렴해 가며 아래의 그림과 같이 표현된다.
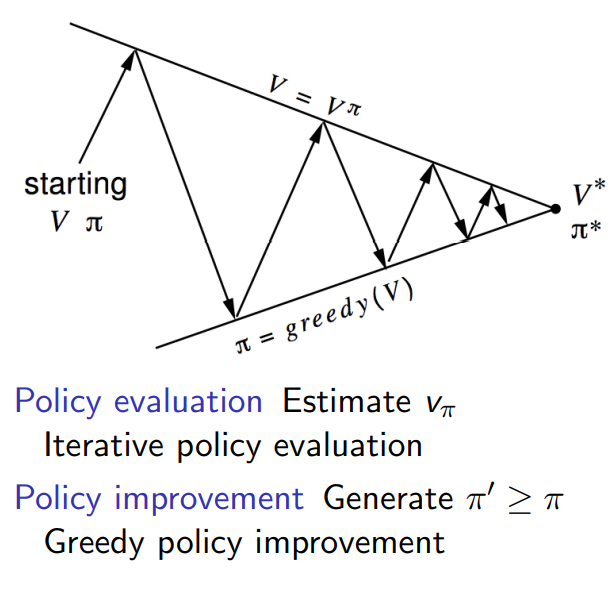
Policy iteration modified - Value iteration
- 위의 도표에서 V를 향하는 화살표는 policy evaluation을 의미하는데 여러번의 iteration을 통해 그 값에 도달한다. 하지만 매번 iteration을 과도하게 반복해 optimal에 도달하는게 좋은 방법인가?
Policy evaluation을 한번만 거치고 바로 policy를 update하는 value iteration 방식이 소개되었다.
- 위에서 설명한 것과 같이 value iteration은 한번의 policy evalution 이후 policy update를 진행하며 policy iteration 방식에서 bellman equation을 쓴 것과 다르게 여기서는 bellman optimality equation을 사용하며 수식은 아래와 같다.
vk+1(s)=maxa∈A(Rsa+γ∑s′∈SPss′avk(s′))
현재까지 Sum up
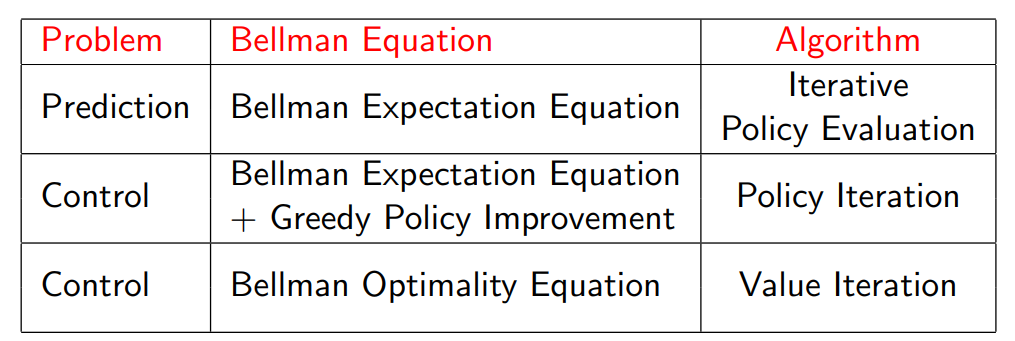
- prediction 문제와 control 문제는 전자는 policy가 주어진 경우 value function을 구하는 문제를 의미하며 후자는 MDP에 대해 optimal policy와 value function을 구하는 문제를 의미한다.
- policy iteration은 policy evaluation과 policy improvement로 구성되며 value iteration은 policy iteration에서 policy evaluation 부분이 한 번만 반복되는 경우를 의미한다.
- value iteration과 policy iteration은 반복 횟수에서만 차이를 갖는 것은 아니며 value iteration은 value function을 구할 때 Bellman optimality equation을 사용하고 policy iteration Bellman equation과 policy improvement 시 greedy 한 선택을 한다는 차이도 존재한다.
Asynchronous DP
- in place dynamic programming
vnew와vold에 대한 정보를 모두 담지 않고 바로 in place하게 iterate 하는 방식을 의미한다.
- prioritised Sweeping
각 state에 대해 Bellman error를 계산한 뒤 가장 큰 state에 대해 back up 한다. 각 backup 에 대해 영향받는 state들에 대해서만 Bellman error를 update한다. 이를 위해서는 priority queue를 사용해 가장 큰 bellman error를 갖는 state를 저장하고 각 state는 predecessor 정보를 갖고 있어야 한다.
- Real-time Dynamic Programming
Agent에 관련있는 state만 계산하는데 이러한 state의 목록을 고르는데에는 agent experience를 참고하도록 한다.
Full width backup 이란
- DP 는 각 backup에 대해 모든 successor state와 action에 대해 고려해야 하므로 Bellman's curse of dimensionality를 겪는다
state 개수와 시간 복잡도의 관계에 의해 large problem에는 적합하지 않ㄴ다.
- 이를 위한 대안으로 sample backup 개념이 도입되었으며 시간 복잡도에 대한 개선과 MDP를 몰라도 된다는 장점이 존재한다.
Iterative method의 convergence에 대한 증명


