이번 강의 목표
- Model-free Control
Control : MDP를 모르는 상황에서 value function optimize 하는 것
On-policy and Off-policy Learning
- On-policy: experience sample의 근원과 배우려는 policy가 동일한 경우
Off-policy: experience sample의 근원과 배우려는 policy가 다른 경우
Action-value function을 이용하는 것의 장점
- state-value function을 사용하여 policy improvement를 하는 경우에는 MDP 가 필요하지만 action-value function을 사용하면 그렇지 않다.
Exploration
-
이 방법은 확률로 아무 액션이나 취하고 확률로 greedy action을 취하는 방식을 의미하는데 이렇게 하는 이유는 greedy exploration의 반복으로 local optimal에 빠지는 가능성을 배제하기 위함이다.
윗항에도 이 있는 이유는 랜덤하게 고른 action이 optimal 한 경우도 포함하기 위함이다 -
greedy 하게 고른 policy 가 state-value function을 증가시킴을 증명하기 위해서는 아래와 같은 수식이 필요하다.
위에서 보인 q가 보다 작음은 chap 2의 policy improvement 부분을 보며 따라갈 수 있고 위의 결과로부터 임을 알 수 있다.
중간 과정에서 부등호가 성립하는 이유는 위의 정의 과정에서 일반적인 a에 대해 임을 이용해 보인 것이다.GLIE (Greedy in Limit with Infinite Exploration)
-
GLIE를 만족시키기 위해서는 두가지 조건이 필요하다
모든 state와 action에 대한 조합을 충분히 방문한다는 것,
policy는 greedy policy로 수렴해야 한다는 것
우리가 공부한 Greedy가 위 조건을 만족시키기 위해서는 이 회차를 거듭할수록 0으로 수렴해야 한다. (ex)
위와 같이 탄생한 방법이 GLIE Monte-Carlo 방식이며 아래의 슬라이드와 같다.

TD를 사용하는 방법
-
위의 과정은 policy evaluation에 대해 MC 방법을, policy improvement에 대해 방법을 적용하고 있다.
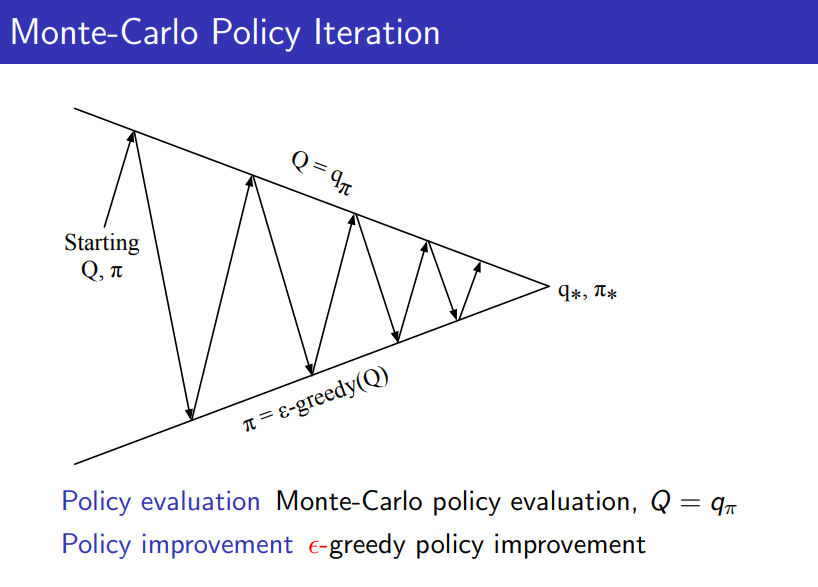
하지만 lower variance, Imcomplete sequence 같은 TD의 장점으로 인해 policy evalution 단계에서 MC 대신 TD를 적용해보는 방법도 생각해볼 수 있다. -
이를 SARSA 라고 하며 update 방식과 SARSA 라고 불리는 이유는 아래의 그림과 pseudo-code를 보면 이해할 수 있다.
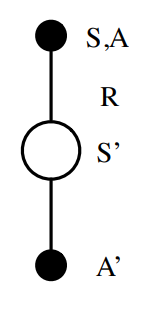
Q(s,a) 초기화
for each episode:
S 초기화
policy Q로 S에서 A유도
for each step (in episode):
Action A 에서 나온 R 과 S' 관찰
policy Q로 S'에서 A'유도
Q(S,A) <- Q(S,A) + a[R+rQ(S',A')-Q(S,A)]
S <- S', A <- A'
break if S is terminalSALSA가 converge하는 조건
- 다음과 같은 조건에서 optimal action-value function으로 수렴한다.
- sequence 가 GLIE sequence 일 것
- step-size 가 Robbins-Monro 시퀀스일 것
이 두 식은 각각 step size가 무한히 긴 큐에 다다를 정도의 성질을 가지면서도 두 번째 식으로부터 수렴해야 하다는 조건을 의미한다.
Practice에서 Robbins-Monro 에 대한 조건은 무시되어도 동작하며 GLIE 조건도 무시해도 되기도 한다.
SALSA n-step, Forward, Backward
- chap 3에서 배운 것과 같이 SALSA는 TD 베이스이므로 n-step 적용이 가능하고 terminate 직전까지 가면 MC와 동일해진다.(이미 배운 내용) 수식으로는 아래와 같다.

- forward와 backward에 대해서도 이전 장의 prediction에서 했던 것과 마찬가지로 backward에 eligibility trace를 곱하면 forward와 같은 효과를 낼 수 있으며 이는 practical 한 부분에서 도움이 된다.
앞선 장에서 다룬 내용들과 동일하기 때문에 수식 입력 대신 슬라이드로 대체한다.



Off-policy Learning
- 다른 policy를 따르면서 현재 target policy의 state, action-value function을 evaluate하는 방식을 말한다.
- 이 방식의 중요성은
- 다른 Agent로부터 학습가능
- 예전 policy 로부터 얻은 experience들을 재사용 가능
- Exploratory policy들을 따르면서 optimal policy에 대해 학습
- One policy를 따르면서 multiple policies를 배우기 가능
- 이를 처리하기 위한 2가지 mechanism에 대해 배운다.
Importance Sampling
-
같은 함수에 대해 다른 distribution에서 기댓값을 구하기 위해서는 아래와 같은 조작이 필요하다.
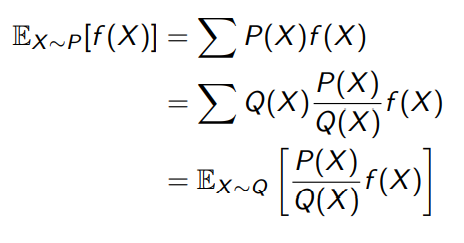
위와 같은 성질을 이용하여 MC 에서 value function을 업데이트 하기 위해서는 아래와 같은 목표값 설정이 필요하다

여기서 우리는 distribution에서 value function을 업데이트 하는 것이므로 위와 같은 처리가 필요함을 알 수 있다.
하지만 위의 방법은 너무 높은 variance로 인해 계산값에 큰 의미를 갖지 않는다. -
이전 강의에서 배운 것과 같이 TD의 장점 중 하나는 variance가 낮다는 것인데 이를 통해 MC를 대체할 TD 를 적용했을 때 어떤 식을 따라야 할지는 아래 수식과 같다.
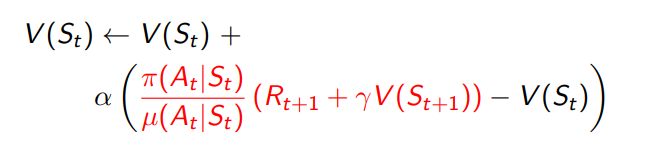
마찬가지로 distribution에서 Expectation으로 이뤄져 있는 value function을 업데이트 하고 있는 중이기 때문에 위와 같은 식이 필요하다.
MC 방법보다 작은 variance를 갖는다.
Q Learning
- Q Learning 에서 우리는 behaviour policy를 통해 Return을 얻지만 alternative action에 대해 Q 함수를 업데이트 한다.
일 때 Q 함수는 아래와 같이 update 된다.
Q Learning Control
-
Control 을 하고자 할 때는 behaviour 와 target policy를 improve 하려 하고 각각의 조건은 아래와 같다.

-
Behaviour policy와 target policy는 각각 greedy와 -greedy 하며 그러므로 Q 함수 update 과정의 target이 다음과 같이 간단히 표현된다.
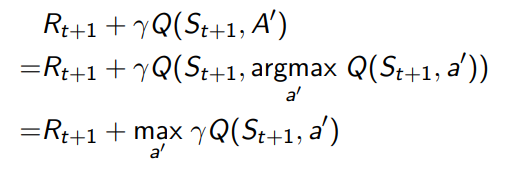
최종적인 과정은 아래와 같이 도표와 수식으로 표현된다.
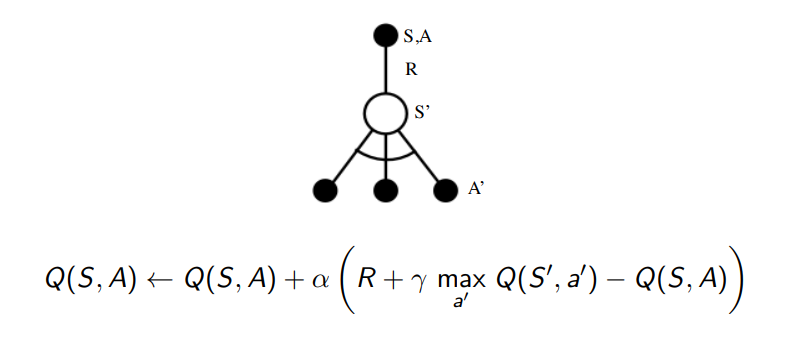
내용정리
- 지금까지 배운 내용을 정리하면 아래 표와 같다.
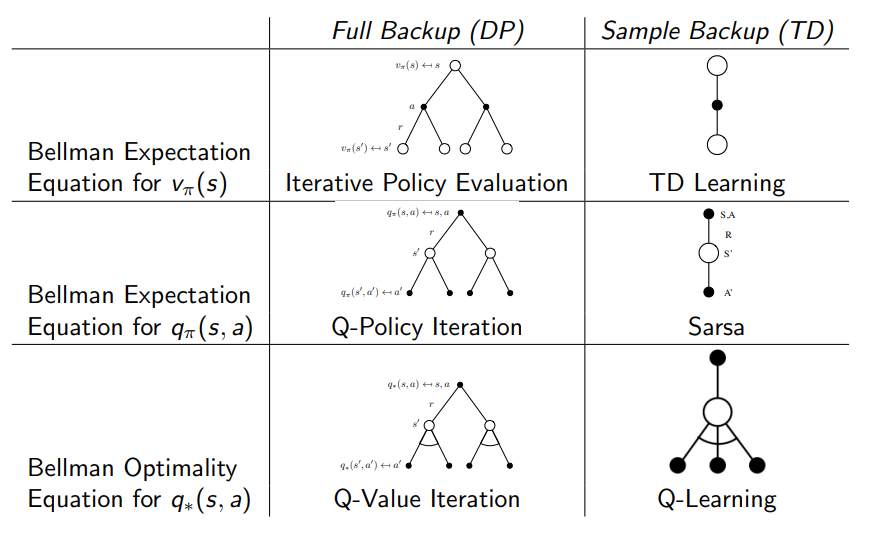
v를 구하는데 TD는 DP의 한 episode만 sampling 하여 결과를 얻음을 알 수 있고 q를 구하기 위한 SARSA 와 optimal q를 구하기 위한 Q-learning에 대한 개념을 정리할 수 있다.

수식적으로는 다음과 같으며 Q-Learning을 배우기 위해 DP 과정을 배웠음을 알 수 있으며 왼쪽 식들의 step size alpha의 의미는 target 방향으로 특정 값만큼 이동함을 의미한다.
