QR-DQN Distributional Reinforcement Learning with Quantile Regression
Introduction
이 논문의 등장배경은 앞선 C51 방식이 Wasserstein distance의 contraction을 증명해놓고 결국 SGD 방식을 이 distance에 사용할 방식을 찾지 못해 KL divergence(== cross entropy)를 사용한 것을 보완해 end-to-end 로 Wasserstein distance를 사용할 수 있는 framework를 개발했다.
- C51과의 차이점
1) C51 에서는 고정된 support를 정해놓고 그에 알맞는 확률값을 배우는 방식으로 이뤄졌었지만 여기서는 ‘Transpose’ 시켜 동일한 확률을 N개의 support 에 대해 정하는 방식으로 학습이 이뤄진다.
2) Wasserstein distance를 사용할 방법으로 quantile regression 의 도입을 고려한다.
결과)
우회법인 heuristic approximation을 도입한 c51보다 좋은 성능을 보였다.
background
Wasserstein distance가 선호되는 이유?
1) Underlying metric을 우선시 하는 성질이 돋보임
2) Outcome event 들에 대해 Probability와 동시에 distance를 고려한다 → outcome 들 사이의 underlying similarity 가 정확히 일치하는 것보다 중요한 경우 유용하게 사용된다.
Theorem 1 에서 Wasserstein 이 SGD 못하는 이유를 알려주는데 정밀하게 보는게 좋을 거 같음
본문
여기서는 quantile 방식을 사용함 → ex) [0, 0.25, 0.5, 0.75, 1.0] : 그렇기 때문에 일정 확률을 갖는 support에 대해 추정하는 형태로 학습이 이뤄지는 것임
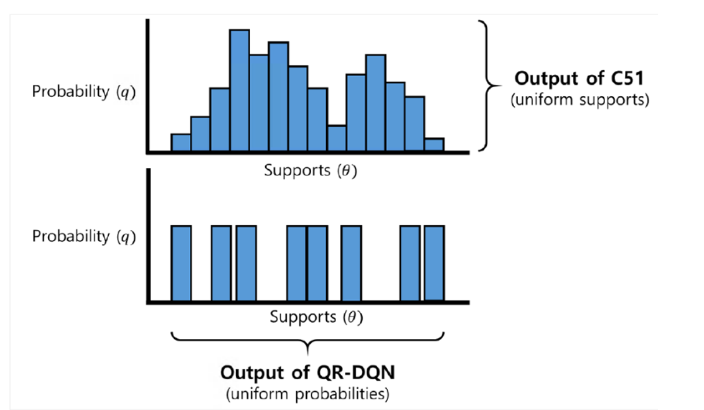
그림으로 보면 위와 같은 차이점이 있고 C51의 hyperparameter는 (V_min, V_max)이고 네트워크의 output은 y축인 확률인 반면 QR-DQN 의 방식은 y축이 정해져 있기 때문에 hyperparameter로 support의 개수를 정한다면 네트워크의 output으로 x축을 계산해야 한다.
위와 같이 x축인 support를 찾는 구조는 아래와 같은
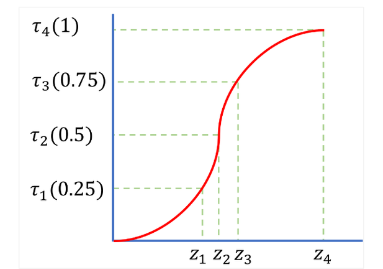
quantile(N=4) 인 그래프에서 z 값들을 찾는 것과 동일하며 (y축의 일정한 증가는 같은 확률 분포를 의미) 이러한 구조를 택한 이유는 end-to-end Wasserstein distance를 사용하기 위함이다.
다시 정의로 돌아가보자면
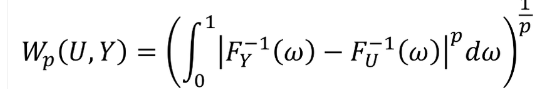
과 같고 역함수의 차이를 최소로 만드는 것이므로 이는 quantile regression 의 목적과 일맥상통하다고 할 수 있다.
Quantile regression 과 Wasserstein distance가 단조관계를 갖기 시작하므로 이전 논문에서 증명한 Wasserstein 의 contraction 성질을 사용할 수 있게 된다.
Quantile Number N
이 때 주의할 점은 확률을 직접 1/N로 사용하는 것이 아닌 아래와 같은 quantile midpoint를 사용한다는 점이다.
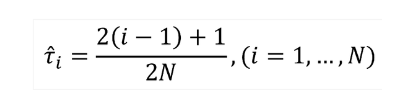
이는 아래와 같은 식을 최소로 만드는
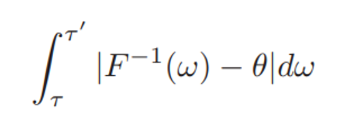
Theta의 값은 아래와 같은 조건을 만족해야 하기 때문이다.
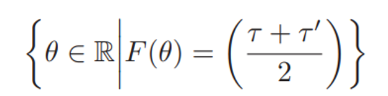
x축에 오게 될 theta 의 y축에 대응하는 값은 원래 quantile의 mid point이기 때문이다.
이에 대한 증명은 먼저
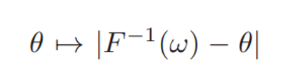
이 값이 convex 함을 보이면서 시작하는데 theta 가 F^-1 보다 작을 경우 gradient는 -1, theta 가 F^-1 보다 클 경우 gradient는 1이기 때문에 아래로 볼록한 convex 한 성질을 갖는다.
그러므로 아래와 같이
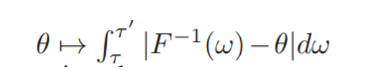
위에 대한 적분식도 theta에 대해 convex 하며 위의 식의 theta 에 대한 gradient은 아래와 같다.
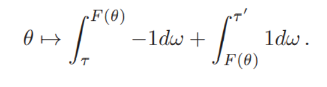
Gradient 를 0으로 만드는 값은
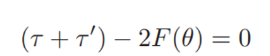
위의 식을 만족하기 때문에 원하던 대로 두 quantile 사이의 값이 부분적인 Wasserstein distance를 최소로 만듦을 알 수 있다.
Quantile Regression Loss
- 두가지 목적을 갖고 있음
1) Target value distribution과 예측된 value distribution 간 support 차이를 줄이는 방향으로 이동
2) 낮은 quantile 에 대해서는 낮은 support 값, 높은 quantile에 대해서는 높은 support 값을 가져야 함 → 반대로 된다면 단조 증가해야하는 CDF의 성질에 위반됨을 알 수 있음
수식은 아래와 같이 정의됨
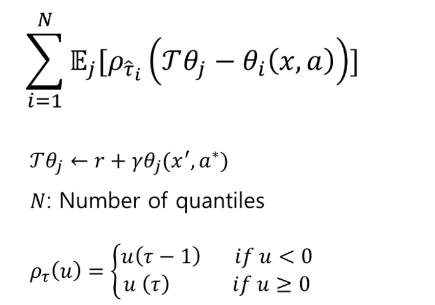
i는 quantile 의 index를 의미하며 j는 theta를 추측하는 network 의 expectation을 위하기 위한 index를 나타낸다.
이 loss 는 2) 번의 목적을 달성하기 위해 위와 같은 rho 함수를 도입하고 있는데 tau 가 작은데 높은 support 를 예측한 경우의 패널티를 크게 주기 위해 rho 의 case 1을, tau 가 큰데 작은 support를 예측할 경우의 패널티를 크게 주기 위해 rho의 case 2를 만들었다.
rho 함수는 unit function 이 아님에 주의!
논문에서는 아래와 같은 수식으로 소개되어있다.
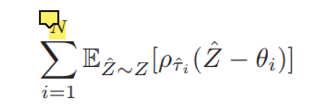
Quantile Huber Loss
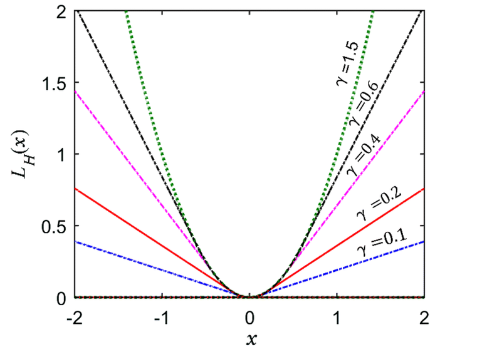
Quantile regression loss를 그대로 사용할 경우 불연속점에 대해 미분 불가능한 현상이 발생하므로 Huber loss를 추가해 주어 연속적으로 만들어준다.
미분 불가능한 현상은 사이트에 설명되어 있어 참조하면 된다.
Distributional Reinforcement Learning with Quantile Regression
Huber function의 모습은 아래와 같다.
기존 quantile loss의 rho 함수 부분만 아래와 같이 변화하게 된다.
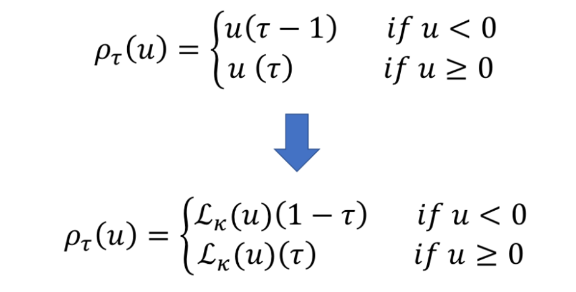
Overall

전체적인 알고리즘은 위와 같다. C51 방식과 비교해 네트워크 output이 transpose 되었지만 Q를 구하는 방식은 동일하며 최소화 하려는 loss 는 Quantile Huber Loss 이다.
