Deep Deterministic Policy Gradient(DDPG)

Intro

DQN과 같이 discretized action에 특화된 방식을 continous 한 task에 적용할 경우 차원의 저주에 빠지게 된다.

ex) 각 joint에 대해 세가지 action을 취할 수 있는 robot의 control 문제에서 joint 의 수에 따라 3의 지수승으로 action 집합이 증가한다.

→ 이렇게 넓어진 action state를 모두 탐색하는 것은 불가능할 뿐만 아니라 이러한 discretization은 정보 손실을 초래한다.

이에 따라 DQN의 key idea인 replay-buffer와 target Q network 개념을 사용해 actor-critic 방식의 NN을 사용한 function approximation을 적용하고자 한다.

---

Background

우리는 determinstic 한 policy를 가정하며 이는 state가 주어지면 바로 이에 대응하는 action이 100% 확률로 존재함을 의미한다.

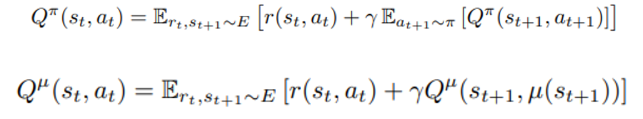
위의 식은 stochastic policy, 아래는 deterministic policy를 의미하며 expectation이 하나 벗겨진 것을 확인할 수 있고 $a_{t+1} = \mu (s_{t+1})$로 대체된 것을 확인할 수 있다.

---

본문

Continous task에서는 Q-learning을 사용할 수 없다

→ greedy policy를 적용하기 위해서 (s,a)에 대한 최대 Q 값을 찾아야 하는데 매 step 마다 optimization 과정이 필요하기 때문이다.

Actor는 $\theta^{\mu}$라는 파라미터를 통해 deterministic 하게 state에 맞춰 action을 결정하며 아래와 같이 gradient로 objective function을 최대화 시키려한다.

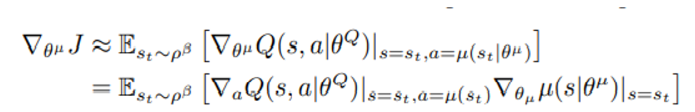
밑의 줄은 chain-rule을 적용한 모습이다.

(이 부분이 코드에서는 어떻게 구현?)

Critic은 다음과 같은 loss function을 최소화 시키는 방향으로 parameter들이 학습된다.

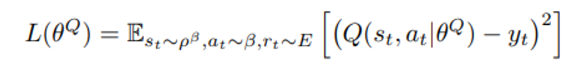
Function approximation 에 Neural Network 를 사용할 때의 지켜야할 점

1) sample 이 IID(Independent and Identically Distributed) 일 것 → replay buffer로 해결

2) mini-batch로 학습시키는 구조를 만들 것

DQN에서 제시된 Replay buffer를 통해 이러한 문제를 해결가능 (특히 (1)의 문제를 uncorrelated transition의 조합으로 해결)

DQN의 target Q와의 차이

• learning 의 stability를 높이기 위해 soft target update를 진행

$\theta' = \tau \theta + (1-\tau)\theta'$다

• 서로다른 task에 대해 observation의 physical unit이 다를경우 매번 hyper-parameter를 바꿔줘야하는 문제가 발생하므로 batch normalization 을 도입 → state input에 대해, deterministic policy network 에 대해, Q network의 action input 전 모든 layer에 대해

Exploration을 시키기 위한 조치

원래 deterministic policy에 아래와 같은 noise를 더해 진행

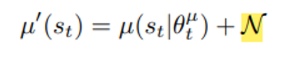
전체 알고리즘

빨간색으로 표시한 부분을 보면 u에 의한 선택된 action에 의해 한 step을 진행 후 N transition을 가져와 훈련하고 있음을 알 수 있다. (1:N 구조)