What is log likelihood + L2 Norm 정당화

What is Log Likelihood

least square regression 상황 하에서 i 번째 정보에 대해 다음과 같은 식을 생각할 수 있다.
$y^{(i)} = \theta^Tx^{(i)} + \epsilon^{(i)}$
만약 $\epsilon$가 normal distribution 을 따른다고 하면 위의 수식에 의해 $y^{(i)} - \theta^Tx^{(i)}$ 항이 같은 분포를 따른다고 할 수 있다.
그렇다면 이러한 분포를 $p(y^{(i)}|x^{(i)};\theta)$ 라고 칭할 수 있고 이를 likelihood function $L(\theta)$ 로 정의한다.
그렇다면 모든 정보 i가 independent 하다고 가정할 경우 전체 Likelihood는 각 likelihood 의 곱으로 나타낼 수 있으며 식으로는 다음과 같다.

$L(\theta) = \prod_{i=1}^m p(y^{(i)}|x^{(i)};\theta)$

각 정보에 대해 y가 맞을 확률을 최대로 하는 것이 목표이기 때문에 전체 곱의 결과가 최대가 되길 원하며 곱셈을 덧셈으로 치환하기 위해 양변에 log를 취해 log likelihood의 정의를 얻는다.

L2 Norm의 정당화

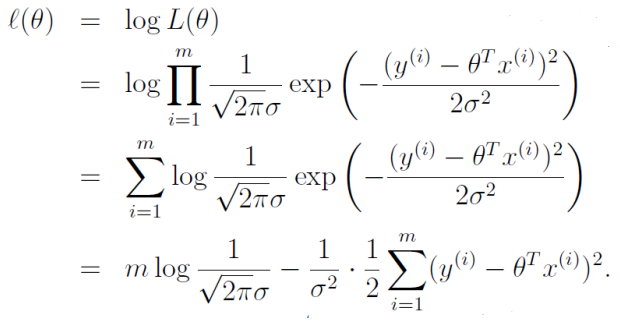
위의 결과는 $\epsilon$의 정규분포를 가정했기 때문에 유도된 결과이며 마지막 항으로부터 log likelihood를 최대로 만들기 위해서는 L2 Norm이 최소값을 가져야 함을 알 수 있다.