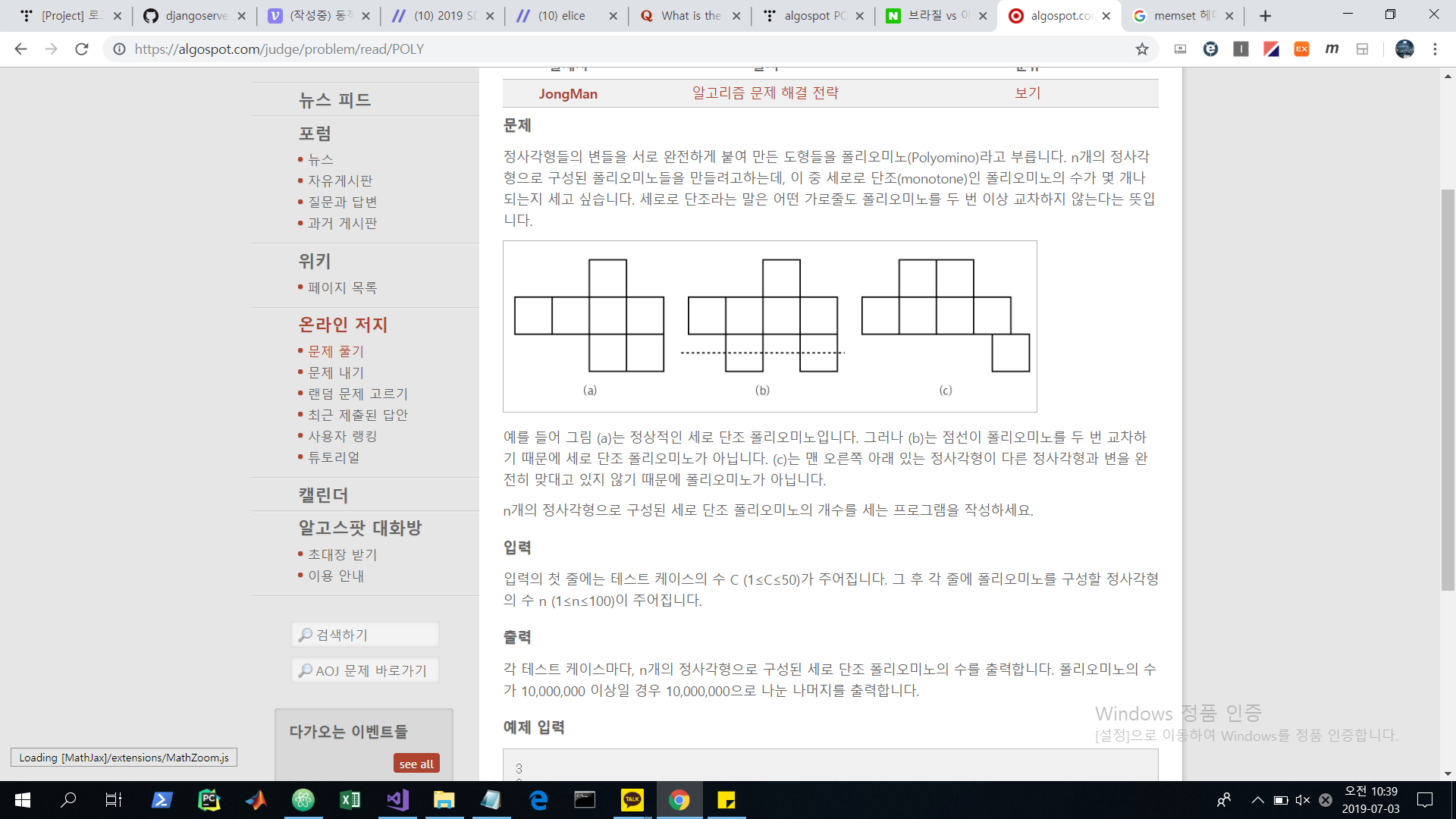
문제 파악

DP를 사용하기에 앞서 완전 탐색으로 접근하기 위해서 폴리오미노의 경우의 수를 따질 수 있는 방법을 생각해 보았다. 각 도형을 한 줄씩 나눠 개수를 더하는 방식을 생각해 보았는데, 이 과정에서 발생하는 중복과 개수별로 조합했을 때 발생하는 합친 도형의 개수가 달라져서 이 부분에서 처리를 어떻게 할지 생각해 낼 수가 없었다.

올바른 풀이

완전탐색

폴리오미노의 개수를 세기 위한 핵심 아이디어는 첫 번째 줄의 블록 개수 부터 따지는 것이다. 첫 번째 블록에 오는 상자의 개수로 n개로 만들 수 있는 도형의 종류를 나눌 수 있다. 이 분류는 모든 경우의 수를 나눌 수 있으며, 서로 겹치는 일도 없다.
n개로 만들 수 있는 폴리오미노의 첫 줄에 x개의 블록이 왔다고 하면, 둘 째줄 부터 끝까지 n-x개의 도형을 사용해야 한다. 따라서 이를 점화식으로 나타내면, 아래와 같은 식이 된다.

poly(n, x) = poly(n-x, 1부터 n-x까지) 

조합 만들기

첫 번째 줄에 오게될 블록의 수를 결정하게 된다고 해서 모든 경우의 수를 바로 알 수 있는 것이 아니다. 첫 줄의 블록의 수와 두 번째 줄에 오게 될 블록의 수에 따라서 두 줄을 연결하는 경우의 수가 달라지게 된다.
몇 가지 예시를 그려보며 간단히 확인해 보면 첫 줄에 first개의 사각형이 오고, 두 번째 줄에 second개의 사각형이 온다고 가정하면, 둘을 잇는 경우의 수는 first+second-1임을 확인할 수 있다.

최종 점화식

지금까지의 아이디어를 통해 폴리오미노를 만드는 최종 점화식을 완성해보자. 두 번째 줄에 오는 블록의 수로 만들 수 있는 경우의 수에 첫 번째 줄과 잇는 경우의 수를 곱해 주어야 한다.

poly(n,first) = for second = 1부터 n-first까지{
				sum+=(second+first-1)*poly(n-first,second)
                }

첫 줄의 블록의 개수를 결정하고 두 번째 줄의 블록의 개수의 범위 1부터 n-first까지 하나씩 따져줘 가면서 첫 줄과 잇는 경우의 수를 곱해주면 모든 경우의 수를 구할 수 있다.

느낀점

결국 이 문제의 핵심 아이디어는 폴리오미노를 완전 탐색하는 방식을 어떻게 일반화 할 것이냐이다. 모든 경우의 수를 따질 수 있고, 종류 별로 겹치지 않는 분류법을 확실하게 생각해 내는 것이 중요하다. 이 문제에서는 첫 줄을 기준으로 생각하는 것이 분류법의 핵심 아이디어였다. 무수한 형태의 도형이라고 하더라도 첫 줄이라는 모든 도형이 공유하고 있는 부분에 대해서만 생각의 범위를 좁히면 도형을 분류하는 것이 가능해진다.