문제 파악
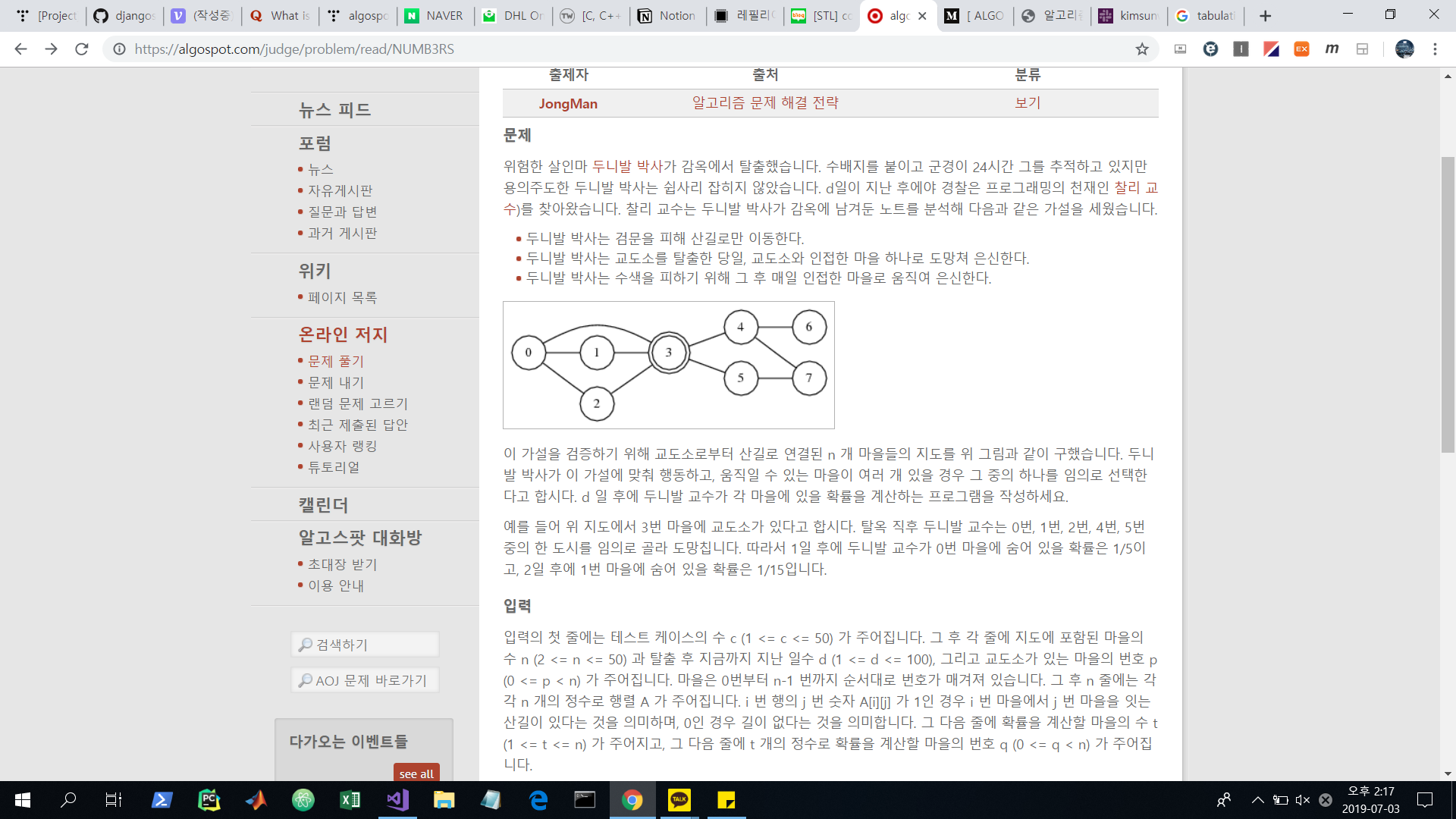
문제를 이해하고, 각 days에 노드들의 확률이 서로 어떤 연관이 있음을 명확히 알 수 있었다. 각 노드들의 해당 날짜의 확률은 그 전 날 인접 노드의 확률로부터 얻어질 수 있음을 느낄 수 있었다.
따라서 이러한 직관을 바탕으로 days에 따른 노드들의 관계를 정의해 보았다.
해당 날짜에서 특정 노드의 확률은 그 전날 인접 노드들의 확률을 그 인접 노드의 인접 노드 개수로 나눈 값들의 합이다. 즉 두니발 박사가 특정 노드로 넘어 오기 위해서는 반드시 그 전 날 인접한 노드에 있어야 하는데, 두니발 박사가 반드시 특정 노드로 넘어오는 것이 아니라 현재 갈 수 있는 노드 중 하나로 오는 것이기 때문에 이와 같은 관계가 성립하는 것이다.
이러한 이해를 바탕으로 코드를 구현해 정답을 맞출 수 있었다. 그 과정에서 약간의 시간이 소요된 부분은 C++의 memset 함수는 바이트 단위에서 값을 변경해 주는 기능을 하기 때문에, integer에 대해서는 배열의 모든 값에 -1을 쉽게 채울 수 있지만 double형 배열에 대해서는 무작정 채울 수 없다는 점이었다.
문제 풀이
위 문제는 크게 두 가지 방식으로 풀이가 나뉜다
앞에서 부터 보는 경우(각 도시에서 부터 따지는 경우)
기저 사례가 d==구하고자 하는 날짜로 첫 날부터 목표 날까지 올라가면서 재귀 호출한다. 특정 노드에 대해서만 값이 구해지므로, 구하고자 하는 노드의 수 만큼 시간 복잡도가 증가하므로 더 비효율적이다. 기저 사례가 목표로 하는 노드에 따라서 달라지기 때문에 매번 memoization이 달라지게 되고, 캐시를 초기화 해줘야하기 때문에 구하고자 하는 도시 수 만큼 증가하는 것이다.
뒤에서 부터 보는 경우(출발 도시에서 부터 따지는 경우)
내가 푼 방식과 동일하다. 기저 사례가 d==0 또는 1 즉 주어진 날짜부터 첫 날까지 거슬러 올라가며 재귀 호출한다. 모든 노드에 대해서 값을 구할 수 있으므로 더 효율적이다. 기저 사례는 어떤 도시에 대한 값을 구하든, 동일하기 때문에 캐시를 초기화할 필요가 없다.
