1. 선형 회귀란 ?

선형 회귀(Linear Regression)이란 머신러닝 중 연속적인 숫자 값을 예측하고 싶을 때 사용하며 주어진 데이터를 가장 잘 설명하는 직선 하나를 찾는 것 이다.

• 독립 변수 (X) : 원인이 되는 데이터 ( ex. 공부 시간 )
• 종속 변수 (Y) : 결과가 되는 데이터 ( ex. 시험 성적 )
  선형 회귀는 이 X가 변할때 Y가 어떻게 변하는지 예측하는 모델을 만드는 과정이다.

2. 핵심 개념

2-1 . 가설 (Hypothesis)

우리가 찾으려는 직선은 다음 방정식으로 나타낼 수 있다.

이때 $W$는 가중치(Weight)이며 직선의 기울기 이며, $b$는 편향(bias), 즉 y절편이다.
머신 러닝의 목표는 주어진 데이터에 대해 가장 적절한 $W$와 $b$를 찾는 것이다.

2-2. 비용 함수 (Cost Function / Loss Function)

우리가 찾은 직선이 실제 데이터와 얼마나 차이가 나는지 오차를 계산하는 함수이다.
가장 대표적인 비용 함수는 평균 제곱 오차(Mean Squared Error, MSE)이다.

• 제곱을 하는 이유는 오차의 크기를 극대화하고, 음수 값을 없대기 위함이다.
• 우리의 목표는 이 $Cost$를 최소로 만드는 $W$와$b$를 찾는 것이다.

  해당 내용은 손실 함수 - L1 loss & L2 loss에서 잘 나와있습니다 :)

2-3. 경사 하강법 (Gradient Descent)

$Cost$를 최소화하는 $W$와$b$를 어떻게 찾을지에 대한 방법론 중 하나이다.
함수의 변화량을 이용하여 계수들 조정하는 방식으로, 함수가 줄어드는 방향으로 계수를 계속 갱신해 나간다.
우리는 함수가 한번에 얼마나 줄어들게 하는지를 결정하는 파라미터를 정해야하며 이를 학습률이라고 한다.
이때, 파라미터가 너무 작으면 최적화가 오래걸리고, 너무 크면 최솟값을 지나칠 수 있다.

경사하강법에 대한 포스트를 이어서 쓸 것이므로 해당 포스트에서 자세하게 공부해보자.

경사하강법에 대한 포스트 바로가기

3. Scikit-learn 을 이용한 선형 회귀

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression

# 1. 데이터 준비
num_point = 100

# 모델이 찾아내야 할 실제 정답
true_W = 3.5
true_b = 8.0

# X와 Y 데이터를 랜덤으로 생성
noise = np.random.randn(num_point,1)
X = 2 * np.random.rand(num_point,1)
Y = true_W * X + true_b + noise

# 2. 선형 회귀 모델 생성 및 학습
model = LinearRegression()
model.fit(X,Y)

# 결과 확인
predict_W = model.coef_[0][0]
predict_b = model.intercept_[0]

print(f"true W :{true_W}")
print(f"predict W : {predict_W:.2f}")
print("-" * 30)
print(f"true b : {true_b}")
print(f"predict b {predict_b:.2f}")

true W :3.5
predict W : 3.67
------------------------------
true b : 8.0
predict b 7.81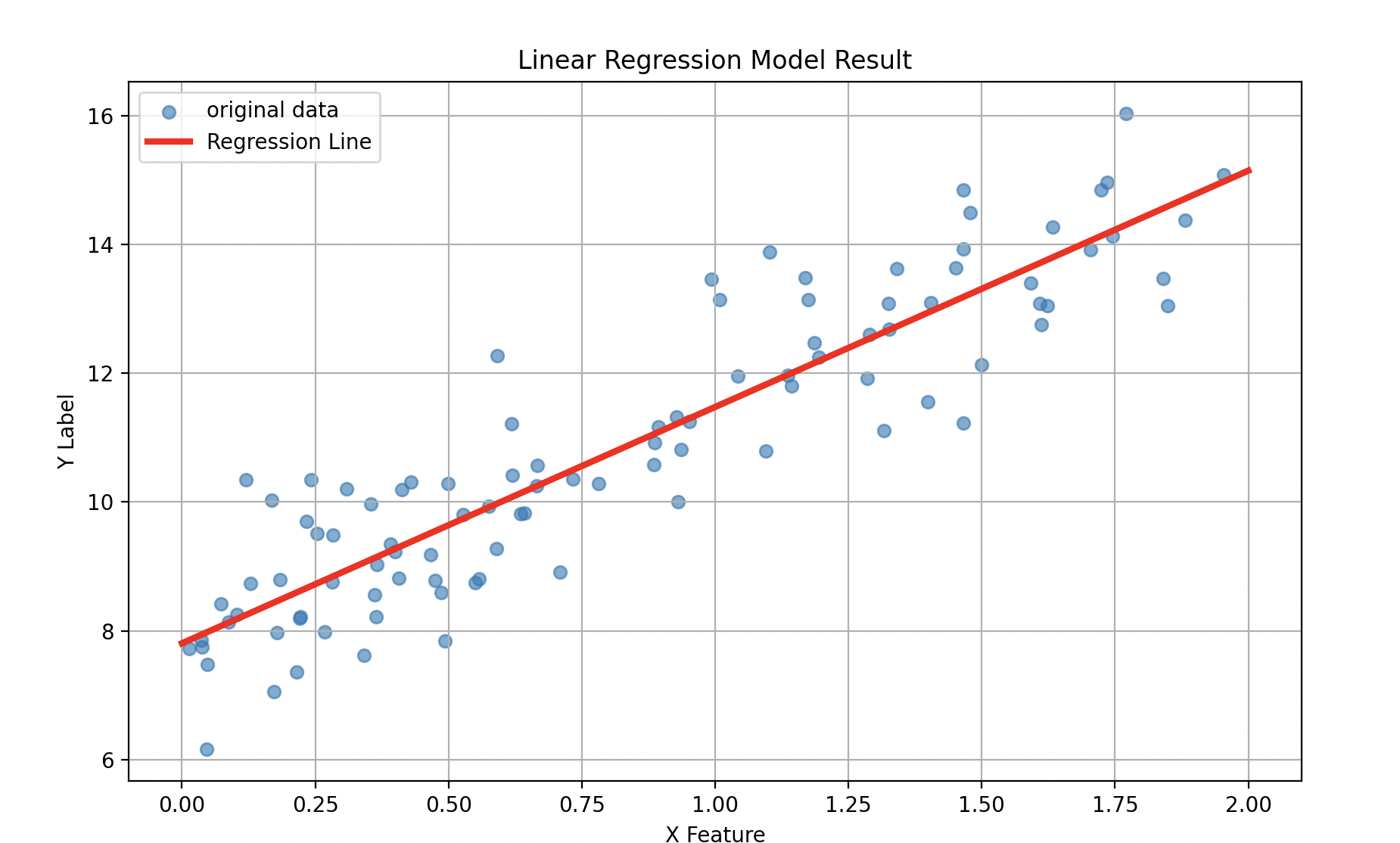

보이는 것과 같이 열심히 예측하는걸 볼 수 있다!
파이썬의 scikit-learn 라이브러리를 사용하면 Linear Regression() 메서드로 한줄로 선형 회귀를 할 수 있다.

• model.coef_에는 학습된 $W$가 저장되며 2차원 배열 형태로 저장된다.
  • 선형회귀는 여러 개의 특성 ($X$) 를 가질 수 있기때문에(다중 선형 회귀) scikit-learn는 각 특성에 대한 기울기가 별도로 계산되어 배열 형태로 저장된다.
• model.intercept_ 에는 학습된 편향 $b$가 저장된다.

다음 포스트에서 경사 하강법을 씹고 뜯고 맛보도록 하자....!