1. 경사 하강법

경사 하강법의 목표는 비용 함수(Cost Function)의 값을 최소로 만드는 파라미터를 찾는 것이다.

1-1. 준비

먼저 최적화 할 대상인 직선의 방정식을 정의하겠다.

그리고, 비용 함수는 MSE를 사용하여 정의하겠다 .

이때 우리가 찾아야할 파라미터는 $W$와$b$이다.

1-2. Gradient

비용함수 $J(W,b)$를 최소화하려면, 현재 파라미터 위치에서 비용이 가장 가파르게 감소하는 방향으로 $W$와$b$를 이동시켜야한다.
수학적으로 가장 가파른 방향은 기울기(Gradient)로 알 수 있으며, 이는 비용 함수를 각 파라미터로 편미분하여 구한다.

• $W$에 대한 편미분 ($W$의 영향력)

  $\frac{∂J}{∂W} = \frac{2}{m}\sum_{i=1}^{m}(H(x_i)-y_i)\times x_i$

• $b$에 대한 편미분 ($b$의 영향력)

  $\frac{∂J}{∂b} = \frac{2}{m}\sum_{i=1}^{m}(H(x_i)-y_i)$

1-3. Update

기울기(Gradient)를 구했다면, 이제 기울기의 반대방향으로 파라미터를 업데이트 한다. 이때, 얼마나 큰 간격으로 움직일지를 결정하는 것이 학습률(Learning Rate, $\alpha$) 이다.

경사 하강법은 이 과정을 수렴할 때까지 반복하는 것이다.

2. Numpy를 이용한 구현

import numpy as np
import matplotlib.pyplot as plt

# 1. 데이터 준비
num_point = 100

# 모델이 찾아내야 할 실제 정답
true_W = 3.5
true_b = 8.0

# X와 Y 데이터를 랜덤으로 생성
noise = np.random.randn(num_point,1)
X = 2 * np.random.rand(num_point,1)
Y = true_W * X + true_b + noise

# 2. 경사하강법 구현
learning_rate = 0.01 # 학습률
epochs = 1000 # 학습 반복 횟수

# 파라미터를 0으로 초기화
W = 0.0
b = 0.0

m = len(X)
cost_history = [] # 비용의 변화를 기록하기 위한 리스트

for epoch in range(epochs) :
    # 가설 계산
    predictions = W * X + b

    # 비용 계산
    cost = (1/m) * np.sum((predictions - Y) ** 2)
    cost_history.append(cost)

    # 기울기 계산
    W_gradient = (2/m) * np.sum((predictions - Y) * X)
    b_gradient = (2/m) * np.sum(predictions - Y)

    # 업데이트
    W = W - learning_rate * W_gradient
    b = b - learning_rate * b_gradient

# --- 3. 결과 출력 및 시각화 ---
print("--- 학습 완료 ---")
print(f"최종 예측 W: {W:.3f} (실제 값: {true_W})")
print(f"최종 예측 b: {b:.3f} (실제 값: {true_b})")

--- 학습 완료 ---
최종 예측 W: 3.629 (실제 값: 3.5)
최종 예측 b: 7.780 (실제 값: 8.0)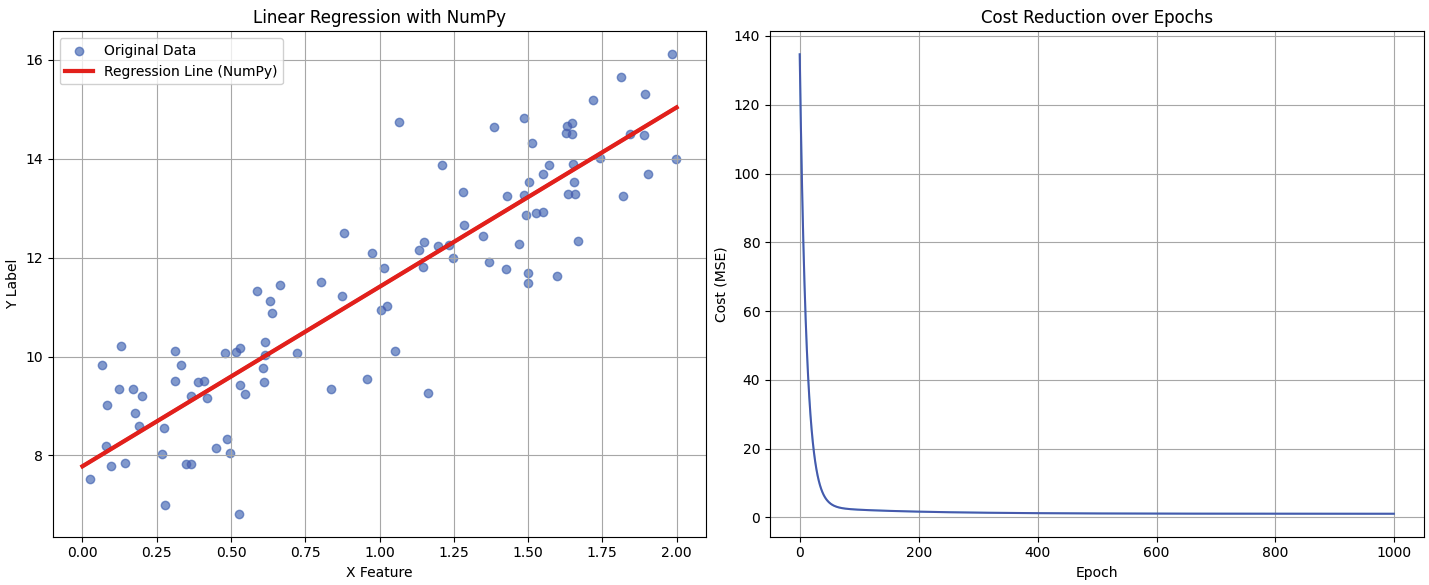

오른쪽 그래프는 학습이 진행됨에 따라 오차가 빠르게 감소하여 특정 값으로 수렴하는 전형적인 경사 하강법의 학습 곡선을 보여준다.