1. 계통수란?
계통수(Phylogenetic Tree) 란 생물학에서 여러 종(또는 개체군, 유전자 등)들이 진화 과정에서 어떻게 갈라져 나왔는지, 그들 사이의 진화적 관계와 유연관계를 Tree 형태로 나타낸 그림이다.
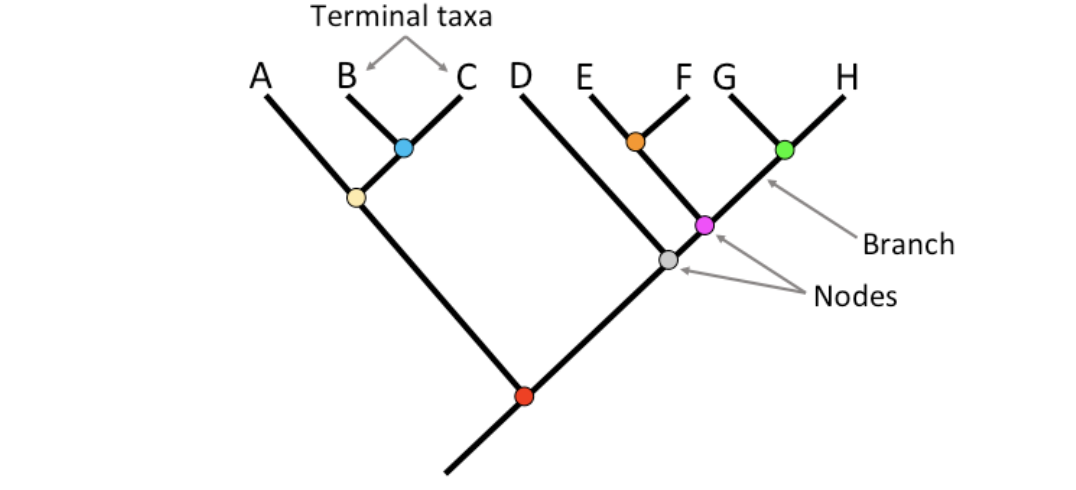
계통수의 구성요소
- Branch : 선으로 표현되며, 각 종이나 그룹 간의 진화적 경로를 나타낸다. branch의 길이는 진화적 시간이나 유전적 변화의 양을 의미하기도 한다.
- Node : 가지가 갈라지는 지점으로, 공통 조상을 의미한다. 해당 지점에서 새로운 종으로 분화가 일어났음을 의미한다.
- Leaf or Terminal : 현재 살아있는 종이나 분석 대상이 되는 특정 그룹을 나타낸다.
- Root : 계통수의 가장 시작점이 되는 부분으로, 모든 생명체의 가장 오래된 공통 조상을 의미한다. 뿌리가 있는 계통수를 유근 계통수(Rooted tree) 라고 한다.
계통수에 쓰이는 데이터
- 형태학적 데이터 : 생물의 겉모습, 해부학적 구조, 화석 기록 등 눈으로 관찰 가능한 특징들을 비교하여 분석한다. 전통적으로 많이 사용된 방식이다.
- 분자생물학적 데이터 : DNA, RNA 서열이나 단백질 아미노산 서열과 같은 유전 정보를 비교 분석한다. 현대 계통분류학에서는 이 데이터가 매우 중요하게 사용된다.
계통수의 중요성
- 생물 분류 : 생물을 진화적 관계에 따라 분류하는 역할을 한다.
- 진화 연구 : 특정 형질이 어떻게 진화했는지, 종 분화가 언제 어떻게 일어났는지 등을 연구하는 데 사용된다.
- 질병 연구 : 바이러스나 세균의 확산 경로를 추적하고 변이 과정을 이해하는데 활용된다.
- 생태학 및 보전 생물학 : 종의 다양성을 파악하고 보전 우선순위를 정하는데 도움을 준다.
2. Neignbor-Joining(NJ) 알고리즘
NJ 알고리즘(Neignbor-Joining) 은. ㅕ러 종 간의 유전적 또는 형태적 거리 를 바탕으로 계통수를 구축하는 거리 기반(Distance-based) 방법이다.
이 알고리즘의 핵심 아이디어는 전체 게통수의 길이를 최소화하는 방향으로 가장 가까운 이웃(Neighbor)을 순차적으로 묶어 나가는 것이다. 단순히 거리가 가장 가까운 쌍을 묶는 것이 아니라, 전체 Tree의 균형을 고려하여 최적의 쌍을 찾는다는 점에서 다른 군집화 방법(ex. UPGMA)과 차이가 있다.
NJ 알고리즘의 단계별 과정
1. 거리 행렬(Distance Matrix) 계산
분석하고자 하는 모든 종들 간의 거리(유전적 차이 등)를 계산하여 행렬 형태로 만든다.
| A | B | C | D | |
|---|---|---|---|---|
| A | 0 | 5 | 9 | 9 |
| B | 5 | 0 | 10 | 10 |
| C | 9 | 10 | 0 | 8 |
| D | 9 | 10 | 8 | 0 |
2. Q - 행렬 (Q-Matrix) 계산
단순히 두 종 사이의 거리만 보는 것이 아니라, 다른 모든 종들과의 평균 거리를 보정하여 '진짜 이웃'을 찾기 위한 Q-value를 계산한다.
- : 현재 남아있는 종의 수
- : 종 와 종 사이의 거리
- : 종 에서 다른 모든 종까지의 거리의 합
3. 가장 가까운 이웃 찾기
계산된 Q-matrix에서 가장 작은 값을 갖는 쌍(pair)을 찾는다.
이 쌍은 현재 단계에서 가장 가까운 '이웃'으로 간주된다.
4. 새로운 마디(Node) 생성 및 가지 길이 계산
3단계에서 찾은 이웃을 묶어 새로운 내부 마디(Internal node)를 생성한다.
그리고 각 이웃에서 새로운 마디까지의 Branch 길이를 계산한다.
5. 업데이트
이제 묶인 두 종은 하나의 새로운 마디로 취급된다.
기존 거리 행렬에서 A와B를 제거하고, 새로운 마디를 추가한다.
남아있는 다른 종들과 새로운 마디 사이의 거리를 다시 계산하여 행렬을 업데이트한다.
6. 반복
종의 개수가 3개가 남을 때 까지 반복을 하며, 마지막 남은 3개의 마디는 하나의 뿌리없는 트리(Unrooted Tree)로 연결되어 계통수가 최종적으로 완성된다.
NJ 알고리즘의 장단점
장점
- 빠른 속도
- 분자 시계 불필요 : 진화 속도가 종마다 달라도 적용할 수 있어, 모든 가지의 길이가 같아야한다는 '분자 시계(molecular clock)'가정을 필요로 하지 않는다.
- 대부분의 경우에서 합리적이고 정확한 계통수를 생성한다.
단점
- 하나의 결과만 생성한다.
- Long-Branch Attraction(LBA) : 진화적으로 멀리 떨어져있지만 진화 속도가 매우 빨라 유전적 변화가 많이 축적된 두 종을 실수로 가깝게 묶는 현상이 발생할 수 있다.
- Unrooted Tree 생성 : 종들 간의 상대적인 관계만을 보여줄뿐, 어디가 가장 오래된 공통 조상(Root)인지는 알 수 없다.
3. Python으로 계통수 만들기
우선 먼저 데이터를 가져와보자.
예제를 위해 나는 가상의 데이터를 가져왔다. 실제 데이터가 아님에 주의바란다.
아래 내용은 사람, 침팬지, 쥐, 닭의 미토콘드리아 유전자(Cytochrome B)일부의 데이터이다.
sequences.fasta 중
>Human
ATGGCCCCAAATCTCATCATCATCAACAACTTCCTGATCTGCTCCGCCACCCAA
GACACCTACTTCGCCTTCATCATAGCCGCTATCTCCACCGCAACAGGA
>Chimpanzee
ATGGCCCCAAATCTCGTCATCATCAACAACTTCCTGATCTGCTCCGCCACCCAA
GACACCTACTTCGCCTTCATCATAGCCGCTATCTCCACCGCAACAGGA
>Mouse
ATGGCCCCAAACCTAGTCGTCTTCAACAATTTTCTGATCTGCTCCGCCACCCAA
GGCTCCTACTTCGCCTTCATCATCGCCGCCATTTCCACCGCCACCGGC
>Chicken
ATGGCCTCAAACCTAGTCGTCATCAACAATTTCTTGATTTGCTCCGTCATCCAA
GGCTCCCCCCACGCCTTCGTCGTCGCCGCCATCTCCACCACCACCGGG그리고 다음 sequences.fasta파일을 clustalo를 활용하여 MSA처리 하겠다.
import subprocess
clustalw_exe = "/opt/homebrew/bin/clustalo"
input_file = "sequences.fasta"
cmd = [clustalw_exe, f"-INFILE={input_file}"]
try:
subprocess.run(cmd, check=True)
print(f"ClustalW 실행 완료! {input_file}.aln 파일과 {input_file}.dnd 파일이 생성되었을 것입니다.")
except FileNotFoundError:
print(f"오류: '{clustalw_exe}' 파일을 찾을 수 없습니다. 경로를 다시 확인해주세요.")
except subprocess.CalledProcessError as e:
print(f"ClustalW 실행 중 오류가 발생했습니다: {e}")clustal.aln 중...
CLUSTAL O(1.2.4) multiple sequence alignment
Human ATGGCCCCAAATCTCATCATCATCAACAACTTCCTGATCTGCTCCGCCACCCAAGACACC
Chimpanzee ATGGCCCCAAATCTCGTCATCATCAACAACTTCCTGATCTGCTCCGCCACCCAAGACACC
Mouse ATGGCCCCAAACCTAGTCGTCTTCAACAATTTTCTGATCTGCTCCGCCACCCAAGGCTCC
Chicken ATGGCCTCAAACCTAGTCGTCATCAACAATTTCTTGATTTGCTCCGTCATCCAAGGCTCC
****** **** ** ** ** ******* ** **** ******* ** ***** * **
Human TACTTCGCCTTCATCATAGCCGCTATCTCCACCGCAACAGGA
Chimpanzee TACTTCGCCTTCATCATAGCCGCTATCTCCACCGCAACAGGA
Mouse TACTTCGCCTTCATCATCGCCGCCATTTCCACCGCCACCGGC
Chicken CCCCACGCCTTCGTCGTCGCCGCCATCTCCACCACCACCGGG
* ******* ** * ***** ** ****** * ** ** 그리고, 이 정렬된 데이터를 가지고 계통수를 그려보자!
import matplotlib.pyplot as plt
from Bio import AlignIO, Phylo
from Bio.Phylo.TreeConstruction import DistanceCalculator, DistanceTreeConstructor
alignment_file = "clustal.aln"
print(f"'{alignment_file}' 파일을 읽어 계통수를 생성합니다...")
# 1. 정렬 파일 읽기
try:
aln = AlignIO.read(alignment_file, 'clustal')
except FileNotFoundError:
print(f"오류: '{alignment_file}' 파일을 찾을 수 없습니다. 파일 이름을 확인해주세요.")
exit()
# 2. 거리 행렬(Distance Matrix) 계산
# 'identity' 모델은 서열이 얼마나 다른지를 기준으로 거리를 계산합니다.
calculator = DistanceCalculator('identity')
dm = calculator.get_distance(aln)
# 3. 계통수 구축 (Neighbor-Joining 알고리즘 사용)
constructor = DistanceTreeConstructor(calculator)
tree = constructor.nj(dm) # nj() 메서드가 Neighbor-Joining을 수행합니다.
# 뿌리(root)를 가장 긴 가지의 중간 지점으로 설정하여 보기 좋게 만듭니다.
tree.root_at_midpoint()
# 4. 계통수 시각화
print("계통수 생성이 완료되었습니다. 이제 그림으로 표시합니다.")
# Matplotlib
fig = plt.figure(figsize=(10, 6), dpi=100)
axes = fig.add_subplot(1, 1, 1)
Phylo.draw(tree, axes=axes, do_show=False) # do_show=False로 설정 후
# 보기 좋게 레이아웃 조정 및 제목 추가
plt.title("Phylogenetic Tree (Neighbor-Joining)")
plt.xlabel("Evolutionary Distance")
plt.ylabel("Taxa")
plt.show()4. 데이터 분석하기
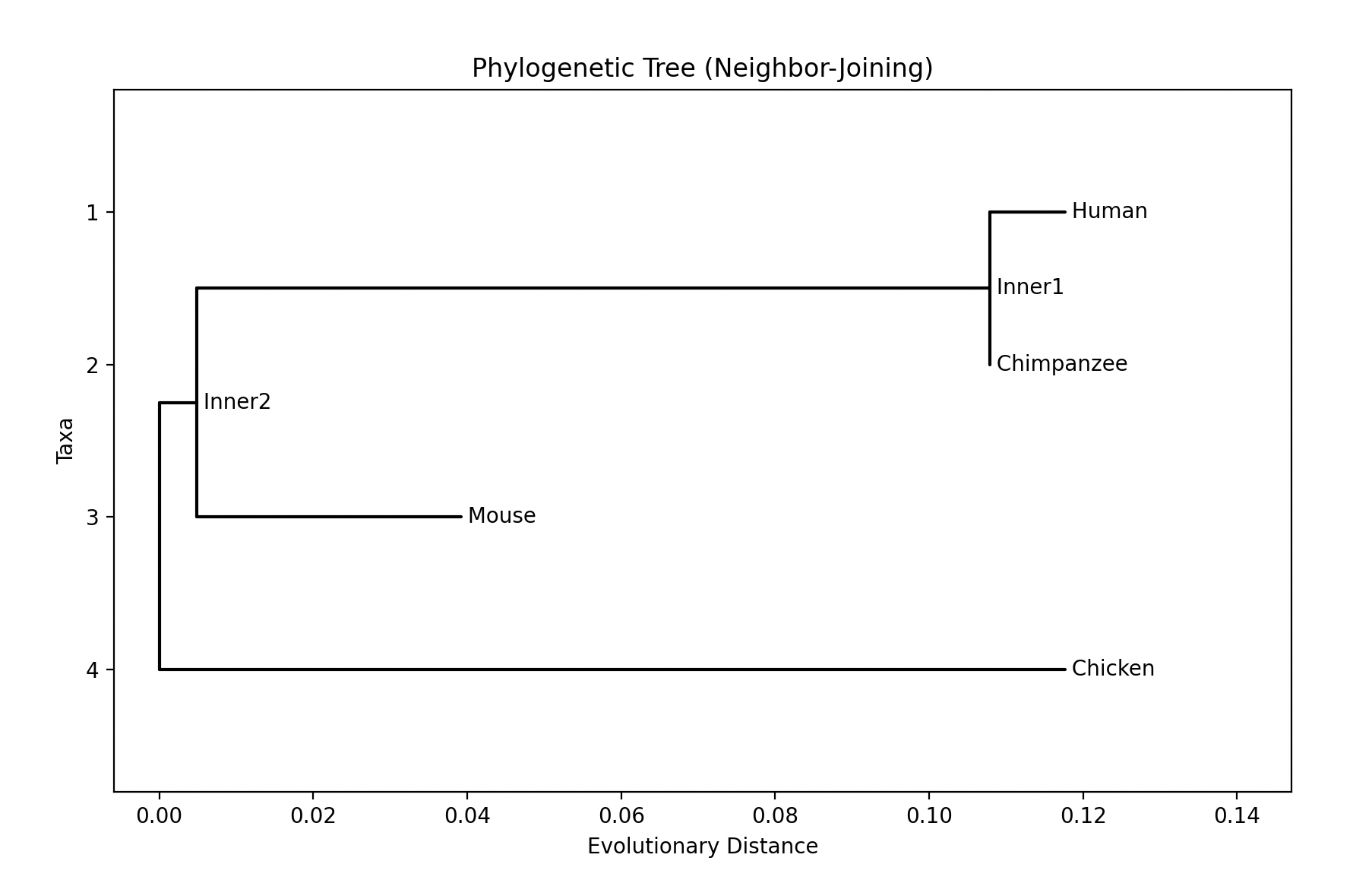
사람과 침팬지가 inner1이라는 가장 가까운 공통 조상에서부터 갈라져 나옴을 알 수 있으며, 두 종으로 뻗어 나가는 branch 길이가 매우 짧은 것을 볼 수 있는데, 이는 두 종의 유전적 차이가 아주 적다는 것을 의미한다.
그 다음으론 쥐, 닭 순서대로 유전적으로 가까움을 알 수 있다.
