Numerical Simulation of Optical Wave Propagation with Examples in MATLAB
https://www.spiedigitallibrary.org/ebooks/PM/Numerical-Simulation-of-Optical-Wave-Propagation-with-Examples-in-MATLAB/eISBN-9780819483270/10.1117/3.866274#_=_

1. 기초 개념

1.1 Convolution

• 원래의 변수(t)가 출력에도 그대로 살아있는 연산의 일종
  $C_{fg}=f(x) \circledast g(x) = \int\limits_{-\infty}^{\infty} f(x')g(x-x')dx'$
  $f(x) \circledast g(x) = \mathcal{F}^{-1}\{\ \mathcal{F}[f(x)] \mathcal{F}[g(x)]\ \}$

두 함수의 차이는, $g(x)$가 conjugate되고 인수의 부호가 반대로 바뀐 것이다.

1.2 Correlation

• 원래의 변수(t)가 다른 변수(τ) 또는 값으로 바뀌어 출력에 나타나는 변환
  $\Gamma_{fg}(\triangle \mathbb{r}) = f(\mathbb{r}) \star g(\mathbb{r}) = \int\limits_{-\infty}^{\infty} f(\mathbb{r})\ g^*(\mathbb{r}-\triangle \mathbb{r})d\mathbb{r}$
  - $\mathcal{F\{g(-t)}\} → G(-f),\ \mathcal{F\{g^*(t)}\} → G^*(-f)$
  - $\mathcal{F\{g^*(-t)}\} → G^*(f)$

• $f(x) \star g(x) = \mathcal{F}^{-1}\{\ \mathcal{F}[f(x)] \mathcal{F}[g(x)]^*\ \}$
  

• 일반적으로, Correlation은 두 신호 사이의 유사성을 결정하는 데 자주 사용.

• 따라서 두 입력 신호 $f(x), g(x)$는 일반적으로 비교적 유사한 특성을 갖는 반면, convolution의 두입력은 보통 서로 매우 다름. 상관관계가 정점에 달하는 seperation $\triangle r$은 두 신호 간의 특징 사이 거리를 알려줄 수 있음.

• 즉, $f(x)=g(x)$인 경우, 자기상관(auto-correlation)

• auto correlation의 peak의 width는 signal의 variation에 대한 정보를 나타낼 수 있다

1.3 optical field와 pupil에 대한 auto-correlation

Auto-correlation 함수
어떤 신호의 시간이동된 자기 자신과의 Correlation 척도

• $u(\mathbf{r})$: optical field
• $w(\mathbf{r})$: window, 광 조리개의 안은 1, 밖은 0

조리개를 통과해 sensor가 모은 data는 다음과 같이 표현가능
$u'(\mathbf{r})=u(\mathbf{r})\ w(\mathbf{r})$

1.3.1 windowed data의 auto correlation

$\Gamma_{u'u'}(\triangle\mathbf{r})=u'(\mathbf{r}) \star u'(\mathbf{r})$

$=\int\limits_{-\infty}^{\infty}u(\mathbf{r})u^*(\mathbf{r}-\triangle\mathbf{r})\ w(\mathbf{r})w^*(\mathbf{r}-\triangle\mathbf{r}) d\mathbf{r}$
위 적분대상함수는 $w(\mathbf{r})w^*(\mathbf{r}-\triangle\mathbf{r})$ 값이 0이 아닌지점에서 단지 $u(\mathbf{r})u^*(\mathbf{r}-\triangle\mathbf{r})$이다.

• 이 영역을 $R(\mathbf{r}, \triangle\mathbf{r})$
• 해당 영역을 계산하면
  - $\Gamma_{ww}(\triangle \mathbf{r})=\int R(\mathbf{r},\triangle \mathbf{r})\ d\mathbf{r}=A(\triangle \mathbf{r})$

$\Gamma_{uu}(\triangle\mathbf{r})$의 평균 값이 $\mathbf{r}$과 독립이고,

$u(\mathbf{r})$이 wide sense stationary(WSS)

• random process $x(t)$의 모든 시간$(-∞ < t < ∞)$에서
  $E[X(t)]$ = $μ_X(t) = μ_X = 일정$
• $x(t)$에서 서로다른 시간에 의한 auto correlation은
  $R_X(t_1,t_2)=R_X(t_1-t_2,0)=R_X(0, t_1-t_2)=R_{XX}(t_1-t_2)$

$\langle \Gamma_{u'u'} (\triangle\mathbf{r})\rangle=\int\limits_{-\infty}^{\infty}\langle u(\mathbf{r}) u^*(\mathbf{r-\triangle r}) \rangle\ \langle w(\mathbf{r})w^*(\mathbf{r}-\triangle\mathbf{r})\rangle\ d\mathbf{r}$
$=\langle u(\mathbf{r}) u^*(\mathbf{r-\triangle r}) \rangle*\langle\int\limits^{\infty}_{-\infty}w(\mathbf{r})w^*(\mathbf{r}-\triangle\mathbf{r}) d\mathbf{r} \rangle$
$=\Gamma_{ww}(\mathbf{\triangle r})\ \langle\Gamma_{uu}(\triangle\mathbf{r}) \rangle$

$=A(\mathbf{\triangle r})\ \langle\Gamma_{uu}(\triangle\mathbf{r}) \rangle$

• Auto-correlation 함수를 Fourier transform하면
  $\Gamma_{u'u'}(\triangle \mathbf{r})=u'(\mathbf{r}) \star u'(\mathbf{r})=\mathcal{F}^{-1}\{\mathcal{F}[u'(\mathbf{r})]\ \mathcal{F}[u'(\mathbf{r})]^* \}$
  - $u'(\mathbf{r}) = \mathcal{F}^{-1}\{U'(\mathbf{f})\}$ 대입
  $=\mathcal{F}^{-1}\{U'(\mathbf{f})\ U'(\mathbf{f})^* \}=\mathcal{F}^{-1}\{|U'(\mathbf{f})|^2 \}$

최종적으로 optical field $u(\mathbf{r})$의 auto-correlation은

$\langle\Gamma_{uu}(\triangle\mathbf{r}) \rangle=\cfrac{\langle \mathcal{F}^{-1} \left\{|U'(\mathbf{f})|^2 \right\}\rangle }{\mathcal{F}^{-1}\left\{|W'(\mathbf{f})|^2 \right\}}$

---

2. Structure function

• 주로 통계학, 물리학, 유체역학, 대기과학 등에서 사용되는 개념

• 일반적으로 두 지점 사이의 변수 차이의 통계적 특성을 설명하는 데 사용

• 구체적으로, 두 지점 간의 거리에 따라 측정된 값의 차이를 분석하여 spatial, temporal scale에 대한 이해를 도움.

• 특히 난류 흐름의 특성을 연구하는데 중요, 난류 내에서의 에너지 variance 같은 현상을 설명

2.1 Structure function

$S_p(r) =\langle |u(x+\mathbf{r})-u(x)|^p \rangle$

• r: 두 지점간의 거리
• $u(\mathbf{r})$: optical field
• $S_p(r)$: 거리 r에 따른 속도 field 또는 기타 물리적 양의 차이의 p차 평균
• $\langle - \rangle$: 앙상블 평균(동일한 물리적 조건을 갖는 시스템의 모든 가능한 상태 또는 표본들의 집합)

2.2 ramdom field $g(\mathbf{r})$의 Structure function 구현

random field $g(\mathbf{r})$은 다음으로 정의

$D_g(\triangle \mathbf{r}) = \int[g(\mathbf{r})-g(\mathbf{r-\triangle r})]^2 d\mathbf{r}$
$=\int[g(\mathbf{r})^2+g(\mathbf{r}-\triangle\mathbf{r})^2-2g(\mathbf{r})\ g(\mathbf{r}-\triangle \mathbf{r})] d\mathbf{r}$

random field $g(\mathbf{r})$이 통계적으로 등방성일 때, 어떤 방향에서도 동일한 확률 분포를 갖는다는 뜻.
$g(\mathbf{r})$과 $g(\mathbf{r}-\triangle\mathbf{r})$ 는 분포 자체는 동일하므로 $\int$ 값이 동일

mean structure function과 auto-correlation간의 관계는 다음과 같다.

• $\Gamma_{gg}(0)=\int\limits^{\infty}_{-\infty}g(\mathbf{r})g^*(\mathbf{r})d\mathbf{r}=\int\limits_{-\infty}^{\infty}g(\mathbf{r})^2d\mathbf{r}$
• $\Gamma_{gg}(\triangle\mathbf{r})=\int\limits^{\infty}_{-\infty}g(\mathbf{r})g^*(\mathbf{r}-\triangle\mathbf{r})d\mathbf{r}$
• $D_g(\triangle\mathbf{r})=2[\Gamma_{gg}(0)-\Gamma_{gg}(\triangle\mathbf{r})]$

$D_{u'}(\triangle\mathbf{r})=\int[u'(\mathbf{r})-u'(r-\triangle\mathbf{r})]^2\ d\mathbf{r}$
$=\int[u'(\mathbf{r})^2\ w(\mathbf{r}-\triangle\mathbf{r})-2u'(\mathbf{r})u'(\mathbf{r-\triangle r)}+u'(\mathbf{r-\triangle r})^2\ w(\mathbf{r})]\ d\mathbf{r}$

• $w(r)=\cfrac{1}{2\pi}\int\limits^{\infty}_{-\infty}W(\mathbf{f})\ e^{jwt}$

• $u'(r)=\cfrac{1}{2\pi}\int\limits^{\infty}_{-\infty}U'(\mathbf{f})\ e^{jwt}$
• $[u'(r)]^2=\cfrac{1}{2\pi}\int\limits^{\infty}_{-\infty}S(\mathbf{f})\ e^{jwt}$
• $w(\mathbf{r})$은 실수, $W(\mathbf{f})=W^*(\mathbf{f})$

$D_{u'}(\triangle\mathbf{r})=\int\int\limits_{-\infty}^{\infty}\int\limits_{-\infty}^{\infty}\{S(\mathbf{f_1})W^*(\mathbf{f_2})+S^*(\mathbf{f_2})W(\mathbf{f_1})-2U'(\mathbf{f_1})[U'(\mathbf{f_2})]^* \times e^{j2\pi(\mathbf{f_1}+\mathbf{f_2})\cdot \mathbf{r}}e^{j2\pi\mathbf{f}_2\triangle\mathbf{r}} d\mathbf{f_1}\ d\mathbf{f_2}\ d\mathbf{r} \}$

$\mathbf{r}$에 대해 적분 후, $\mathbf{f}_2$에 대해 적분하면

$D_{u'}(\triangle \mathbf{r})=\int\limits_{-\infty}^{\infty}\{S(\mathbf{f_1})W^*(\mathbf{f_1})+S^*(\mathbf{f_1})W(\mathbf{f_1})-2U'(\mathbf{f_1})[U'(\mathbf{f_1})]^*]\}\ e^{\ j2\pi\mathbf{f_1}\cdot\triangle\mathbf{r}}d\mathbf{r_1}$

$=2*\int\limits^{\infty}_{-\infty}\{Re[S(\mathbf{f_1})W^*(\mathbf{f_1})]-|U'(\mathbf{f_1})|^2\}e^{j\ 2\pi\mathbf{f_1}\cdot\triangle\mathbf{r}}\ d\mathbf{f_1}$
$=2\ \mathcal{F}^{-1}\{Re[S(\mathbf{f_1})W^*(\mathbf{f_1})]-|U'(\mathbf{f_1})|^2\}$

---

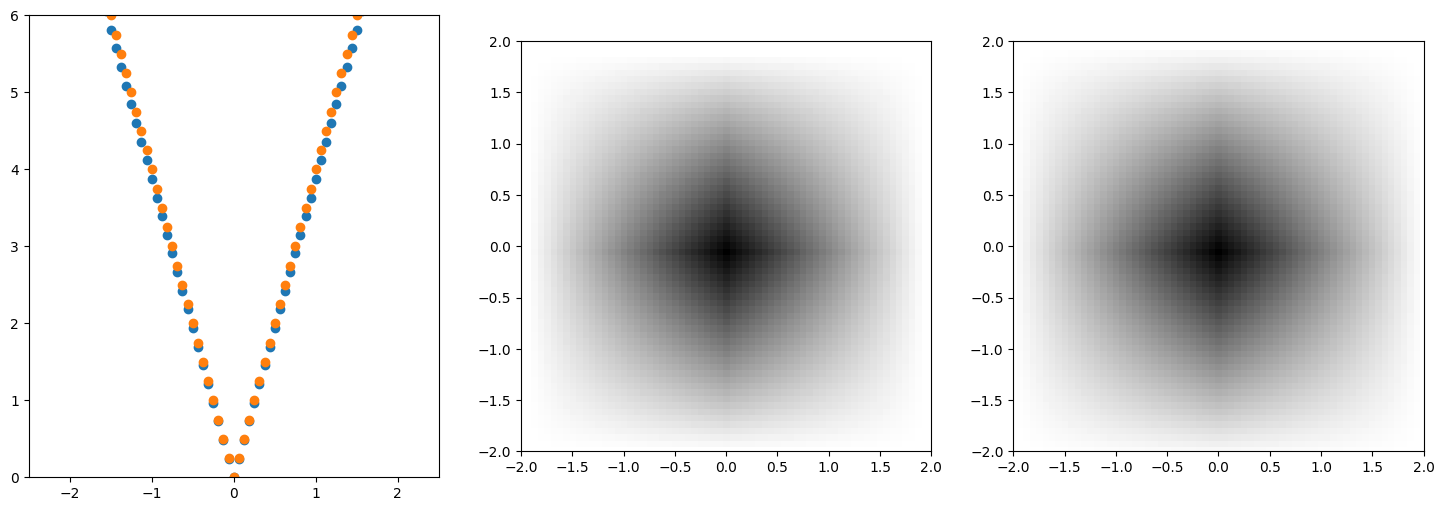
3. structure function of the 2D signal 계산

$A (x, y) = rect (x/w)\ rect (y/w)$.

import numpy as np
import matplotlib.pyplot as plt

N = 256     # number of samples
L = 16      # grid size [m]
delta = L/N # sample spacing [m]
F = 1/L     # frequency-domain grid spacing [1/m]
x= np.arange(-N/2, N/2)*delta

freqs = np.fft.fftfreq(N*N, d=delta).reshape(N,N)
[x, y] = np.meshgrid(x, x)
w = 2

A = rect2(x,w) * rect2(y,w)
mask = np.ones((N,N))

# perform digital structure function
C = str_fcn2_ft(A, mask, delta) /delta**2
C = np.fft.fftshift(C) 
# continuous structure function
C_cont = 2 * w**2 * (1-tri(x,w)*tri(y,w))

plt.figure(figsize=(18,6))
plt.subplot(1,3,1)
plt.xlim(-2.5,2.5)
plt.ylim(0,6)
plt.scatter(np.arange(-N/2,N/2)*delta,np.real(C[128]))
plt.scatter(np.arange(-N/2,N/2)*delta,np.real(C_cont[128]))

plt.subplot(1,3,2)
plt.imshow(np.real(C), cmap='gray', extent=(x.min(), x.max(), x.min(), x.max()))
plt.xlim(-2,2)
plt.ylim(-2,2)
plt.subplot(1,3,3)

plt.imshow(C_cont,cmap='gray', extent=(x.min(), x.max(), x.min(), x.max()))
plt.xlim(-2,2)
plt.ylim(-2,2)
plt.show()