Optical Wave Propagation 수치 시뮬레이션

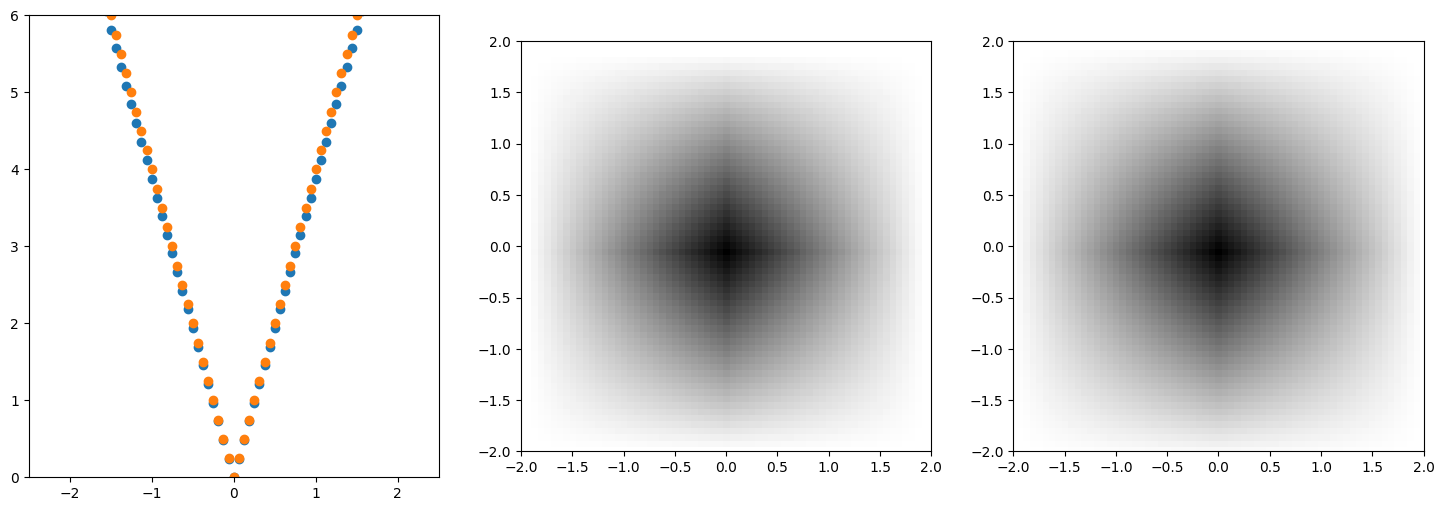
1. 기초 개념 1.1 Convolution 원래의 변수(t)가 출력에도 그대로 살아있는 연산의 일종 $C{fg}=f(x) \circledast g(x) = \int\limits{-\infty}^{\infty} f(x')g(x-x')dx'$ $f(x) \circleda

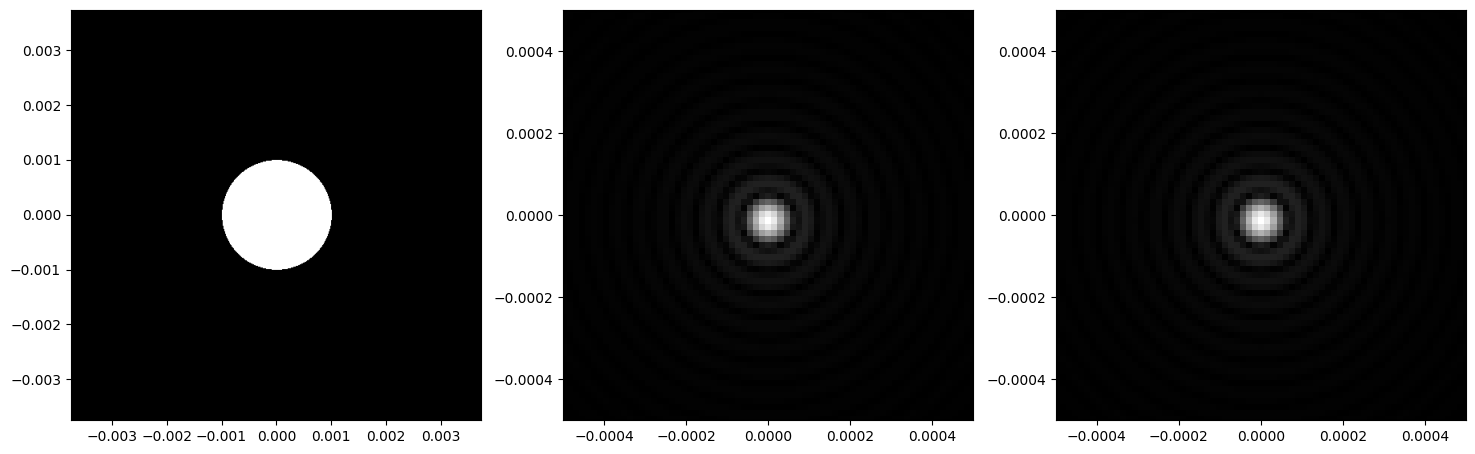
정확한 결과를 얻기 위해, Fresnel 회절 적분을 수치적으로 평가하는 것이 필요. 먼저 Fraunhofer 근사와 렌즈를 사용한 회절 2가지를 다뤄보자. 0. Scalar 회절 이론 대부분의 경우, 광학 소스는 단순한 평면, 구형 또는 가우시안 광선 파동이 아님

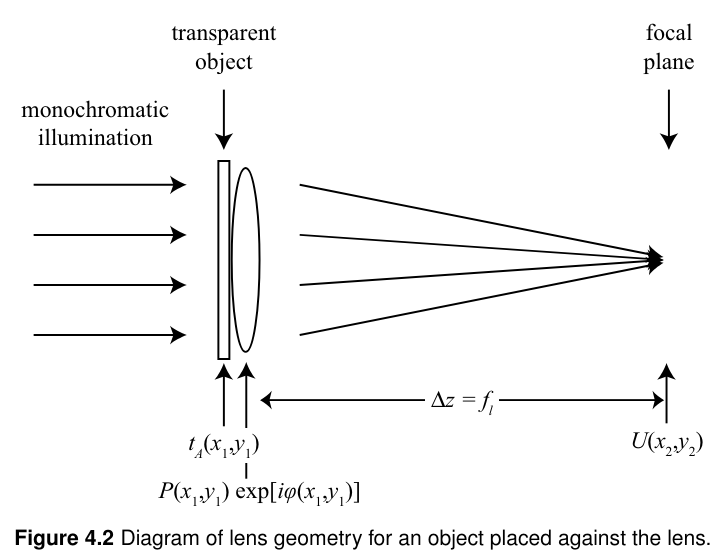
이번에는 near-field diffraction(근거리 회절)애 대해 다루고자 한다.이는 단색(monochromatic) 파동에 대한 paraixal approximation(축 근사)를 사용하는 Fresnel 회절 적분에 의해 결정된다.$U(x2,y_2)=\\cfr

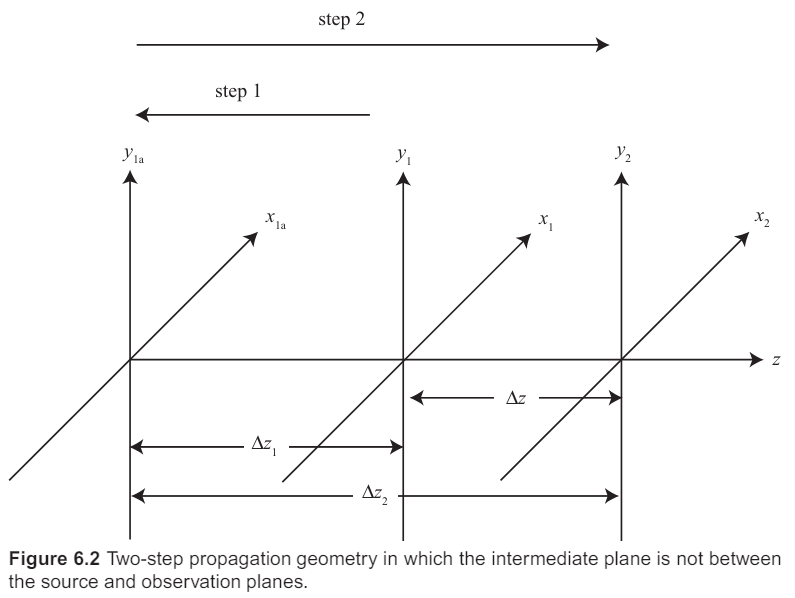
여기서는 near-field(근거리) optical wave 전파에 대해 높은 정확도와 유연함을 가지고 모델링하는 기법을 소개한다. 원거리 전파보다는 상당히 더 어렵다. Fresnel 회절 적분과 다른 형태로 다른 방법으로 수치적으로 계산되며 각 장점과 단점을 논의한

Fresnel 회절 적분은 convolution form 형태로 평가되는데 $U(x2,y2)=U(x1,y1)\ \circ[\cfrac{e^{ik\triangle z}}{i\lambda \triangle z}\ e^{i\frac{k}{2\triangle z}(x1^2+

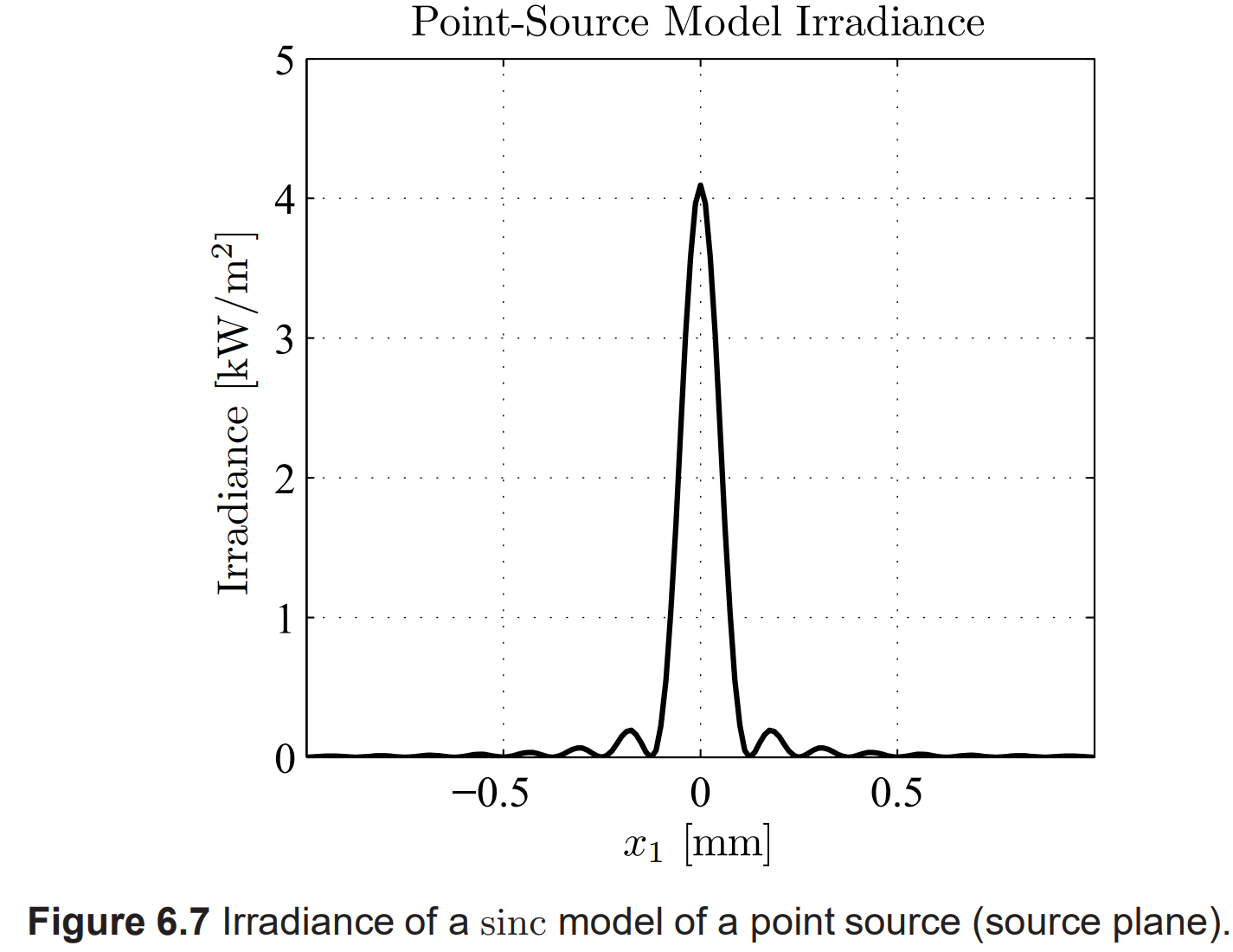
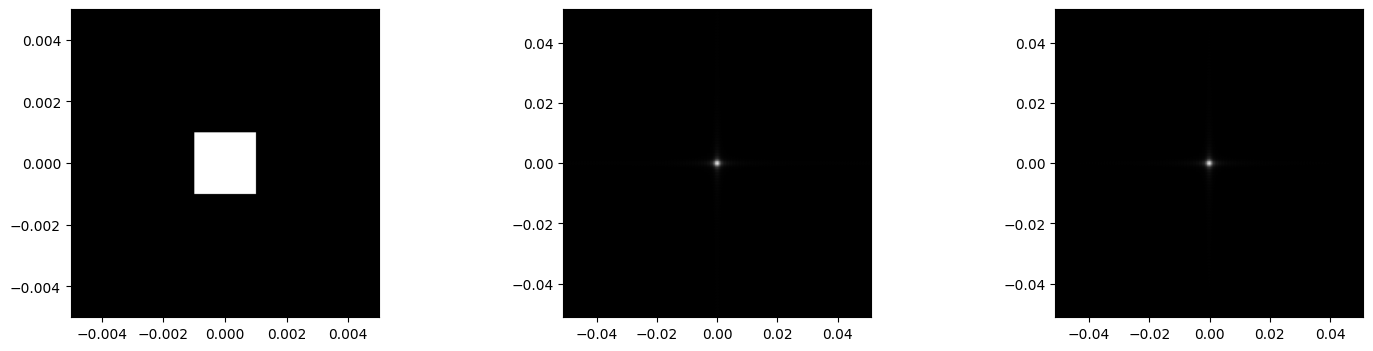
point source를 모델링하기에는 어렵다. 실제 point source $U{pt}(\mathbf{r1})$는 dirac delta 함수에 의해 표현되는데, 이때 $x1, y1$ 평면에서 point source 위치는 $\mathbf{r}c=(xc,y_c)$이

simulation은 분석적으로 다루기 어렵지만, 어떤 컴퓨터 code로 어떤 source field여도 optical-wave 전파를 시뮬레이션할 수 있다. Wave-optics 시뮬레이션은 DFT들에 기반하므로, aliasing은 DFTs에 어려움을 준다. wav

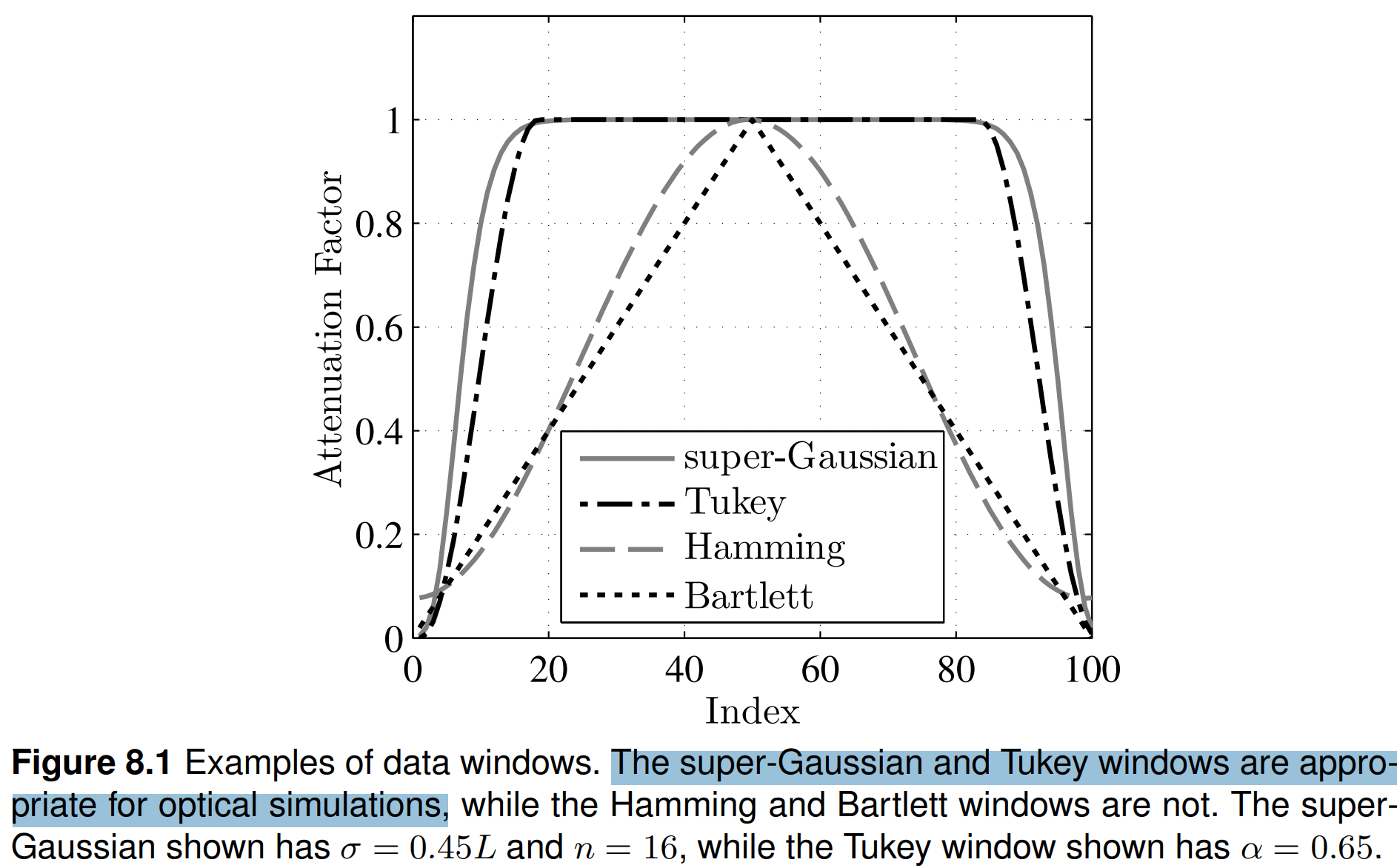
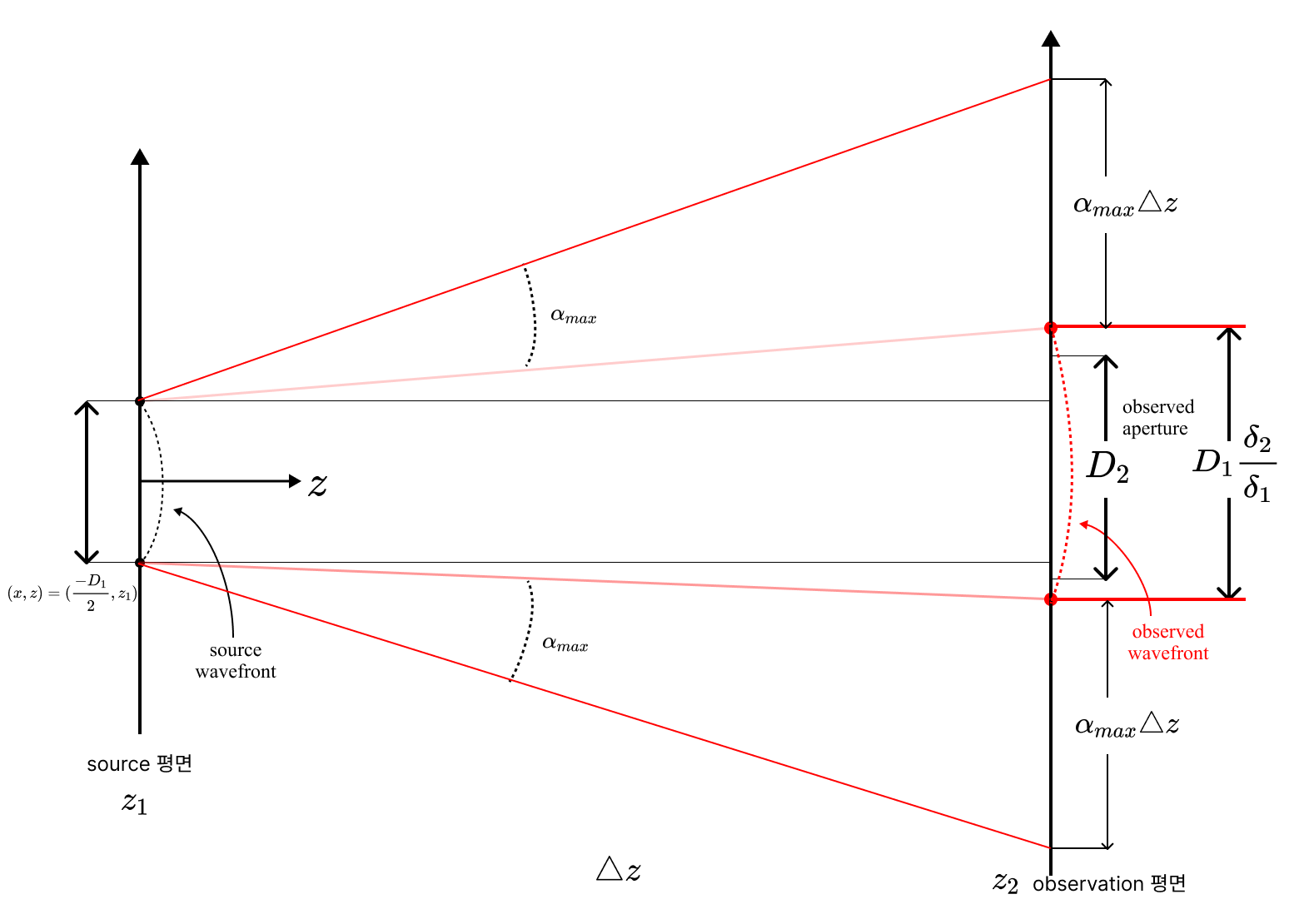
Fresnel propagation의 sampling 제약 조건은 엄격하다. 특히, angular-spectrum 방법은 짧은 거리 전파에 가장 적합하다. 주요 문제는 aliasing으로 인해 발생하는 wrap-around이다. 이러한 효과를 완화하기 위해 몇 가지 접

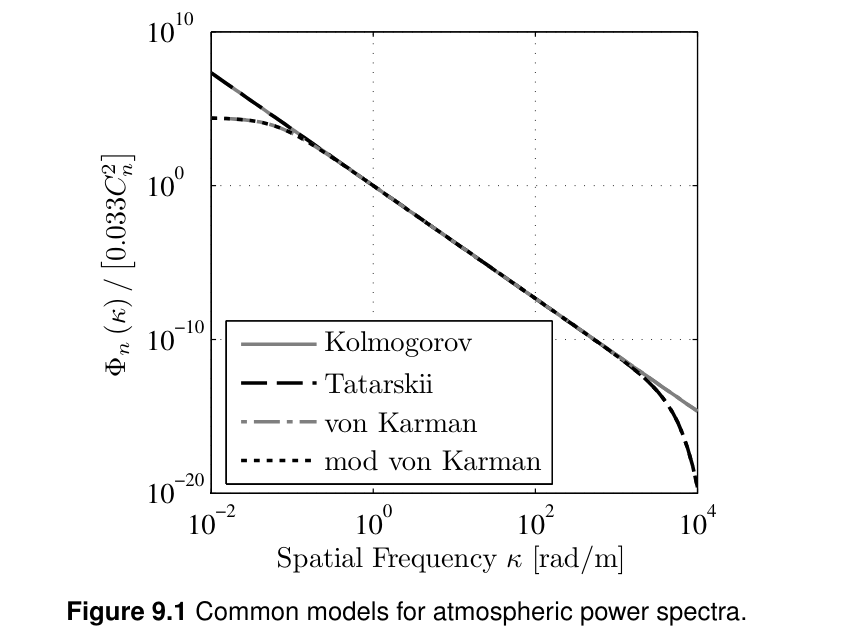
Kolmogrov에 의해 turbulent flow의 original 분석을 시작하는데 결국 굴절률 분산의 통계적 모델을 이끈다. pertrubation 이론은 observation 평면 optical field의 유용한 통계 특성을 얻기 위해 Maxwell 방정식을

광 전파에서 대기 turbulence 효과를 분석적 결과로 도출하는 것은 간단한 통계적 모델을 가정할 때 가능하다. 하지만, 적응 광학 시스템을 사용하여 더 복잡한 시나리오를 고려하는 것을 원하는 경우, 보통 보정된 optical field의 통계는 closed for

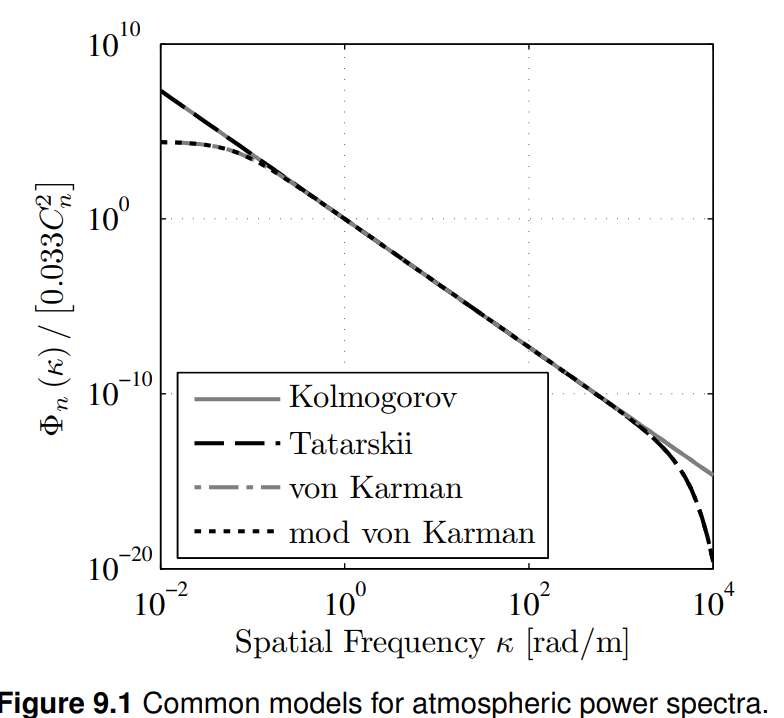
대기의 굴절률 변동은 random process이며, 이를 통과하는 광 경로 길이도 마찬가지로 무작위적입니다. 결과적으로 turbulence model들은 통계적 평균(structure function, 굴절률 변동의 power spectrum)을 준다. atmosph

아래 예제 simulation은 point source가 $Cn^2=1\times10^{-16}m^{-2/3}$인 거리 $\triangle z=50km$를 turbulent path를 통과하는 것이다. 단순함을 위해, Kolmogorv refractive-index P