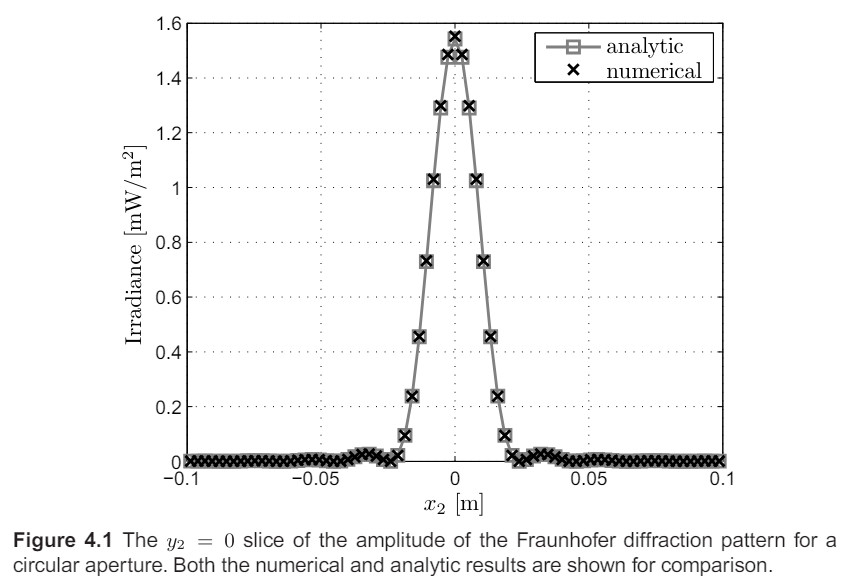
정확한 결과를 얻기 위해, Fresnel 회절 적분을 수치적으로 평가하는 것이 필요.
0. Scalar 회절 이론
스칼라 회절 이론(scalar diffraction theory)은 전자기파의 벡터 성질을 무시하고 파동은 스칼라 량으로 근사화하여 회절 현상을 설명하는 이론
- 매질은 선형, 등방성, 비분산성
- 파장이 작은 가시광선 영역에서는 유효한 근사
- 회절은 호이겐스 원리와 프레넬 적분 등을 이용하여 계산
- 빛의 진행 경로를 무한 개의 2차 파원의 중첩으로 표현
- 단일 구멍이나 간단한 개구에 대한 회절 패턴 해석에 주로 사용
- 전자기 이론에 비해 수학적으로 단순하여 해석과 계산이 용이합니다.
회절 현상의 벡터 특성, 편광 효과 등은 전자기 이론으로 설명해야함.
대부분의 경우, 광학 소스는 단순한 평면, 구형 또는 가우시안 광선 파동이 아님.
source plane에서 과 observation plane에서 이고 사이 거리를 라고 할 때
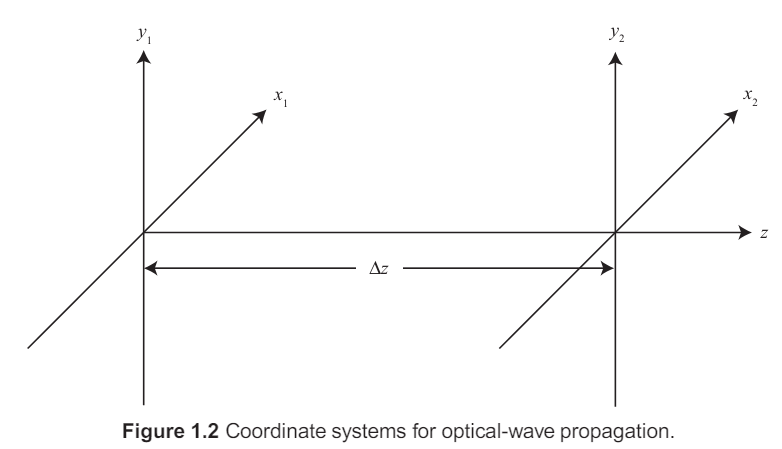
문제: source-plane에서 을 source plane에서 optical field일 때, 을 observation plane에서 optical field는 무엇인가?
solution은 Fresnel 회절 적분으로 주어짐.
paraxial approximation이란?
- 빛이 주로 한 축으로 진행한다고 가정하는 근사적인 방법
- 빛이 근축(paraxial) 근처에서 작은 각도로만 퍼져 나가는 것으로 가정하는 것
위 식의 해석적인 solution은 손에 꼽을 정도 밖에 없다. 즉 Fresnel 회절 문제들 중 해석적인 답을 얻을 수 있는게 몇 안되고 사각 구경 등이 있다.
정확한 결과로 Fresnel 회절 적분을 수치적으로 평가하는 것은 몇 가지 흥미로운 도전이다. 이 도전은 컴퓨터에서 유한 크기의 grid에서 discrete한 샘플을 사용해야해서 발생한다.
스칼라 회절 이론에서 푸리에 변환이 너무 자주 발생하기 때문에 이에 집중.
위 방정식은 푸리에 변환의 형태로 쓸수 있으며, DFT를 효율적으로 계산할 수 있기 때문에 바람직한 식이다.
- Ch2. 이산 푸리에 변환
- Ch3. 푸리에 변환의 기본 계산
- CH4. Free space을 통해 매우 멀리 전파된 상황 및 렌즈가 있는 상황
- 전파거리가 매우 먼 경우에는 를 만족을 하면 위 방정식 이차 위상 요소를 평평한 것으로 근사화 가능. D는 source-plane에서 최대 공간 범위.- 이것은 Fraunhofer 근사 -> Fraunhofer 회절 적분
1. Fraunhofer 회절
빛이 source 구경()으로부터 전파될 때, observation 평면()에서 optical field가 Fraunhofer diffraction integral에 의해 근사될 수 있다.
Goodman에 따르면 매우 먼 정의는
전파 거리()가 파장에 대한 source 구경의 지름의 제곱 비보다 크면 된다.
이것은 source를 위에서 거의 평평한 2차(quadratic) 위상을 갖기 때문에 좋은 근사이다.
Fraunhofer 적분은 Fourier Transform 형태로 변환할 수 있다.
| 기호 | 의미 |
|---|---|
| source-plane 좌표 | |
| observation-plane 좌표 | |
| grid spacing in source-plane | |
| grid spacing in observation-plane | |
| source와 observation plane 사이 거리 |
grid의 특성을 위에 표같이 정의한다.
source plane에서 spatial frequency 변수는
이고, grid spacing은
이 공간 주파수가 observation plane 에 직접 매핑된다.
수치적으로 Fraunhofer diffraction 적분을 계산하면 적절한 곱샘과 spatial scailing으로 Fourier Transform을 수행한다.
위에 는 무시된다. 그것은 단지 진행방향 축 상에서 위상이기 때문이다.
1.1 예제
원형 구경에서 먼 거리의 observation 평면까지 단색 평면파의 전파를 시뮬레이션한다.
큰 영역을 보여주면, 가장자리에 일부 불일치가 나타난다. 이는 aliasing 때문. 예제 코드가 만약에 0.4m 지름인 시스템을 모델링한 경우, aliasing이 수치 예측과 실험적으로 측정된 회절 패턴 간의 비교에 크게 영향을 미치지 않는다.
선택된 grid spacing과 grid point 수는 이 목적에 충분하다.
좀 더 구체적으로 설명하면, 전파의 기하학적 구조가 소스의 관측가능한 공간 주파수 콘텐츠에 한계를 부과한다. observation-plane 좌표는 다음과 같이 source의 spatial frequency와 관련있다.
만약에 plane에서 센서 너비가 0.4m면,
observation-plane에서 가질 수 있는 최대 좌표 값은
이것은 source에서 관측 가능한 최대 공간 주파수 값으로 이어진다.
결과적으로, 이 시뮬레이션에서 실제 source의 대역 제한하여(filtered) 전파시키면, 실험실에서 관찰할 수 있는 것과 동일한 observation-plane에 회절 패턴을 생성할 것이다.
함수 정의
import numpy as np
import matplotlib.pyplot as plt
from scipy.special import j1
def rect2(t,T):
return np.where(np.abs(t) < T/2, 1, 0)
def fraunhofer_prop(Uin, wavelength, delta_l, distance):
k = 2*np.pi/wavelength # optical wavevector
fX = np.arange(-N/2, N/2) / (N*delta_l)
# observation-plane 좌표
ob_coor = wavelength*distance*fX
[x2, y2] = np.meshgrid(ob_coor, ob_coor)
# evaluate the Fresnel-Kirchhoff integral but with
# the quadratic phase factor inside cancelled by the phase of the lens
Uout = np.exp(1j*k/(2*distance)*(x2**2+y2**2)) / (1j*wavelength*distance) * np.fft.fft2(Uin) * (delta_l**2)
return Uout, x2, y2
def jinc(x):
for i, row in enumerate(x):
for j, col in enumerate(row):
if col == 0.0:
x[i,j] = 0.5
else:
#print(x[i,j])
x[i,j] = j1(2*np.pi*x[i,j])/(2*np.pi*x[i,j])
return x
def circ(x, y, D):
return np.where((x*x+y*y)<D**2, 1, 0)위 식의 FT 이용 계산과 기존 적분 결과 비교
N = 512 # number of grid points per side
L = 7.5e-3 # total size of the grid [m]
delta_l = L/N # source-plane grid spacing [m]
D = 1e-3 # diameter of the aperture [m] 1mm
wavelength = 1e-6 # 1000nm
k = 2*np.pi/wavelength
distance = 20 # propagation distance [m]
x = np.arange(-N/2, N/2)*delta_l
[x1, y1] = np.meshgrid(x,x)
Uin = circ(x1, y1, D)
Uout, x2, y2 = fraunhofer_prop(Uin, wavelength, delta_l, distance)
Uout_shift = np.fft.fftshift(Uout)
# analytic result
Uout_th = np.exp(1j*k/(2*distance)*(x2**2+y2**2)) / (1j*wavelength*distance) * D**2 * np.pi/4 * jinc(D*np.sqrt(x2**2+y2**2)/(wavelength*distance))2D 회절 시각화
plt.figure(figsize=(18,6))
plt.subplot(1,3,1)
plt.imshow(np.real(Uin), cmap='gray', extent=(x1.min(), x1.max(), y1.min(), y1.max()))
plt.subplot(1,3,2)
plt.imshow(np.abs(Uout_shift),cmap='gray', extent=(x1.min(), x1.max(), y1.min(), y1.max()))
plt.xlim(-0.0005,0.0005)
plt.ylim(-0.0005,0.0005)
plt.subplot(1,3,3)
plt.imshow(np.abs(Uout_th),cmap='gray', extent=(x1.min(), x1.max(), y1.min(), y1.max()))
plt.xlim(-0.0005,0.0005)
plt.ylim(-0.0005,0.0005)
plt.show()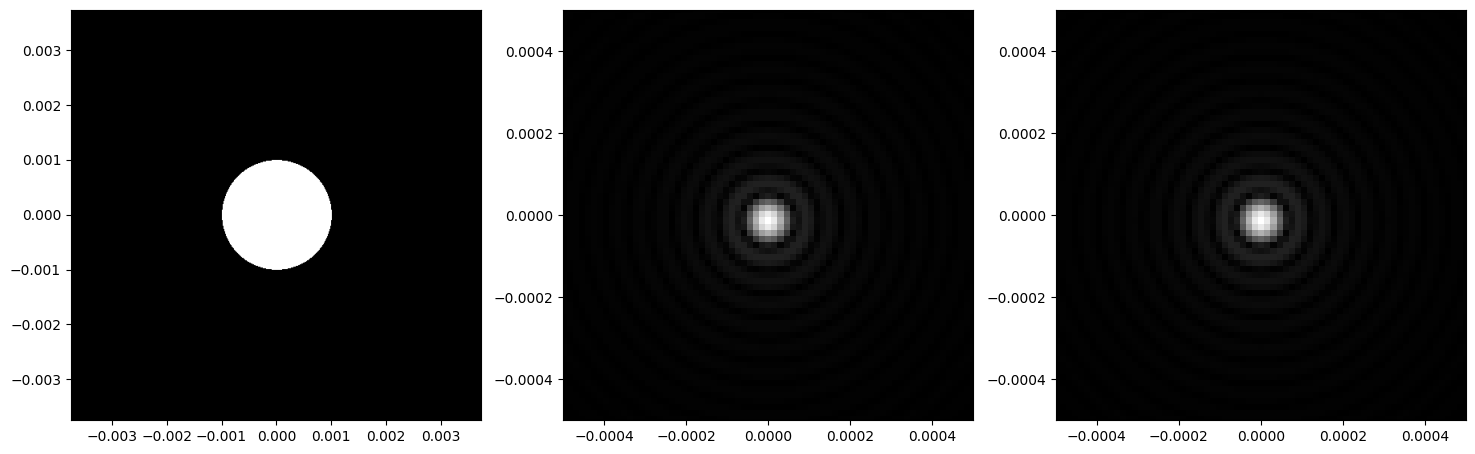
1D 시각화
plt.figure(figsize=(18,6))
plt.subplot(1,3,1)
plt.xlim(-0.1, 0.1)
plt.ylim(0, 0.16)
plt.plot(x2[1], np.abs(Uout_shift[int(N/2)]), marker='x')
plt.plot(x2[1], np.abs(Uout_th[int(N/2)]), marker='s')
plt.show()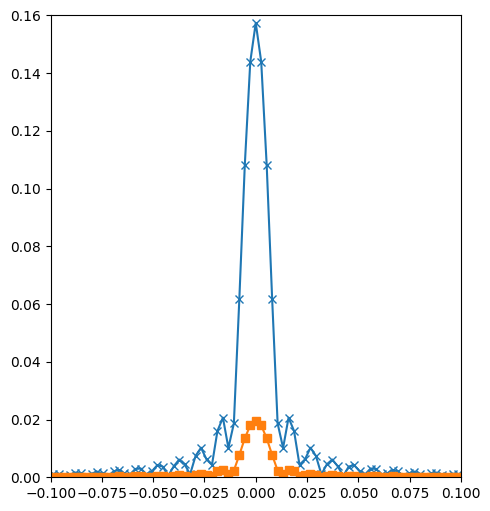
원래 나와야 하는 결과