PID 제어기는 feedback 제어기의 형태를 가지고 있음.
제어 대상에 의해 정해지는 입력(Input)을 측정하여 이를 목표로 하는 설정 값(setpoint)와 비교하여 오차(error)를 계산.
$Error = Setpoint - Input$

이 오차 값을 이용하여 제어에 필요한 제어 값(Output)을 계산.
이 제어 값은 다시 제어하고자 하는 대상의 Input으로 사용되는 구조

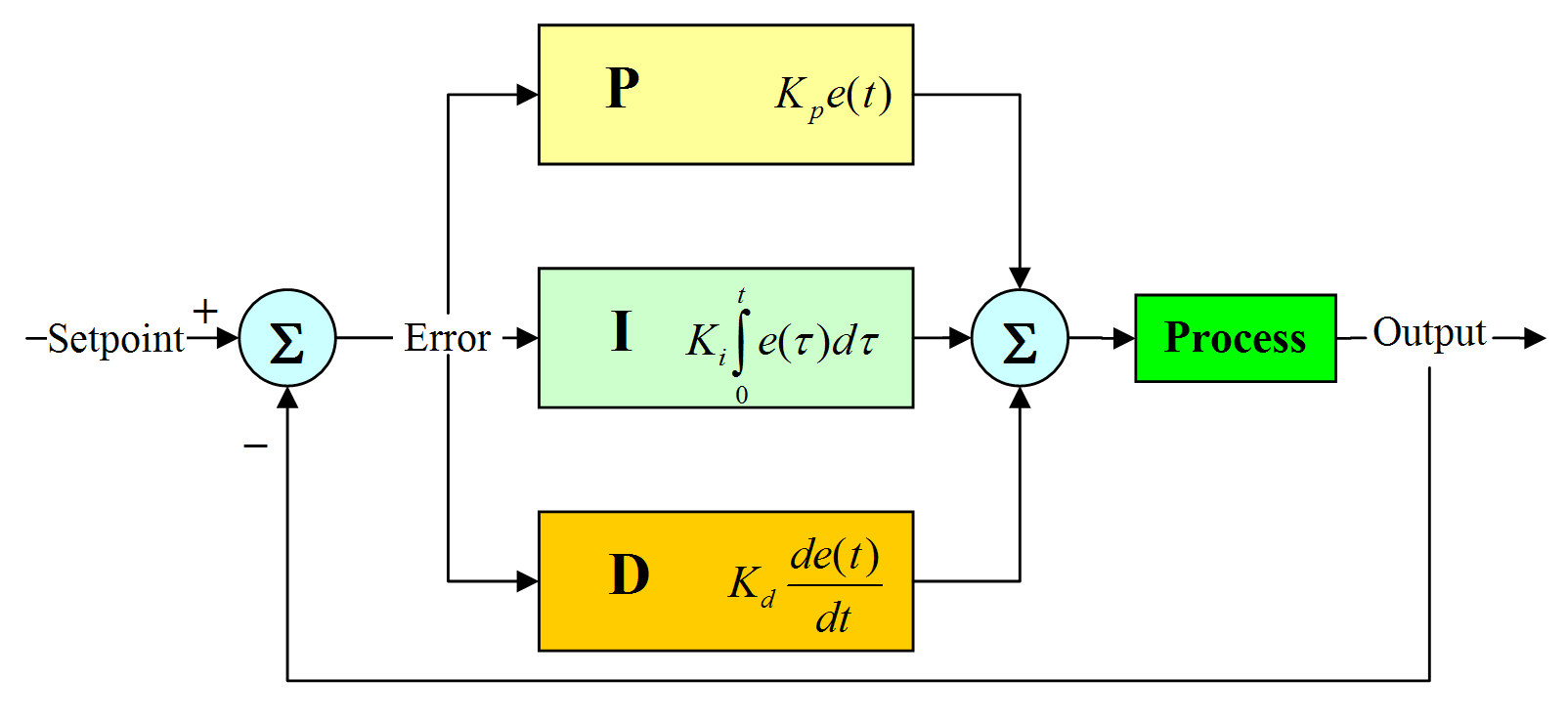
1. 표준적인 PID 제어기

MV : Maniputlated Variable(제어 값)

$MV(t) = K_p*e(t)+K_2*\int^t_0 e(r)dr+K_d*\frac{de}{dt}$

1. $K_p*e(t)$ : 비례 항. 현재 상태에서의 오차 값 크기에 비례한 제어.
2. $K_2*\int^t_0e(r)dr$ : 적분 항. 일정한 상태로 유지되서 발생하는 오차를 없애기.
3. $K_d*\frac{de}{dt}$: 미분 항. 출력 값의 급격한 변화로 인한 오차가 안생기도록 반대로 제동을 걸어 목표 값을 지나가 버리는 overshoot을 줄여 stability 향상.

1.1 Crazyfile Drone

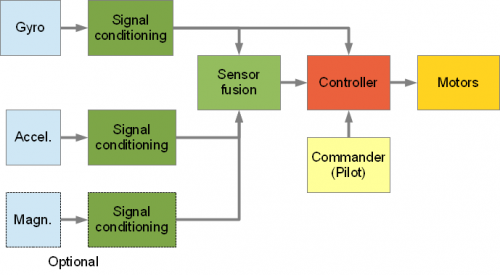
다음 3가지가 Controller에 들어가서 모터가 제어된다.

• 자이로센서, 가속도계, 지자기 센서 값이 Sensor Fusion된 값
• Pilot이 조종한 Commander
• 자이로센서 값
  

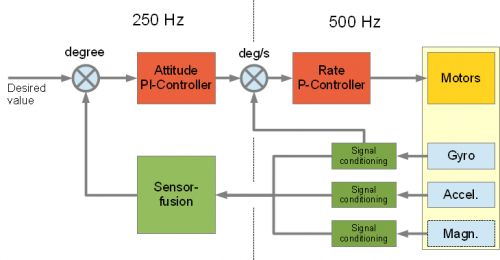
PID 제어기는 250Hz로 각도를 구하고, 500Hz로 각속도를 구함.

• 가속도, 자이로 센서를 이용해 구한 각도($\theta$)에 대해서 PI 연산을 수행
• 자이로 센서를 이용해 구한 각속도($\omega$)에 대해서 P 연산을 수행해 더한 후, 모터 제어
  

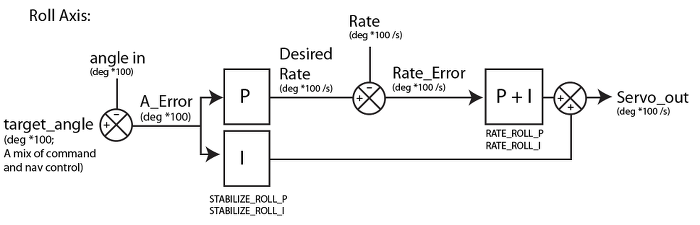
1.2 ArduPilot Drone

이중 PID 제어기가 쓰임

Roll 제어를 위한 이중 PID 제어기

1. $\theta_{Error}=\theta_{target}-\theta_{in}$ 가속도 센서를 통해 얻은 각도($\theta_{in}$) 오차 값에 비례한 값은 P, 누적시킨 값은 I.
2. P 값의 오차($\theta_{Error}$)는 움직여야 되는 $\omega_{desired}$라고 생각
3. 자이로센서를 통해 얻은 $\omega$는 $\omega_{error}=\omega_{desired}-\omega$ 각속도 오차에 대해 P, I값을 구하고
4. 둘을 더해 서보 모터로 나가는 출력을 계산
   

1.3 P term

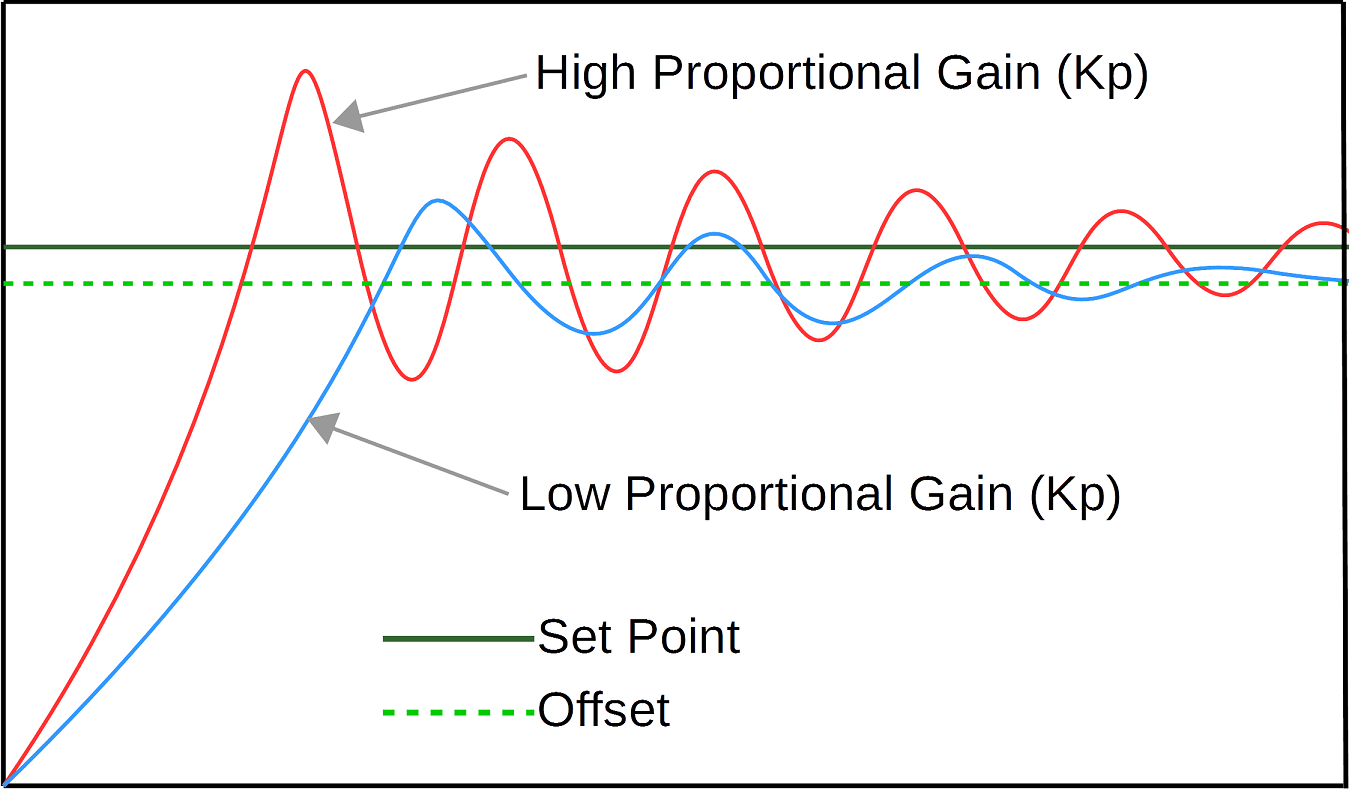
error에 따라 output을 바꾼다.
$K_p$ 를 변경함에 따라 제어기는 변화에 크게 또는 작게 반응할 수 있음

$P_{out}=K_p*e$
$K_p$ 값이 크면 제어기는 더 빨리 Setpoint에 도달하지만, 시스템은 Setpoint 근처에서 진동하며 불안정한 상태.
$K_p$ 값이 작으며 제어기는 더 늦게 Setpoint에 도달하지마, 몇 번 진동후 setpoint 아래에서 일정한 오차를 가지며 안정한 상태.
오차에 가까울수록 Output이 작기 때문에,
시스템이 Setpoint에 닿는데 필요한 충분한 힘을 Output에 공급하지 못함.

1.4 I term

현재 오차뿐마 아니라, 누적 오차에 따라 출력을 보고 바꿀 수 있어야 함. 적분 항은 시간에 걸친 오차의 합. 오차가 클 경우 적분 항에 의해 시간이 지나면서 오차의 합이 쌓이며 출력은 빠르게 변해 오차를 제거.

$P_{out}=K_p*e+K_i*\int e$

P term에서 낮은 $K_p$의 응답곡선에 적분 항을 더해 얻은 PI 응답 곡선
$K_i$ 값이 크며 시스템은 더 빨리 Setpoint에 도달함. 파형의 상승부가 크지마 불안정한 상태로 남지 앟음.
$K_i$가 중간 값이며 더 늦게 Setpoint에 도착하지만, 시스템이 적은 진동으로 훨씬 빠르게 안정.
$K_i$가 최적 값이며 아주 늦게 Setpoint에 도착하지만, 거의 진동 없이 Setpoint에 도착해 안정.

1.5 D term

미분항으로써, 오차 변화율을 계산하고 그 결과를 출력에 더함.
만약 오차의 변화가 크지 않다면 미분 항의 값은 작으며 출력에 영향을 크게 미치지 않음. 그러나 오차가 갑작스레 크게 변하면 시스템의 진동을 피하기 위해 미분 항의 값은 커짐.
$D=K_d*(e_n-e_{n-1})$

PID 제어기 출력: $P_{out}=K_p*e+K_i*\int e + K_d*(e_n-e_{n-1})$

1.6 PID 튜닝 방법

PID 제어기에서 결정해야 하는 매개변수 $K_p, K_i, K_d$ 이다.
이는 증폭 값 혹은 Gain이라고 하며, 수학적, 실험적-경험적 방법을 통해 계산하는 것을 튜닝

Ziegler-Nichols

경험적으로 PID 제어기를 조절하는 방법

Control Type	$K_p$	$K_i$	$K_d$
P	$0.5*K_u$	-	-
PI	$0.45*K_u$	$1.2*\frac{K_p}{T_u}$	-
PID	$0.6*K_u$	$2*\frac{K_p}{T_u}$	$K_p*T_u/8$

적절한 $K_u$, $T_u$를 어떻게 구할까?

1. $K_i$, $K_d$ 증폭 값을 0으로 설정하고, $K_p$ 값을 0부터 시작해서 시스템 출력 값이 일정한 진폭으로 진동할 때까지 증가시킴.
   • $K_u$(최대 Gain 값): 시스템의 출력 값이 일정한 진폭으로 진동하는 시점의 $K_p$ 값
   • $T_u$: 이 시점의 진동 주기
2. 이렇게 $K_u$, $T_u$ 값을 구했다면, 사용되는 제어기의 형태에 따라 $K_p$, $K_i$, $K_d$ Gain 값을 설정 가능

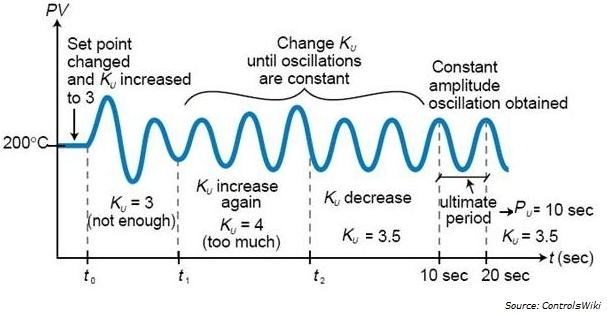
1. $K_u=3$: 시스템의 출력 값이 수렴하는 구간. 원하는 값 X
2. $K_u=4$로 증가: 시스템 출력이 점차 발산함. 원하는 값 X
3. $K_u=3.5$로 감소: 시스템 출력이 일정하게 진동. 우리가 원하는 $K_u$, $T_u$

드론 Gain 조절

---

2. PID 제어기 알고리즘

Error = Setpoint - Input
PTerm = Kp * Error
ITerm += Ki * Error * dt

적분항은 Ki에서 현재 오차와 센서입력 주기 값을 곱해 더해줌. 미세값 반복으로 더하기

dError = Error - prevError
DTerm = Kd * (dError / dt)

미분항(DTerm)을 구하기 위해서는 오차의 변화율이 필요.
오차 변화(dError)는 현재 오차(Error)에서 이전 오차(prevError)를 뺀 값에 센서 입력 주기 값을 나눔.

Output = PTerm + ITerm + DTerm

미분항의 경우 실제로는

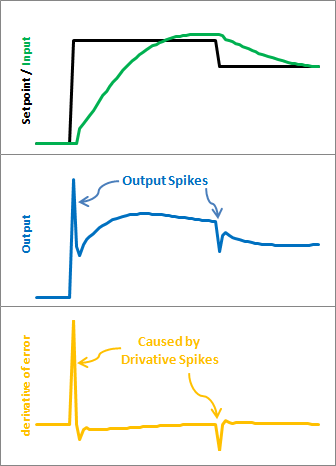
1. 검은 선은 Setpoint. 두번 Setpoint 값을 변경했다. 예를 들어, 드론을 이동하기 위해 사용자가 Roll 값을 변경하는 상황.
2. Output 값(드론 모터속도)이 급격하게 변하는 부분이 발생하는 것을 볼 수 있다. 이것은 드론의 모터 속도를 갑자기 높이거나 낮추는 결과로 연결. 불안정한 상태
3. Error(SetInput-Input) 미분항의 값이 급격하게 커지거나 작아지는 부분이 발생.

갑작스러운 Setpoint 값 변경은 갑작스런 Error 변화를 유도하고, 그 결과 미분항의 값이 극대화됨. 미분항의 영향으로 갑작스러운 Output 변화를 초래.

드론이 수평을 유지하기 위해서 Setpoint=0. 드론이 수평을 잘 유지하고 있다면 현재 Input=0도.
드론이 약간 기울어져 Input=-0.04라고 가정. Error 0-(-0.04) == 0.04도. 이전 Error 값을 0.08도라고 가정. dError 0.04-0.08 ==-0.04. 센서 입력 주기는 4ms라고 할때 dError = -10.

사용자가 Roll 각도를 변경. Setpoint=3라고 가정. 현재 드론은 수평 상태에 가까워 Input=-0.04라고 가정. Error (3-(-0.04) == 3.04가 됨. 이전 Error 값을 0.08도라고 가정. dError 3.04-0.08 == 2.96이 됨. 센서 입력주기 4ms라고 할때 dError = 740
이 때 dterm이 강해져 output이 달라져 드론이 극도로 불안정한 상태

드론에서 Setpoint가 변하는 상황은 배에서 방향을 변경하는 상황. 현재 진행 방향을 기준으로 우측으로 45도 변경은 Setpoint 변경 목표값 변경을 의미하며 내부적인 의도에 의해 발생.
이 때는 P항이 그 역할을 함. 미분항의 경우는 갑작스런 외력의 변화에 저항하기 위해 사용. Setpoint의 변화는 내부적인 의도를 나타내며, 갑작스런 외력의 변화에 저항하기 위해 필요한 미분항에 적용될 수 없음

dInput = Input - prevInput
// dError = Error - prevError

DTerm = - Kd * (dInput/dt)
// DTerm = Kd * (dError / dt)

$Error = Setpoint - Input$

$\dfrac{dError}{dt} = \dfrac{dSetpoint}{dt} - \dfrac{dInput}{dt}$

$\dfrac{dSetpoint}{dt}=0$이어야 하므로,

$\dfrac{dError}{dt} = -\dfrac{dInput}{dt}$

오차변화율에서 Setpoint가 변하는 경우를 빼면, Error의 미분은 부호가 바뀐 Input의 미분과 같아짐.
이렇게 하면 Setpoint의 변화가 Output 결과에 영향을 주지 못함.

---

3. 드론 각도 보정을 위한 PID 알고리즘

angle_error = target_angle - current_angle
PTerm = Kp * angle_error
ITerm += Ki * angle_error * dt

dAngle = current_angle - previous_angle
Dterm = - Kd * (dAngle / dt)

balancing_force = PTerm + ITerm + DTerm

여기서 dAngle/dt는 각도 변화율 즉, 자이로 센서를 구할 수 있는 각속도이다.

Dterm = -Kd * gyRate

여기서 Kp, Ki, Kd 값은 각도나 회전속도를 증폭 또는 감소시켜 모터의 출력으로 연결.