아이디어

• 각 그래프 별 특징적인 정점을 찾으면 된다.
  • 추가된 정점 $A$: 입력차수 = 0, 출력차수 ≥ 2
  • 막대그래프
    • 다른 두 정점과 달리 경로를 따라갔을 때 끝나는 정점이 있다.
    • 끝 정점: 출력차수 = 0
  • 8자 그래프
    • 8자 모양의 교차점이 있다.
    • 교차점: 입력차수 ≥ 2, 출력차수 2
  • 도넛 그래프
    • 8자 그래프가 아닌 것 중, 경로를 따라갔을 때 제자리로 돌아온다.
    • 또는, 그냥 두 종류가 아닌 나머지 그래프를 도넛 그래프로 취급해도 된다.

코드

Java

import java.util.*;

class Solution {
    static final int M = 1_000_000;
    
    static int[] indeg = new int[M+1];
    static int[] outdeg = new int[M+1];
    
    static Map<Integer, List<Integer>> graph = new HashMap<>();
    
    static int origin, donut, stick, eight;
    
    public int[] solution(int[][] edges) {
        for (int[] e: edges) {
            int v1 = e[0];
            int v2 = e[1];
            outdeg[v1]++;
            indeg[v2]++;
            if (!graph.containsKey(v1)) {
                graph.put(v1, new ArrayList<>());
            }
            graph.get(v1).add(v2);
        }
        
        for (int i=1; i<=M; i++) {
            if (indeg[i] == 0 && outdeg[i] >= 2) {
                origin = i;
                break;
            }
        }
        
        for (int s: graph.get(origin)) {
            // 탐색 시작 지점이 막대 그래프의 끝
            if (outdeg[s] == 0) {
                stick++;
                continue;
            }
            
            int v = graph.get(s).get(0);
            while (true) {
                if (outdeg[v] == 0) {
                    stick++;
                    break;
                }
                if (outdeg[v] == 2) {
                    eight++;
                    break;
                }
                if (v == s) {
                    donut++;
                    break;
                }
                
                v = graph.get(v).get(0);
            }
        }
        
        return new int[] {origin, donut, stick, eight};
    }
}

Python

def solution(edges):
    M = 1_000_000
    
    in_deg = [0]*(M+1)
    out_deg = [0]*(M+1)
    start = 0
    graph = {}
    donut, stick, eight = 0, 0, 0
    
    for v1, v2 in edges:
        out_deg[v1] += 1
        in_deg[v2] += 1
        if v1 in graph:
            graph[v1].append(v2)
        else:
            graph[v1] = [v2]
    
    for i in range(1, M+1):
        # 입력간선이 없고 출력간선이 2 이상 있으면 추가된 간선
        if not in_deg[i] and out_deg[i] >= 2:
            start = i
            break
            
    for s in graph[start]:
        # 탐색 시작 노드가 막대의 마지막
        if out_deg[s] == 0:
            stick += 1
            continue
        
        v = graph[s][0]
        while True:
            # 막대의 끝
            if out_deg[v] == 0:
                stick += 1
                break
            # 8자 그래프의 중심점을 만남
            if out_deg[v] == 2:
                eight += 1
                break
            # 도넛 그래프 돌아옴
            if v == s:
                donut += 1
                break
            
            v = graph[v][0]
        
    
    return [start, donut, stick, eight]

리뷰

• 무조건 탐색을 해야하는 줄 알았는데, 탐색 없이 각 정점 중 입력차수와 출력차수가 같은 것만으로 푸는 풀이가 있어 흥미로웠다.
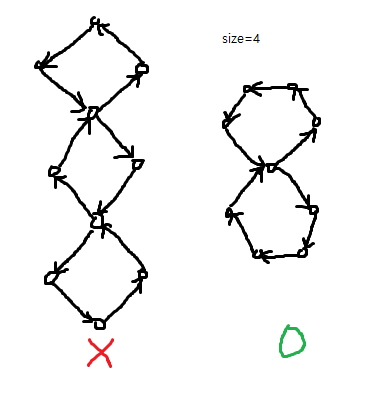
• 8자 그래프에 대한 설명 그림이 오해를 일으킬 수 있다. size = 4일 때는 다음과 같다.