아이디어

• 1층이 밑면이 길이 $n$인 사다리꼴, 평행사변형이 되는 경우를 sadari[n], pyeong[n]이라 하자.
  

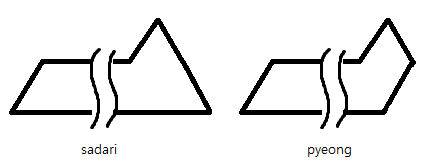
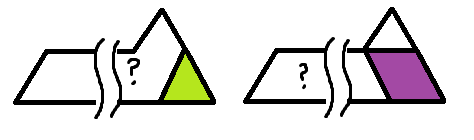
• 이때, sadari[i]는 다음과 같이 2가지 경우가 있다.

  • pyeong[i]의 오른쪽에 삼각형을 추가
  • sadari[i-1]의 오른쪽에 평행사변형(+ 필요하다면 2층) 추가
    

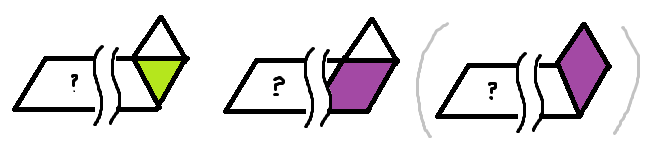
• pyeong[i]는 2층의 여부(tops[i-1] == 1)에 따라 2가지 또는 3가지 경우로 나뉜다.

  • sadari[i]의 오른쪽에 삼각형(+ 필요하다면 2층) 추가
  • pyeong[i-1]의 왼쪽에 평행사변형(+ 필요하다면 2층) 추가
  • 2층이 있을 때, sadari[i]의 오른쪽에 마름모 추가
    

• 위의 관계를 이용해 동적으로 값을 구한다. 최종적으로 구하는 값은 sadari[n+1]이다.

  • $n$은 윗면의 길이이므로 밑면의 길이는 $n+1$이다.

코드

class Solution {
    static final int MOD = 10007;
    
    static int[] sadari, pyeong;
    
    static int n;
    
    static int ans;
    
    public int solution(int n, int[] tops) {
        n = tops.length;
        sadari = new int[n+2];
        pyeong = new int[n+2];
        
        sadari[1] = 1;
        pyeong[1] = tops[0] == 1 ? 3 : 2;
        for (int i=2; i<=n+1; i++) {
            sadari[i] = add(sadari[i-1], pyeong[i-1]);
            pyeong[i] = add(sadari[i], pyeong[i-1]);
            if (i-1 < n && tops[i-1] == 1)
                pyeong[i] = add(pyeong[i], sadari[i]);
        }
        
        return sadari[n+1];
    }
    
    static int add(int a, int b) {
        return (a + b) % MOD;
    }
}

리뷰

• 처음에는 2층이 있는 삼각형 부분에서 사다리꼴을 분할하는 모든 경우의 수를 구하는 방법을 떠올렸으나, 시간복잡도가 $O(2^n)$이 나와 포기했다.
• DP는 아이디어만 제대로 잡으면 코드가 짧아 좋다. 아이디어를 떠올리는 게 제일 문제지만...
• 평행사변형은 영어로 'parallelogram', 사다리꼴은 'tripezoid'라고 한다. 코드가 직관적이지 않아 콩글리시를 좀 썼다.
• 여담으로 2층이 없을 때의 sadari[n]는 $F_{2n-1}$, pyeong[n]은 $F_{2n}$이지만 문제와 큰 관련은 없었다.
  • $\{F_n\}$: 피보나치 수열